Решение. Скорость равномерного движения. B4

Условие

B4. Одно тело, двигаясь равномерно со скоростью 72 км/ч, в течение 10 с прошло такой же путь, какой другое тело прошло за 12,5 с. Определите скорость второго тела.

Решение

υ1 = 72 км/ч = 20 м/с;

t1 = 10 c; t2 = 12,5 c;

s1 = s2

υ2 – ?

При прямолинейном равномерном движении s = Δr = ν·t (1).

1 способ (аналитический). Скорость тела 2 можно найти, используя уравнение (1): υ₂ = s₂/t₂, где t₂ известно. По условию s₂ = s₁, а s₁ = υ₁·t₁, где υ₁ и t₁ известны. Тогда s₂ = υ₁·t₁ и υ₂ = υ₁·t₁/t₂ ; υ₂ = 16 м/с.

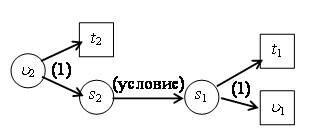
• При данном способе поиск решения упрощается, если строить граф задачи (рис. 1), где величины в кружках – неизвестные, в квадратах – известные; в скобках указаны номера используемых уравнений.

Рис. 1

2 способ (синтетический). Для тела 1 уравнение (1) примет вид s₁ = υ₁·t₁ (2); для тела 2 – s₂ = υ₂·t₂ (3); по условию s₁ = s₂ (4). Получили систему из трех уравнений (2) – (4) с тремя неизвестными. Решим ее.

Из уравнения (3) υ₂ = s₂/t₂ , где, с учетом уравнений (2) и (4), s₂ = υ₁·t₁. Тогда υ₂ = υ₁·t₁/t₂ ; υ₂ = 16 м/с.

Проверка ответа. Два способа решения дали один и тот же ответ.