Решение. Сложение векторов. B1
Содержание
Условие
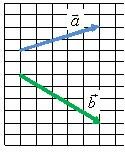
В1. Используя правила треугольника и параллелограмма, постройте векторы суммы и разности векторов \(\vec a\) и \(\vec b\) (рис. 1).
Решение
Решение. Сумма векторов.
Найдем сумму векторов \(\vec a\) и \(\vec b\). Обозначим \(\vec a + \vec b = \vec c\).
Правило треугольника.
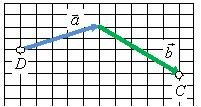
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) нужно переместить вектор \(\vec b\) параллельно самому себе (рис. 2, б) так, чтобы его начало (точка B на рис. 2, а) совпадало с концом вектора \(\vec a\) (точка A на рис. 2, а). Тогда их суммой будет вектор \(\vec c\) (рис. 2, г), начало которого совпадает с началом вектора \(\vec a\) (точка D на рис. 2, в), а конец — с концом вектора \(\vec b\) (точка C на рис. 2, в).



Правило параллелограмма.
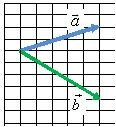
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\vec a\) и \(\vec b\) находились в одной точке (рис. 3, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 3, б). Тогда их суммой будет вектор \(\vec c\) (рис. 3, в), начало которого совпадает с общим началом векторов (точка A на рис. 3, б), а конец — с противоположной вершиной параллелограмма (точка В на рис. 3, б).


Решение. Разность векторов.
Для того чтобы найти \(\vec a - \vec b\) найдем \(\vec a + (- \vec b)\). Обозначим \(\vec a + (- \vec b) = \vec c\)
Правило треугольника.
Для того чтобы сложить два вектора \(\vec a\) и \(-\vec b\) нужно переместить вектор \(-\vec b\) параллельно самому себе (рис. 4, б) так, чтобы его начало (точка B на рис. 4, а) совпадало с концом вектора \(\vec a\) (точка A на рис. 4, а). Тогда их суммой будет вектор \(\vec c\) (рис. 4, г), начало которого совпадает с началом вектора \(\vec a\) (точка D на рис. 4, в), а конец — с концом вектора \(-\vec b\) (точка C на рис. 4, в).




Правило параллелограмма.
Для того чтобы сложить два вектора \(\vec a\) и \(-\vec b\) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\vec a\) и \(-\vec b\) находились в одной точке (рис. 5, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 5, б). Тогда их суммой будет вектор \(\vec c\) (рис. 5, в), начало которого совпадает с общим началом векторов (точка A на рис. 5, б), а конец — с противоположной вершиной параллелограмма (точка В на рис. 5, б).



