Решение. Третий закон Ньютона. B4

Условие

B4. Сравните модули ускорений двух стальных шаров во время столкновения, если радиус первого шара в 2 раза больше радиуса второго.

Решение

Два шара;

взаимодействие;

R1 = 2R2;

\(~\frac{a_1}{a_2}\) – ?

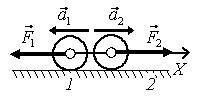
Направим ось 0Х по направлению полученного ускорения второго шара. Сила удара, с которой первый шар действует на второй, направлена вдоль этой оси. Тогда сила удара, с которой второй шар действует на первый, и ускорение первого шара будут направлены против этой оси (рис. 1). Ускорение и сила связаны соотношением \(~a_x = \frac{F_x}{m}\) (1).

Для первого шара уравнение (1) примет вид \(~a_{1x} = \frac{F_{1x}}{m_1}\) , для второго шара – \(~a_{2x} = \frac{F_{2x}}{m_2}\) , где a_1x = –a₁, F_1x = –F₁, a_2x = a₂, F_2x = F₂ (рис. 1), m₁ = ρ₁∙V₁, m₂ = ρ₂∙V₂, ρ₁ = ρ₂ – плотность стали, \(~V_1 = \frac{4}{3} \pi \cdot R^3_1 , V_2 = \frac{4}{3} \pi \cdot R^3_2\) . При взаимодействии двух шаров F_1x = –F_2x. Так как F_1x = –F₁, F_2x = F₂, то F₁ = F₂. Тогда

\(~-a_1 = \frac{-F_1}{m1} ; a_2 = \frac{F_2}{m2} ; \frac{a_1}{a_2} = \frac{F_1}{m_1} \cdot \frac{m_2}{F_2} = \frac{m_2}{m_1} = \frac{\rho_2 \cdot \frac{4}{3} \pi \cdot R^3_2}{\rho_1 \cdot \frac{4}{3} \pi \cdot R^3_1} = \frac{R^3_2}{R^3_1} = \frac{R^3_2}{(2R_2)^3} = \frac{1}{8}\) .

Ускорение второго шарика в 8 раз больше ускорения первого.

Рис. 1