Решение. Уравнения движения. B2

Условие

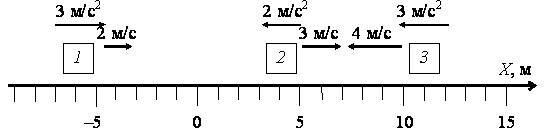
B2. Используя данные рисунка 1:

а) найдите координаты тел, их проекции начальных скоростей и ускорений;

б) запишите уравнения проекций скорости, перемещения, координаты (движения) для каждого тела;

в) определите проекции скорости, перемещения и координату каждого тела через 3 с;

г) найдите расстояние через 3 с: между 1-м и 2-м телами; между 2-м и 3-м телами;

д) определите, когда проекции скорости тел будут равны 0 м/с.

Рис. 1

Решение

а) Найдем координаты тел, их проекции начальных скоростей и ускорений из рисунка:

для 1-го тела: x₁₀ = –6 м, υ_10x = 2 м/с, a_1x = 3 м/с²;

для 2-го тела: x₂₀ = 4 м, υ_20x = 3 м/с, a_2x = –2 м/с²;

для 3-го тела: x₃₀ = 11 м, υ_30x = –4 м/с, a_3x = –3 м/с².

б)

Уравнение проекции скорости \(~\upsilon_x = \upsilon_{0x} + a_x \cdot t\).

Для 1-го тела: υ_1x = υ_10x + a_1x·t, где υ_10x = 2 м/с, a_1x = 3 м/с² (см. п. а). Тогда υ_1x = 2 + 3·t.

Для 2-го тела: υ_2x = υ_20x + a_2x·t, где υ_20x = 3 м/с, a_2x = –2 м/с². Тогда υ_2x = 3 – 2·t.

Для 3-го тела: υ_3x = υ_30x + a_3x·t, где υ_30x = –4 м/с, a_3x = –3 м/с². Тогда υ_3x = –4 – 3·t.

Уравнение проекции перемещения \(~\Delta r_x = \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\) .

Для 1-го тела\[~\Delta r_{1x} = \upsilon_{10x} \cdot t + \frac{a_{1x} \cdot t^2}{2}\] , где υ_10x = 2 м/с, a_1x = 3 м/с². Тогда Δr_1x = 2·t + 1,5·t².

Для 2-го тела\[~\Delta r_{2x} = \upsilon_{20x} \cdot t + \frac{a_{2x} \cdot t^2}{2}\] , где υ_20x = 3 м/с, a_2x = –2 м/с². Тогда Δr_2x = 3·t – t².

Для 3-го тела\[~\Delta r_{3x} = \upsilon_{30x} \cdot t + \frac{a_{3x} \cdot t^2}{2}\] , где υ_30x = –4 м/с, a_3x = –3 м/с². Тогда Δr_3x = –4·t – 1,5·t².

Уравнение координаты (движения) \(~x = x_0 + \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\) .

Для 1-го тела\[~x_1 = x_{10} + \upsilon_{10x} \cdot t + \frac{a_{1x} \cdot t^2}{2}\] , где x₁₀ = –6 м, υ_10x = 2 м/с, a_1x = 3 м/с². Тогда x₁ = –6 + 2·t + 1,5·t².

Для 2-го тела\[~x_2 = x_{20} + \upsilon_{20x} \cdot t + \frac{a_{2x} \cdot t^2}{2}\] , где x₂₀ = 4 м, υ_20x = 3 м/с, a_2x = –2 м/с². Тогда x₂ = 4 + 3·t – t².

Для 3-го тела\[~x_3 = x_{30} + \upsilon_{30x} \cdot t + \frac{a_{3x} \cdot t^2}{2}\] , где x₃₀ = 11 м, υ_30x = –4 м/с, a_3x = –3 м/с². Тогда x₃ = 11 – 4·t – 1,5·t².

в)

Проекция скорости через 3 с.

1-го тела: так как υ_1x = 2 + 3·t, то υ_1x(3 с) = 2 + 3·3 = 11 (м/с);

2-го тела: так как υ_2x = 3 – 2·t, то υ_2x(3 с) = 3 – 2·3 = –3 (м/с)

3-го тела: так как υ_3x = –4 – 3·t, то υ_3x(3 с) = –4 – 3·3 = –13 (м/с).

Проекция перемещения через 3 с.

1-го тела: так как Δr_1x = 2·t + 1,5·t², то Δr_1x(3 с) = 2·3 + 1,5·(3)² = 19,5 (м);

2-го тела: так как Δr_2x = 3·t – t², то Δr_2x(3 с) = 3·3 – (3)² = 0;

3-го тела: так как Δr_3x = –4·t – 1,5·t², то Δr_3x(3 с) = –4·3 – 1,5·(3)² = –25,5 (м).

Координата через 3 с.

1-го тела: так как x₁ = –6 + 2·t + 1,5·t², то x₁(3 с) = –6 + 2·3 + 1,5·(3)² = 13,5 (м);

2-го тела: так как x₂ = 4 + 3·t – t², то x₂(3 с) = 4 + 3·3 – (3)² = 4 (м);

3-го тела: так как x₃ = 11 – 4·t – 1,5·t², то x₃ = 11 – 4·3 – 1,5·(3)² = –14,5 (м).

г)

Расстояние между n-ым и m-ым телами через t с:

l = |x_m(t с) – x_n(t с)|, где x_m(t с) – координата m-ого тела через t с; x_n(t с) – координата n-ого тела через t с.

Расстояние через 3 с между 1-м и 2-м телами: l_1-2 = |x₁(3 с) – x₂(3 с)|, где x₁(3 с) = 13,5 м; x₂(3 с) = 4 м. Тогда l_1-2 = |13,5 м – 4 м| = 9,5 (м).

Расстояние через 3 с между 2-м и 3-м телами: l_2-3 = |x₂(3 с) – x₃(3 с)|, где x₂(3 с) = 4 м; x₃(3 с) = –14,5 м. Тогда l_2-3 = |4 м – (–14,5 м)| = 18,5 (м).

д) Время, когда проекция скорости тела будет равна 0, можно найти следующим образом\[~\upsilon_x = \upsilon_{0x} + a_x \cdot t\] = 0.

Для 1-го тела: υ_1x = 2 + 3t = 0; 3t = –2; t = –2/3 ≈ -0,67 ≈ –0,7 (с), (знак «–» указывает, что это событие произошло до начала отсчета).

Для 2-го тела: υ_2x = 3 – 2t = 0; t = 1,5 (с).

Для 3-го тела: υ_3x = –4 – 3t = 0; t ≈ –1,3 (с).