Решение. Уравнения движения. B6
Условие
B6. По прямолинейной дороге в одном направлении едут велосипедист со скоростью 36 км/ч и мотоциклист со скоростью 72 км/ч. В начальный момент времени расстояние между ними было 250 м. Когда и где мотоциклист догонит велосипедиста?
Решение
В задаче два тела: 1) велосипедист; 2) мотоциклист, – которые движутся прямолинейно и равномерно (по умолчанию).
Задачу решим, используя уравнение движения \(~x = x_0 + \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\) , где ax = 0. Тогда \(~x = x_0 + \upsilon_{0x} \cdot t\) (1).
Ось 0Х направим в сторону движения. Возможно два варианта расположения велосипедиста и мотоциклиста.
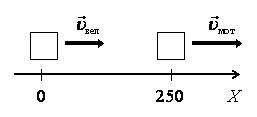
1 вариант. За тело отсчета примем положение велосипедиста (рис. 1 а).
Так как скорость велосипедиста меньше скорости мотоциклиста, то мотоциклист никогда не догонит велосипедиста.
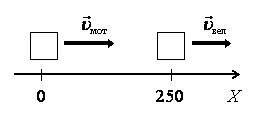
2 вариант. За тело отсчета примем положение мотоциклиста (рис. 1 б). Запишем уравнение (1) для тела 1\[~x_1 = x_{10} + \upsilon_{1x} \cdot t\]; для тела 2\[~x_2 = x_{20} + \upsilon_{2x} \cdot t\], где x10 = 250 м; υ1x = υвел = 36 км/ч = 10 м/с; x20 = 0; υ2x = υмот = 72 км/ч = 20 м/с. Тогда x1 = 250 + 10t; x2 = 20t.
Так как тела встретились, то x1(tвстр) = x2(tвстр) или 250 + 10tвстр = 20tвстр. Решим полученное уравнение: 250 = 10tвстр; tвстр = 25 (с).
Место встречи x1(25 с) = 500 (м) (можно было и x2(25 с) = 500 (м)).
Ответ. Мотоциклист догонит велосипедиста через 25 с, проехав 500 м.