Решение. Уравнения движения. B8

Условие

B8. Заданы уравнения движения для пяти тел. По этим уравнениям определите начальные координаты, проекции начальных скоростей и ускорений тел. Перерисуйте рисунок 1 и расставьте на нем тела соответственно их начальным координатам, обозначьте их начальные скорости и ускорения (модуль и направление).

x₁ = – 60 – 8t + 2,5t²;

x₂ = 10t' – 40;

x₃ = (10 – t)²;

x₄ = –10t –2,5t² + 60;

x₅ = (6 – 0,4t²)·5.

Рис. 1

Решение

Уравнение движения \(~x = x_0 + \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\) .

Перепишем уравнения движения для тел 3 и 5 в стандартный вид\[~x_3 = (10 - t)^2 = 100 - 20t + t^2; x_5 = (6 - 0,4t^2) \cdot 5 = 30 - 2t^2\] .

Начальная координата x₀ – величина, стоящая в уравнении движения без t; проекция начальной скорости υ_0x – величина, стоящая при t; проекция ускорения a_x – величина, стоящая при \(~\frac{t^2}{2}\) , или удвоенная величина, стоящая при t².

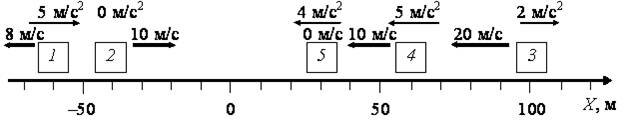
Тогда для 1-го тела x₁: = – 60 – 8t + 2,5t²: x₁₀ = –60 м, υ_10x = –8 м/с, a_1x = 5 м/с²;

для 2-го тела x₂: = 10t – 40: x₂₀ = –40 м, υ_20x = 10 м/с, a_2x = 0;

для 3-го тела x₃: = 100 – 20t + t²: x₃₀ = 100 м, υ_30x = –20 м/с, a_3x = 2 м/с²;

для 4-го тела x₄: = –10t –2,5t² + 60: x₄₀ = 60 м, υ_40x = –10 м/с, a_4x = –5 м/с²;

для 5-го тела x₅: = 30 – 2t²: x₅₀ = 30 м, υ_50x = 0, a_5x = –4 м/с².

Расположение тел указано на рисунке 2.

Рис. 2