Решение. Условия равновесия тел. C1

Условие

С1. Два человека несут доску. Как разнятся усилия, прилагаемые одним и другим в зависимости от точек хвата и высоты подъёма той самой доски? Если скажем один идет впереди и несет её на плече, а другой идёт сзади и несёт её под мышкой. Кому тяжелее?

(Вопрос задал посетитель форума www.alsak.ru Димка).

Решение

Построим модель задачи. Пусть доска имеет массу m и она однородная, тонкая (тогда ее центр тяжести будет находиться в середине доски); высота первой опоры (высота плеча первого человека) равна h₁; высота второй опоры – h₂; расстояние вдоль доски от центра тяжести до первой опоры – l₁; расстояние от центра тяжести до второй опоры – l₂. При наклоне скольжению доски препятствует сила трения, причем угол наклона доски не должен превышать arctg α (условие проскальзывания).

Усилия, которые должен приложить человек, будут равняться равнодействующей сил N и F_tr:

\(F = \sqrt{N^2 + F_{tr}^2}= \sqrt{N^2 + {\mu \cdot N}^2}= N \cdot \sqrt{1 + \mu^2}\).

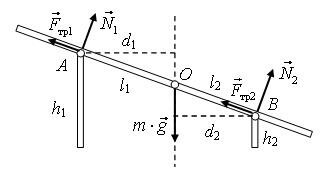
Изобразим действующие силы на доску (рис. 1, а).

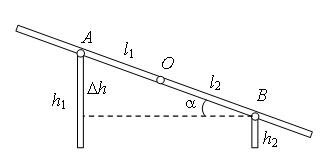
Выполним предварительные расчеты (рис. 1, б). Угол наклона доски к горизонту .

\( \sin \alpha = \frac{\Delta h}{l_1 + l_2}= \frac{h_1 - h_2}{l_1 + l_2}; \cos \alpha = \frac{\sqrt{{l_1 + l_2}^2 - \Delta h}}{l_1 + l_2}= \sqrt{1 - \frac{h_1 - h_2}{l_1 + l_2}}\).

Плечи равны

\(d_1 = l_1 \cdot \cos \alpha; d_2 = l_2 \cdot \cos \alpha\).

Найдем значения N₁ и N₂. Учтем для этого, что это тело без закрепленной оси вращения. Условие равновесия доски относительно точки А:

\( m \cdot g \cdot d_1 - N_2 \cdot (l_1 + l_2) = 0\).

Тогда

\( N_2 = \frac{m \cdot g \cdot d_1}{l_1 + l_2} = \frac{m \cdot g \cdot l_1 \cdot \cos \alpha}{l_1 + l_2}\).

Аналогично, рассматривая условие равновесия доски относительно точки В, получаем

\( N_1 = \frac{m \cdot g \cdot d_2}{l_1 + l_2} = \frac{m \cdot g \cdot l_2 \cdot \cos \alpha}{l_1 + l_2}\).

Анализ уравнения \( \left( N_1 = \frac{m \cdot g \cdot \cos \alpha}{\frac {l_1}{l_2}+1} \right )\) показывает, что давление доски на человека, который находится в точке А, уменьшается при увеличении l₁ (человек должен отходить ближе к краю), при уменьшении l₂ и при увеличении (?!) угла наклона доски (не забывайте, что доска может начать скользить, и тогда придется ее еще удерживать от скольжения).

а

а

Рис. 1

Если полученные результаты противоречат реальной жизни, то следует, что в модели задачи что-то важное мы не учли. Думайте.