Слободянюк А.И. Физика 10/1.3
§1. Описание положения тела в пространстве
1.3. Относительные и инвариантные величины
Мы показали, что при переходе из одной системы в другую координаты точки изменяются (координаты относительны). Помимо относительных величин (зависящих от системы координат) имеются величины независящие от системы координат (такие величины называются инвариантными). Примером такой величины является расстояние между двумя точками. Действительно, пусть на плоскости (рис.4) расположены две точки: A1 с координатами (x1,y1) и A2 с координатами (x2,y2).
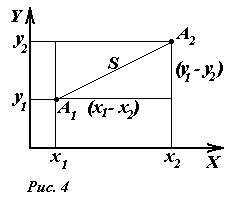
Тогда на основании теоремы Пифагора расстояние между точками может быть вычислено по формуле
При переходе в любую другую систему отсчета (при неизменной единице длины) расстояние, вычисленное по формуле (4), остается неизменным. Например, при сдвиге начала отсчета, описываемом уравнениями (1), все четыре координаты изменятся, но разности одноименных координат, а, следовательно, и расстояние останутся неизменными (инвариантными). Можно указать и другие геометрические инвариантные величины – углы между отрезками, площади и объемы фигур и др. Особенно отметим, что соотношения, записанные в векторной форме, остаются неизменными при преобразованиях координат. Так, например, скалярное произведение[1] двух векторов не зависит от выбора системы координат. В частном случае, скалярное произведение вектора на самого себя равно квадрату длины вектора. Поэтому формула (4) в векторной форме имеет вид
Поиск инвариантных величин, не изменяющихся при преобразованиях координат, представляет большой интерес, а многие физические теории и формулируются в терминах инвариантных величин.
Задание для самостоятельной работы
1. В полярной системе координат положение точки A на плоскости задается с помощью а) расстояния r до начала координат O, б) угла φ, который образует отрезок OA с осью X.
Установите связь между полярными (r,φ) и декартовыми координатами точки.
Выразите расстояние между двумя точками через их полярные координаты.
Обсуждая вопрос об описании положения тела в пространстве, мы стыдливо умолчали о том, что не определили понятия «тело». Фактически речь шла о геометрических точках пространства. Любой реальный объект имеет конечные геометрические размеры и определенную форму. Кроме того, реальные тела обладают множеством иных характеристик - массой, температурой, цветом и так далее. Полностью описать все свойства реальных тел, все физические процессы в рассматриваемых телах невозможно из-за их бесконечного многообразия. Поэтому, рассматривая те или иные явления необходимо отвлечься, «забыть» на время, пренебречь некоторыми характеристиками тел и явлений, иными словами, построить модель явления, модель тела. Какими свойствами тела можно в данных условиях пренебречь зависит от конкретной физической задачи, конкретной цели физического исследования.
Примечания
- ↑ Напомним, результатом скалярного произведения двух векторов \(~\vec A\) и \(~\vec B\) называется число c , равное произведению модулей векторов на косинус угла α между ними\[~c = \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot \cos \alpha\] .
