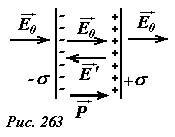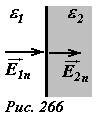Слободянюк А.И. Физика 10/10.6

Содержание книги

Предыдующая страница

§10. Проводники и диэлектрики в электростатическом поле

10.6 Описание электрического поля в диэлектриках.

Описание электрического поля в диэлектриках, помимо проблем, рассмотренных при расчете полей в присутствии проводников, усложняется тем, что внутри диэлектриков могут возникать объемные поляризационные заряды. Поэтому мы в состоянии рассмотреть только простейшие задачи, связанные с описанием полей в присутствии диэлектриков.

Прежде всего, мы ограничим рассмотрение однородными и изотропными диэлектриками, то есть веществами, у которых поляризуемость одинакова во всех точках и не зависит от направления поля. Кроме того, будем рассматривать электрические поля только простейшей конфигурации.

Заметим, что среди диэлектриков существуют такие кристаллические диэлектрики, в которых поляризуемость зависит от направления поля (анизотропия). Качественно понять такую зависимость можно – смещение зарядов различно в различных направлениях. В таких диэлектриках направление вектора поляризации может не совпадать с направлением вектора напряженности электрического поля.

Пусть во внешнее однородное электрическое поле помещена плоскопараллельная пластина толщиной h, изготовленная из однородного диэлектрика, причем силовые линии электрического поля перпендикулярны граням пластины.

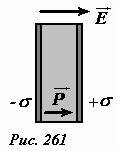
Под действием электрического поля диэлектрик поляризуется, то есть происходит смещение положительных и отрицательных зарядов. Схематически картину поляризации можно представить следующим образом. Мысленно разделим пластину на две – однородно заряженные (положительно и отрицательно) вложенные друг в друга (рис.261). Объемные плотности зарядов этих воображаемых пластин равны по модулю. Поэтому когда платины полностью вложены одна в другую, то суммарная объемная плотность заряда равна нулю. При наложении внешнего однородного поля происходит малое смещение этих пластин друг относительно друга. В области их перекрытия объемный заряд по-прежнему отсутствует, а там где они расходятся, появляются нескомпенсированные заряды. Так как смещения зарядов крайне малы, то можно считать, что на поверхностях появляются поверхностные заряды, поверхностную плотность которого обозначим σ. Заметим, что в данном случае поляризационные заряды не создают электрического поля вне пластины, поэтому здесь поле остается неизменным.

Свяжем поверхностную плотность индуцированных поляризационных зарядов с величиной вектора поляризации диэлектрика. Для этого выделим в пластине цилиндр, основания которого (площадью ΔS) расположены на гранях пластины. С одной стороны, по определению вектора поляризации P, дипольный момент выделенного цилиндра равен произведению модуля вектора поляризации на объем цилиндра ΔV = hΔS

\(~p = P \Delta V = P h \Delta S\) ,

а с другой, по определению дипольного момента, эта же величина равна произведению заряда основания \(q = \sigma \Delta S\), на расстояние между зарядами h

\(~p = q h = \sigma \Delta S h\) .

Из сравнения этих выражений следует замечательный результат: поверхностная плотность поляризационных зарядов равна модулю вектора поляризации диэлектрика:

\(~\sigma = P\) . (1)

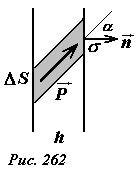
В общем случае вектор поляризации диэлектрика может быть направлен под некоторым углом α к поверхности. Также выделим внутри пластины наклонный цилиндр, основания которого находятся на гранях пластины, а образующие параллельны вектору поляризации \(~\vec P\). В этом случае запишем нормальную к поверхности составляющую дипольного момента выделенного цилиндра в двух формах:

-по определению вектора поляризации

\(~p_n = P_n \Delta V = P \cos \alpha h \Delta S\) ;

- по определению дипольного момента

\(~p_n = q h = \sigma \Delta S h\) .

Из сравнения этих выражений следует, что поверхностная плотность поляризационных зарядов равна нормальной составляющей вектора поляризации диэлектрика:

\(~\sigma = P_n\) . (2)

Вернемся к расчету поля внутри диэлектрической пластины. Напряженность электрического поля внутри пластины равно сумме напряженностей внешнего поля \(~\vec E_0\) и поля, создаваемого поляризационными зарядами \(~\vec E'\) (рис. 263)

\(~\vec E = \vec E_0 + \vec E'\) . (3)

Напряженность поля поляризационных зарядов выражается через поверхностную плотность зарядов σ

\(~E' = \frac{\sigma}{\varepsilon_0}\) ,

которая в свою очередь равна модулю вектора поляризации \(~\sigma = P\). Поляризация среды определяется полем внутри нее, то есть величиной суммарной напряженности \(~P = \chi \varepsilon_0 E\) . Подставляя значение напряженности E&rsquo в выражение (3), записанное в проекции на направление внешнего поля получим

\(~E = E_0 - E' = E_0 - \frac{\sigma}{\varepsilon_0} = E_0 - \frac{P}{\varepsilon_0} = E_0 - \frac{\chi \varepsilon_0 E}{\varepsilon_0}\) . (4)

Обратите внимание, искомая величина напряженности поля внутри диэлектрика входит в обе части уравнения (4). Яркая иллюстрация «зацикленности» - поле внутри зависит от индуцированных зарядов, индуцированные заряды зависят от поля внутри. Однако в данном простейшем случае задача определения поля оказалась разрешимой.

Из уравнения (4) получаем

\(~E = \frac{E_0}{1 + \chi} = \frac{E_0}{\varepsilon}\) . (5)

Из записанных соотношений также можно выразить поверхностную плотность поляризационных зарядов

\(~\sigma = P = \chi \varepsilon_0 E = \frac{\varepsilon - 1}{\varepsilon} \varepsilon_0 E_0\) . (6)

В этих соотношениях обозначено \(\varepsilon = 1 + \chi\). Таким образом, поляризационные заряды уменьшают поле внутри диэлектрика в (1 + χ) раз по сравнению с внешним полем. Величина ε = 1 + χ называется диэлектрической проницаемостью вещества. Именно эта величина выступает в качестве основной характеристики электрических свойств веществ и чаще всего приводится в справочниках физических величин.

Диэлектрическая проницаемость веществ может изменяться в широких пределах

– так для газов она отличается от единицы на величину порядка 10^-4 - 10^-6 (поэтому часто диэлектрическими свойствами газов пренебрегают);

- для жидких и твердых неполярных диэлектриков она составляет несколько единиц (например, для керосина ε = 2);

- для полярных диэлектриков несколько десятков единиц (например, для воды ε = 81);

- есть вещества, для которых диэлектрическая проницаемость составляет величины порядка десятков и сотен тысяч (эти вещества называются сегнетоэлектриками).

Диэлектрическая проницаемость вещества показывает, во сколько раз это вещество уменьшает напряженность электрического поле, при условии, что силовые линии поля перпендикулярны поверхности диэлектрика. Конечно, это уменьшение связано с тем, что на поверхности диэлектрика возникают поляризационные заряды, поле которого направлено противоположно внешнему полю, породившему эти заряды.

Особо подчеркнем, что поле внутри диэлектрического тела зависит от:

- внешнего поля \(~\vec E_0\) ;

- диэлектрической проницаемости вещества;

- формы тела.

Утверждение о том, что диэлектрик всегда уменьшает поле в ε раз, мягко говоря, не всегда справедливо, оно верно тогда когда силовые линии перпендикулярны границам тела, или если эти границы находятся так далеко, что полем поляризационных зарядов можно пренебречь.

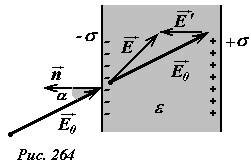
Пусть теперь внешнее однородное поле \(~\vec E_0\) направлено под некоторым углом α к нормали поверхности пластины (рис. 264). Напряженность поля внутри пластины и в этом случае сумме напряженностей внешнего поля \(~\vec E_0\) и поля, создаваемого поляризационными зарядами \(~\vec E'\)

\(~\vec E = \vec E_0 + \vec E'\) .

Напряженность поля создаваемого поляризационными зарядами \(~\vec E'\) направлено перпендикулярно поверхности пластин (не совпадает с направлением внешнего поля \(~\vec E_0\)), поэтому вектор напряженности электрического поля внутри пластины направлен под другим углом к поверхности пластины.

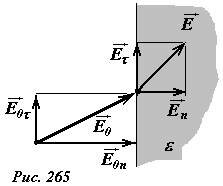
Для определения поля разложим векторы напряженности полей вне и внутри пластины на нормальные (перпендикулярные к поверхности) \(~\vec E_{0n}, \vec E_n\) и тангенциальные (параллельные поверхности) \(~\vec E_{0 \tau}, \vec E_{\tau}\) составляющие (рис. 265). Согласно принципу суперпозиции эти компоненты поля можно рассматривать независимо.

Случай нормальных составляющих мы уже рассмотрели и показали, что для напряженностей полей выполняется соотношение \(~E_n = \frac{E_{0n}}{\varepsilon}\), которое можно переписать в виде

\(~E_{0n} = \varepsilon \cdot E_n\) . (7)

Так как поляризационные заряды создают поле, вектор напряженности которого направлен перпендикулярно поверхности, то тангенциальные составляющие полей вне и внутри пластины будут равны

\(~E_{0\tau} = E_{\tau}\) . (8)

Соотношения (7) и (8) определяют законы изменения векторов напряженностей полей на границе диэлектрика (задают граничные условия). Они играют важную роль при расчетах полей в присутствии диэлектриков.

Выразим модуль вектора напряженности поля внутри диэлектрика

\(~E = \sqrt{E^2_n + E^2_{\tau}} = \sqrt{\left ( \frac{E_0 \cos \alpha}{\varepsilon} \right)^2 + (E_0 \sin \alpha)^2} = \frac{E_0}{\varepsilon} \sqrt{\cos^2 \alpha + \varepsilon^2 \sin^2 \alpha}\) .

Как видите, вектор напряженности поля внутри диэлектрика не только не совпадает по направлению с напряженностью внешнего поля, но и его модуль зависит от угла, между напряженностью внешнего поля и вектором нормали к поверхности диэлектрика.

Задания для самостоятельной работы.

1. Покажите, что на плоской границе двух диэлектриков с диэлектрическим проницаемостями ε₁ и ε₂ для нормальных составляющих векторов напряженностей полей выполняется граничное условие \(~\varepsilon_1 E_{1n} = \varepsilon_2 E_{2n}\) (рис. 266).
2. Найдите соотношение между углами, которые образуют векторы напряженностей полей с нормалью к границе раздела двух диэлектриков.

Если проводящее тело находится внутри диэлектрика, то на границе проводника и диэлектрика возникают поляризационные заряды, которые уменьшают поле внутри диэлектрика. Найдем поверхностную плотность этих зарядов. Пусть в некоторой точке поверхности проводника поверхностная плотность заряда равна σ₀, тогда напряженность поля, создаваемого зарядами на проводнике определяется выражением \(~E_0 = \frac{\sigma_0}{\varepsilon_0}\) . Это поля выступает в качестве внешнего по отношению к диэлектрику и направлено перпендикулярно границе диэлектрика. Поэтому согласно формуле (6) поверхностная плотность поляризационных зарядов на диэлектрике равна

\(~\sigma' = \frac{\varepsilon - 1}{\varepsilon} \varepsilon_0 E_0 = \frac{\varepsilon - 1}{\varepsilon} \sigma_0\) .

Понятно, что эти заряды противоположны по знаку зарядам на проводнике, поэтому суммарная поверхностная плотность заряда в данной точке границы равна

\(~\sigma_0 - \sigma' = \frac{\sigma_0}{\varepsilon}\) .

Вот еще одно явное объяснение уменьшения поля в диэлектрике – на границе проводника и диэлектрика возникают поляризационные заряды противоположного знака, при этом суммарный поверхностный заряд уменьшается в ε раз, соответственно во всех точках внутри диэлектрика поле также уменьшается во столько же раз (конечно, если пренебречь полем зарядов, возникающих на других границах диэлектрика).

Если два небольших заряженных тела (которые можно считать точечными зарядами) находятся внутри бесконечного диэлектрика, то сила взаимодействия между ними уменьшается, по сравнению с силой взаимодействия в вакууме. На границе раздела заряженных тел и диэлектрика возникают поляризационные заряды, которые частично экранируют поля, создаваемые точечными зарядами. Как мы показали, напряженность поля, создаваемого одним из зарядов, уменьшается в ε раз, по сравнением с полем в вакууме. Поэтому сила, действующая на второе тело, также уменьшается в ε раз. Заметьте, что речь идет о силе, действующей на само заряженное тело, без учета сил, действующих на поляризационные заряды, возникшие вблизи этого тела. Ведь эти поляризационные заряды «привязаны» к диэлектрику, а не к рассматриваемому телу. Поэтому сила взаимодействия двух точечных зарядов, находящихся в однородном бесконечном диэлектрике рассчитывается по формуле

\(~F = \frac{q_1 q_2}{4 \pi \varepsilon_0 \varepsilon r^2}\) .

В некоторых учебных и справочных пособиях по физике именно эту формулу приводят в качестве формулировки закона Кулона. Однако, такое расширение закона Кулона нельзя признать удовлетворительным. Во-первых, эта формула получена как следствие применения законов электрического поля и свойств веществ, во-вторых, ее применение требует значительных оговорок – диэлектрик должен быть бесконечным, однородным, для него должна выполняться линейная связь между напряженностью поля и поляризацией диэлектрика. Далее, диэлектрическая проницаемость является усредненной характеристикой вещества, она никоим образом не учитывает атомную структуру строения материи – очень интересный вопрос: «чему равна сила взаимодействия между двумя электронами, находящимися в воде?», ведь размеры электрона намного меньше размеров молекулы воды. Поэтому разумно формулировать, как постулат (подтверждаемый экспериментально) закон Кулона, как закон взаимодействия точечных зарядов в вакууме, а влияние среды на взаимодействие заряженных тел рассматривать отдельно, и полученные результаты рассматривать как следствие из закона Кулона и электрических свойств среды.

Следующая страница