Слободянюк А.И. Физика 10/12.12
§12. Постоянное магнитное поле
12.12 Циркуляция вектора индукции. Теорема о циркуляции магнитного поля.
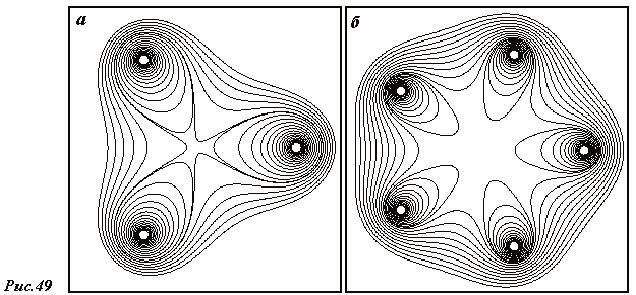
Силовые линии магнитного поля являются замкнутыми кривыми, поэтому картины силовых линий магнитного поля напоминают линии тока жидкости, движущейся с завихрениями. Посмотрите еще раз на приведенные ранее картины силовых линий магнитного поля – сплошные вихри. На рис. 49 показаны еще два примера силовых линий магнитного поля, созданного длинными параллельными проводниками (на рис. 49.а – их три, а на рис. 49.б – пять), по которым протекают равные токи.
Для математического описания таких полей удобно использовать понятие циркуляции вектора.
Точнее следует сказать, что знание циркуляции необходимо для описания любого векторного поля: напомним, любое векторное поле определяется однозначно, если известны теоремы о потоке и циркуляции векторов этого поля. Другое дело, что в электростатическом поле циркуляция вектора по любому контуру равна нулю, поэтому электростатическое поле является потенциальным и для него оказывается возможным ввести такую важную физическую характеристику как потенциал поля. Для магнитного поля циркуляция не имеет явного физического смысла, а является весьма полезной вспомогательной математической величиной.
Определение циркуляции вектора магнитной индукции, аналогично определению циркуляции любого векторного поля.
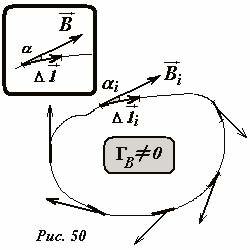
Рассмотрим произвольную замкнутую линию (не обязательно, чтобы это была силовая линия). Выделим на этой линии малый участок, определяемый вектором \(~\Delta \vec l\) (рис. 50). Пусть вектор индукции магнитного поля на этом участке равен \(~\vec B\) , вычислим скалярное произведение этих векторов
где α - угол между вектором индукции и касательным вектором к выбранной линии (он совпадает с выделенным малым участком \(~\Delta \vec l\)). Далее разобьем всю замкнутую линию (Рис. 50) на малые участки \(~\Delta \vec l_i\) , на каждом из которых вычислим скалярное произведение \(~\Delta \Gamma_{Bi} = \vec B_i \cdot \Delta \vec l_i = B_i \Delta l_i \cos \alpha_i\) , и просуммируем [1] их по всем участкам замкнутой линии (контура)
Построенная таким образом, математическая конструкция называется циркуляцией вектора магнитной индукции по заданному контуру L. Ее величина может быть как положительной, так и отрицательной, ее знак определяется произвольным выбором направления обхода контура, но, как обычно, положительным принимается направление обхода против часовой стрелки.
Понятно, что циркуляция магнитного поля может отличаться от нуля. Например, если в качестве произвольного контура выбрать замкнутую силовую линию, то при ее обходе на всех участках вектор индукции будет совпадать по направлению с направлением касательной, как было сказано ранее, «все время будем плыть по течению».
Теперь нам необходимо установить теорему, позволяющую установить циркуляцию вектора индукции. Отметим, что эта теорема является прямым следствием закона Био-Саварра-Лапласа, можно сказать, иной математической формулировкой этого физического закона. Не будем заниматься строгим доказательством теоремы, а проиллюстрируем ее простым примером.
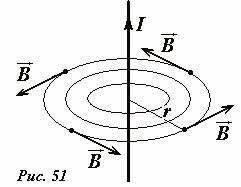
Пусть магнитное поле создается длинным прямым проводником, по которому протекает электрический ток силой I. Индукцию такого поля мы рассчитали: силовые линии являются концентрическим окружностями с центрами на проводнике (Рис. 51). Легко подсчитать циркуляцию вектора индукции (1) по контуру, совпадающему с одной из силовых линий (например, радиуса r). Действительно, на любом участке этого контура вектор индукции направлен по касательной (поэтому все αi = 0), а модуль вектора индукции постоянен и равен \(~B_i = \frac{\mu_0 I}{2 \pi r}\) , поэтому суммирование в формуле (1) сводится к вычислению длин малых отрезков окружности (после недолгих размышлений можно сообразить, что она равна длине окружности), поэтому для данного контура
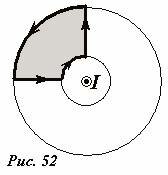
Таким образом, циркуляция по выбранному контуру оказалась равной произведению силы тока на магнитную постоянную, причем не зависимо от радиуса выбранной окружности. Такой красивый результат не может быть случайным – доказано [2], что такое же значение циркуляции получится для любого контура, охватывающего проводник с током, причем не обязательно прямой. А что будет в том случае, если контур не охватывает проводник с током? В этом случае циркуляция будет равна нулю. Очень просто это доказать, для контура, показанного на рис. 52 (проделайте это самостоятельно).
Так как для вектора магнитной индукции справедлив принцип суперпозиции, а циркуляция линейно выражается линейно через индукцию поля, по принцип суперпозиции также справедлив и для циркуляции магнитного поля.
Обобщая все эти положения, дадим окончательную формулировку теоремы о циркуляции: циркуляция вектора магнитной индукции по любому контуру равна сумме токов, пересекающих контур, умноженной на магнитную постоянную
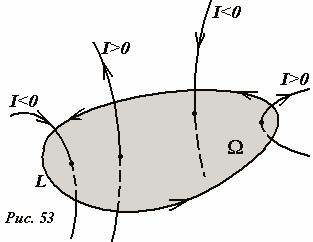
Сумма токов, пересекающих контур \(~I = \sum_k I_k\) , понимается в алгебраическом смысле, то есть токи могут быть положительными, так и отрицательными. Сила тока считается положительной, если его направление и направление обхода образуют правый винт (Рис. 53). Так же как и поток, циркуляция является интегральной (не точечной) характеристикой магнитного поля – из того, что циркуляция по какому-то контуру равна нулю, не следует, что магнитное поле отсутствует – может контур не охватывает ни один ток, или их сумма равна нулю. Токи, не пересекающие контур, так же создают магнитное поле, но циркуляция этого поля по такому контуру равна нулю.
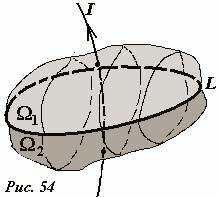
Наконец, уточним, что значит «ток пересекает контур», особенно, если контур не является плоским. Контур это замкнутая линия, поэтому приведенное выражение следует понимать, как ток пересекает любую поверхность (Рис. 54), опирающуюся на контур (или еще говорят «поверхность, натянутую на контур»). Легко доказать, что эта сумма токов, не зависит от выбора поверхности, натянутой на данный контур: из закона сохранения электрического заряда следует, что в статическом случае (когда все токи и все заряды не изменяются с течением времени) сумма токов, пересекающих любую замкнутую поверхность, равна нулю («сколько втекает, столько же вытекает»).