Слободянюк А.И. Физика 10/12.4
§12. Постоянное магнитное поле
12.4 Сила Ампера.
Основное свойство магнитного поля – воздействие на движущиеся электрически заряженные частицы, использовано нами для определения векторной характеристики поля – вектора магнитной индукции. В основу определения этой физической величины мы положили механический момент, действующий на малый контур с током. Но поле действует с некоторой силой на каждую движущуюся заряженную частицу, на каждый участок проводника с током. Сейчас мы получим выражение для силы, действующей на небольшой участок проводника с током, которая называется силой А.М. Ампера.
Выделим на участке цепи, по которой протекает электрический ток силой I, малый прямолинейный участок длиной Δl. Далее нам будет удобно характеризовать этот участок вектором элемента тока \(~I \Delta \vec l\) , направленным вдоль выделенного участка цепи.
Ранее мы подчеркивали, что создать такой уединенный элемент тока невозможно, так постоянный ток может существовать только в замкнутой цепи. Поэтому проверить правильность выражения, для силы, действующей на элемент тока, можно только по тем следствия, которые следуют из формулы для силы. Фактически мы так и поступим – запишем формулу для силы, а затем на ее основании получим выражения, для момента силы, действующей на контур с током.
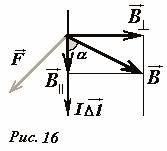
Опыты А.М. Ампера и его последователей свидетельствуют, что сила, действующая на проводник с током, во-первых, пропорциональна силе тока и длине проводника (что очевидно), во-вторых, перпендикулярна проводнику [1]. Разумно предположить, что эта сила пропорциональная индукции магнитного поля. Наконец, опыт показывает, что на ток, текущий параллельно силовым линиям магнитного поля, никакая сила не действует. Следовательно, величина силы должна быть пропорциональна компоненте поля, перпендикулярной направлению тока (Рис. 16). Таким образом, мы приходим к формуле для вычисления модуля силы Ампера
где \(B_{\perp} = B \sin \alpha\) - компонента вектора индукции поля, перпендикулярная направлению тока, α - угол между вектором индукции и направлением тока.
Обратим внимание, что вектор силы Ампера перпендикулярен векторам индукции поля и элемента тока, поэтому в векторной форме выражение для рассматриваемой силы можно представить в виде векторного произведения
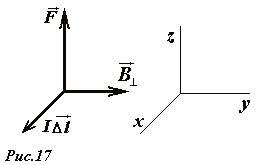
Для правильного определения направления силы Ампера полезно запомнить, что векторы \(~I \Delta \vec l\) , \(~\vec B_{\perp}\) и \(~\vec F_A\) (именно в таком порядке) ориентированы также как оси декартовой системы координат Ox, Oy, Oz в традиционном изображении (Рис.17). Кстати, такая ориентация традиционно называется правой тройкой (а система координат – правой) – поворот от первого вектора ко второму, со стороны третьего происходит против часовой стрелки.
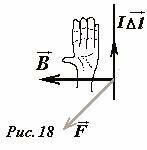
Для тех, кто не в состоянии разобраться в операции векторного произведения, придумано правило левой руки [2] (Рис. 18):
Для определения направления силы Ампера, необходимо расположить кисть левой руки так, чтобы силовые линии магнитного поля входили в ладонь, четыре пальца были направлены вдоль направления тока, тогда отставленный на 90° большой палец укажет направление силы Ампера.
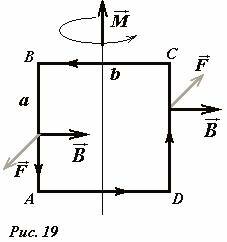
Рассмотрим теперь силы, действующие на прямоугольный контур с током ABCD, длины сторон которого обозначим a и b. Для простоты, будем считать, что вектор индукции \(~\vec B\) однородного магнитного поля лежит в плоскости контура и перпендикулярен одной из сторон контура (Рис. 19). На стороны контура BC и DA сила Ампера не действует, силы, действующие на стороны AB и CD, направлены перпендикулярно плоскости контура в противоположные стороны, их модули равны \(F = IBa\) . Эти силы образуют пару, момент которой не зависит от выбора оси вращения. Поэтому в качестве произвольной оси выберем прямую, параллельную сторонам AB и CD и проходящую через центр контура. Вектор момента силы ориентирован вдоль этой оси и по модулю равен
где \(S = ab\) - площадь контура. Полученное выражение для вектора момента силы, действующего со стороны магнитного поля совпадает с выражением, использованном нами для определения вектора индукции поля, что доказывает справедливость формулы (12) для силы Ампера.
Задание для самостоятельной работы.
- Докажите, что для произвольного контура и его произвольной ориентации выражение (2) для силы Ампера приводит к правильному выражению для момента силы, действующему на контур. Воспользуйтесь подсказкой, что произвольный контур можно представить в виде наложения прямоугольных контуров (Рис. 20).
В заключение данного раздела укажем, что способ получения формулы для силы Ампера нельзя считать математически выводом. Фактически это угадывание формулы, приводящей к правильному выражению для момента силы, действующей на контур, которая верна «по определению» - по определению вектора магнитной индукции. Конечно, здесь используются и экспериментально проверенные факты: пропорциональность силы Ампера Силе тока и ее перпендикулярность направлению тока – все остальное является следствием определения вектора индукции. Кроме того, при разложении вектора индукции на две составляющие мы неявно использовали принцип суперпозиции для индукции магнитного поля, о котором подробнее будет сказано ниже.
Примечания
- ↑ Этот факт был воспринят его открывателями как чрезвычайно странный и удивительный. К началу XIX века физики привыкли к центральным силам, направленным вдоль линии, соединяющей малые тела, подобно гравитационным и электростатическим силам.
- ↑ Для того, чтобы определить, какая рука левая полезно следующее правило: расположите две руки на краю стола ладонями вниз и запомните, что на левой руке большой палец справа!