Слободянюк А.И. Физика 10/12.7
§12. Постоянное магнитное поле
12.7 Расчет индукции магнитного поля.
Закон Био-Саварра-Лапласа и принцип суперпозиции позволяют рассчитать индукцию магнитного поля \(~\vec B\) , создаваемого произвольной системой электрических токов, в произвольной точке пространства. Для этого необходимо разбить все токи на бесконечно малые участки \(~(I \Delta \vec l)_k\) , записать выражения для векторов для индукции поля \(~(\Delta \vec B)_k\) , создаваемых этими элементами (пользуясь законом Био-Саварра-Лапласа) и просуммировать полученные выражения (что позволяет принцип суперпозиции) для всех участков тока
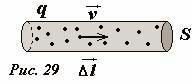
Рассмотрим еще раз участок проводника с током (Рис. 29) . Выражение для элемента тока \(~I \Delta \vec l\) записывается также в виде \(~I \Delta \vec l = \vec j S \Delta l = \vec j \Delta V\) . В том случае, когда электрические токи не являются линейными, а пространственно распределенными (то есть текут не только по тонким проводам), выражение для элемента тока \(~I \Delta \vec l\) следует заменить эквивалентным \(~\vec j \Delta V\) и провести суммирование по всем элементам объема., где протекают электрические токи.
Конечно, такое суммирование часто представляет собой громоздкую математическую задачу (в конце концов, для его выполнения можно воспользоваться компьютером), но, с физической точки зрения, изложенный метод дает полное решение задачи.
Рассмотрим несколько примеров расчета индукции магнитного поля по изложенной выше методике.
12.7.1 Магнитное поле кругового тока.
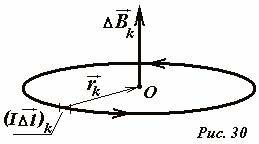
Пусть постоянный электрический ток силой I протекает по плоскому круглому контуру радиуса R. Найдем индукцию поля в центре кольца в точке O (Рис. 30). Мысленно разобьем кольцо на малые участки, которые можно считать прямолинейными, и применим закон Био-Саварра-Лапласа для определения индукции поля, создаваемого этим элементом, в центре кольца. В данном случае вектор элемента тока \(~(I \Delta \vec l)_k\) и вектор \(~\vec r_k\) , соединяющий данный элемент с точкой наблюдения (центр кольца), перпендикулярны, поэтому \(\sin \alpha = 1\) . Вектор индукции поля, созданного выделенным участком кольца, направлен вдоль оси кольца, а его модуль равен
Для любого другого элемента кольца ситуация абсолютно аналогична – вектор индукции также направлен по оси кольца, а его модуль определяется формулой (1). Поэтому суммирование этих векторов выполняется элементарно и сводится к суммированию длин участков кольца
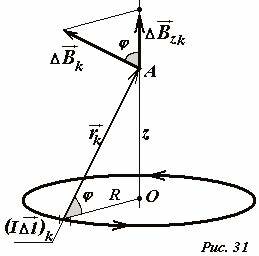
Усложним задачу - найдем индукцию поля в точке A, находящейся на оси кольца на расстоянии z от его центра (Рис. 31). По-прежнему, выделяем малый участок кольца \(~(I \Delta \vec l)_k\) и строим вектор индукции поля \(~(\Delta \vec B)_k\) , созданным этим элементом, в рассматриваемой точке. Этот вектор перпендикулярен вектору \(~\vec r\) , соединяющему выделенный участок с точкой наблюдения. Векторы \(~(I \Delta \vec l)_k\) и \(~\vec r_k\) , как и ранее, перпендикулярны, поэтому \(\sin \alpha = 1\) . Так кольцо обладает осевой симметрией, то суммарный вектор индукции поля в точке A должен быть направлен по оси кольца. К этому же выводу о направлении суммарного вектора индукции можно прийти, если заметить, что каждому выделенному участку кольца имеется симметричный ему с противоположной стороны, а сумма двух симметричных векторов направлена вдоль оси кольца. Таким образом, для того чтобы определить модуль суммарного вектора индукции, необходимо просуммировать проекции векторов на ось кольца. Эта операция не представляет особой сложности, если учесть, расстояния от всех точек кольца до точки наблюдения одинаковы \(~r = r_k = \sqrt{R^2 + z^2}\) , а также одинаковы углы φ между векторами \(~(\Delta \vec B)_k\) и осью кольца. Запишем выражение для модуля искомого суммарного вектора индукции
Из рисунка следует, что \(~\cos \varphi = \frac{R}{r}\) , с учетом выражения для расстояния r, получим окончательное выражение для вектора индукции поля
Как и следовало ожидать, в центре кольца (при z = 0) формула (3) переходит в полученную ранее формулу (2).
Задания для самостоятельной работы.
- Постройте график зависимости индукции поля (3) от расстояния до центра кольца.
- Сравните полученную зависимость (3) с выражением для модуля напряженности электрического поля, создаваемого равномерно заряженным кольцом (§9.6). Объясните возникшие принципиальные различия между этими зависимостями.
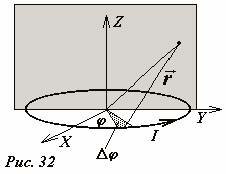
Используя общий рассматриваемый здесь метод, можно рассчитать индукцию поля в произвольной точке. Рассматриваемая система обладает осевой симметрией, поэтому достаточно найти распределение поля в плоскости, перпендикулярной плоскости кольца и проходящей через его центр. Пусть кольцо лежит в плоскости xOy (рис.32), а поле рассчитывается в плоскости yOz. Кольцо следует разбить на малые участки, видимые из центра под углом Δφ и просуммировать поля создаваемые этими участками. Можно показать (попробуйте проделать это самостоятельно), что компоненты вектора магнитной индукции поля, создаваемого одним выделенным элементом тока, в точке с координатами (y,z) рассчитываются по формулам:
Необходимое суммирование не может быть проведено аналитически, так как при переходе от одного участка кольца к другому изменяются расстояния до точки суммирования. Поэтому «простейший» способ провести такое суммирование – использовать компьютер.
Если же известно значение вектора индукции (или хотя бы имеется алгоритм его расчета) в каждой точке, то можно построить картину силовых линий магнитного поля. Очевидно, что алгоритм построения силовых линий векторного поля не зависит от его физического содержания, а такой алгоритм был кратко рассмотрен нами при изучении электростатики.
На рис. 33 картина силовых линий рассчитана при разбиении кольца на 20 частей, этого оказалось вполне достаточно, так как и при 10 интервалах разбиения получался практически тот же рисунок.
Рассмотрим выражение для индукции поля на оси кольца на расстояниях значительно больших радиуса кольца z >> R. В этом случае формула (3) упрощается и приобретает вид
где \(I \pi R^2 = IS = p_m\) - произведение силы тока на площадь контура, то есть магнитный момент кольца. Эта формула совпадает (если как обычно, заменить μ0 в числителе на ε0 в знаменателе) с выражением для напряженности электрического поля диполя на его оси.
Такое совпадение не случайно, более того, можно показать, что подобное соответствие справедливо для любой точки поля, находящейся на больших расстояниях от кольца. Фактически малый контур с током является магнитным диполем (два одинаковых малых противоположно направленных элемента тока) – поэтому его поле совпадает с полем электрического диполя. Чтобы ярче подчеркнуть этот факт, на рис. 34 приведена картина силовых линий магнитного поля кольца, на больших расстояниях от него (сравните с аналогичной картиной для поля электрического диполя).
12.7.2 Магнитное поле прямого тока.
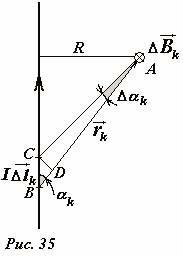
Рассчитаем индукцию магнитного поля, создаваемого бесконечным [1] проводником, по которому протекает электрический ток силой I (Рис. 35) Методика расчет остается прежней: мысленно разбиваем проводник на малые участки \(~I \Delta \vec l_k\). Согласно закона Био-Саварра-Лапласа в произвольной точке A, находящейся на расстоянии R от проводника, произвольный элемент тока создает магнитное поле, вектор индукции которого \(~(\Delta \vec B)_k\) направлен перпендикулярно плоскости, содержащей проводник и рассматриваемую точку (на Рис. 35 - перпендикулярно плоскости рисунка), модуль этого вектора равен
где rk - расстояние от выбранного участка проводника до точки наблюдения, αk - угол между проводником и направлением от элемента тока до точки наблюдения.
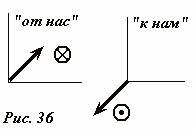
Договоримся об еще одном общепринятом соглашении. Достаточно часто приходится изображать векторы, перпендикулярные плоскости рисунка. В этом случае эти векторы изображаются в виде (рис. 36): небольшого кружка с точкой в центре, если вектор направлен «на нас» (видно «острие» вектора); кружка с перекрестием, если вектор направлен от нас (видно «оперение» вектора).
Векторы поле, созданных всеми другими участками проводника, направлены также, поэтому суммирование векторов в данном случае сводится к суммированию их модулей. Но даже вычислить сумму модулей не просто, так как для различных участков проводника расстояния rk и αk различны. Тем не менее, такое суммирование выполнимо, его результат выражается формулой, определяющей величину индукции магнитного поля бесконечного прямого тока
здесь не приведено вычисление последней суммы (которая равна \(~\sum_k \frac{\Delta l_k}{r^2_k} \sin \alpha_k = \frac{2}{R}\)), поверьте пока в справедливость полученного выражения, хотя бы потому, что оно имеет богатый физический смысл. Во-первых, эта формула совпадает с выражением для напряженности электрического поля, создаваемого бесконечной прямой равномерно заряженной нитью; во-вторых, оно соответствует результату опытов А.М. Ампера по изучению взаимодействия параллельных токов. Действительно, если один проводник создает магнитное поле, индукция которого обратно пропорциональна расстоянию до проводника, то на второй проводник действует сила Ампера, пропорциональная индукции поля, то есть обратно пропорциональная расстоянию между проводниками.
Дадим теперь строгий вывод формулы для суммы, фигурирующей в выражении (2). Проще всего она выводится с помощью операции интегрирования, но здесь мы дадим ее геометрический вывод. Для начала с помощью рис. 35 преобразуем каждое слагаемое этой формулы \(~\frac{\Delta l_k}{r^2_k} \sin \alpha_k\) . Заметим, что произведение \(~\Delta l_k \sin \alpha_k\) равно длине отрезка CD, перпендикулярного вектору \(~\vec r_k\) - \(~\Delta l_k \sin \alpha_k = |CD|\) . Отношение же длины этого отрезка к расстоянию rk для малых длин элементов тока равно малому углу Δαk, под которым виден выделенный участок проводника
( точнее, это отношение равно тангенсу угла, который для малых углов равен самому углу, измеренному в радианах). Из того же рисунка следует, что отношение \(~\frac{r_k}{\sin \alpha_k} = R\) равно расстоянию от точки наблюдения до проводника и не зависит от выбора участка проводника. С учетом этого соотношения и формулы (2) получим
Таким образом, вычисление суммы (2) сводится к вычислению суммы \(~\sum_k \Delta \alpha_k \sin \alpha_k\) , в которой все углы являются малыми (поэтому число слагаемых велико), пусть углы αk изменяются от нуля до некоторого предельного значения αmax.
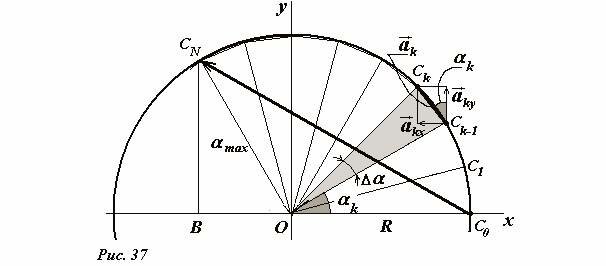
Для вычисления этой суммы применим искусственный прием (он встретится нам и в дальнейшем). Возьмем окружность (Рис. 37) радиуса R и разобьем ее точками C0, C1, C2, …, CN на малые участки, угловой размер каждого равен Δα.
Хорды, которые образованы точками разбиения будем рассматривать как векторы \(~\vec a_0 = \overrightarrow {C_0 C_1}, \vec a_1 = \overrightarrow {C_1 C_2}, \ldots, \vec a_k = \overrightarrow {C_k C_{k+1}}, \ldots\) . Сумма этих векторов очевидна – это вектор \(~\vec A\) , соединяющий начальную и конечную точки разбиения окружности:
Теперь, внимание, если справедливо векторное равенство, то справедливо аналогичное выражение для любой проекции этих векторов. Введем декартовую систему координат с началом в центре окружности, ось Ox которой проходит через начальную точку. Длины построенных вписанных векторов равны \(~|\vec a_k| = R \Delta \alpha_k\) (точнее, это длина дуги, но для малых углов, длина стягивающей хорды стремится к длине дуги). Из рисунка 37 следует, что проекции этого вектора на оси координат равны, соответственно,
Проецируя равенство (4) на оси координат получим
Проекции суммарного вектора \(~\vec A\) на оси координат находятся просто
Сравнивая выражения (5) и (6) получим искомые формулы
Еще раз подчеркнем, что суммирование в этих формулах проводится в пределах изменения угла от нуля до предельного значения αmax.
Осталось принять во внимание, что бесконечный прямой проводник виден из любой точки вне его под углом αmax = π, поэтому искомая сумма выражается формулой
что и требовалось доказать.
Оценим длину «бесконечного» в данном случае проводника – во сколько раз длина проводника должна быть больше расстояния до точки наблюдения, что бы погрешность расчета индукции поля по формуле (2), примененной к проводнику конечной длины, была пренебрежимо малой.
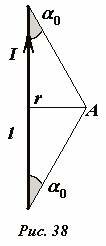
Пусть длина прямого проводника равна l, а индукция поля рассчитывается в точке A, находящейся на расстоянии r (считаем, что r << l) от центра проводника (Рис. 38). С помощью полученных формул можно получить точное выражение для индукции поля в рассматриваемой точке \(~\bar{B} = \frac{\mu_0 I}{2 \pi r} \cos \alpha_0\) , где α0 - угол между проводником и направлением на точку наблюдения с конца проводника.
Если считать проводник бесконечно длинным, то индуктивность поля должна рассчитываться по формуле (которую в данном случае следует считать приближенной) \(~\tilde{B} = \frac{\mu_0 I}{2 \pi r}\) . Относительная погрешность этой формулы равна [2]
Такая ошибка будет допущена, если отношение длины проводника к расстоянию до точки наблюдения равно \(~\frac{l}{r} = \frac{2}{\varepsilon}\). Так для относительной ошибки ε = 1% искомое отношение равно \(~\frac{l}{r} \approx 15\). Итак, в рассмотренном случае «бесконечность» равна 15.