Слободянюк А.И. Физика 10/13.2
§13. Взаимодействие магнитного поля с веществом
13.2 Описание магнитного поля в веществе. Магнитные характеристики вещества.
В общем случае описание влияния вещества на магнитное поле является очень сложной математическое задачей. Магнитное поле приводит к намагничиванию вещества, то есть вектор намагниченности вещества зависит от индукции магнитного поля, действующего на вещество \(~\vec J = G(\vec B)\). Чрезвычайная сложность этой связи обусловлена целым рядом причин:
- В данном выражении намагниченность выделенного объема вещества зависит не только от магнитной индукции не только внешнего поля \(~\vec B_0\), которое может быть известно, но и поля \(~\vec B'\) , возникающего благодаря намагничиванию других частей вещества, которое само подлежит определению.
- Связь между намагниченностью и индукцией поля часто бывает нелинейной, что связано с эффектами насыщения, о которых мы поговорим чуть позже.
- Многие вещества обладают магнитной анизотропией[1], то есть величина намагниченности может зависеть от направления, поэтому векторы намагниченности и индукции поля в общем случае не параллельны.
- Рассматриваемая связь может быть не функциональной, так в ферромагнетиках намагниченность определяется полем не только в данный момент времени, но и «предысторией», то есть вещество частично «запоминает» какое поле действовало раньше. Подобный эффект называется магнитным гистерезисом.
Для расчета поля в присутствии магнетиков, необходимо уметь рассчитывать индукцию поля при заданном распределении намагниченности вещества, то есть \(~\vec B' = F(\vec J)\). Во многих случаях эта задача может быть решена (что тоже не просто) с помощью закона Био-Савара и принципа суперпозиции.
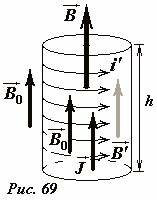
Конечно, мы не имеем возможности изучить все методы решения рассматриваемой задачи о взаимодействии магнитного поля веществом, а ограничим наше рассмотрением простейшего случая. Пусть длинный прямой круговой цилиндр, изготовленный из однородного изотропного магнетика находится во внешнем однородном магнитном поле, постоянный вектор индукции \(~\vec B_0\) которого направлен вдоль оси цилиндра (Рис. 69).
Под действием магнитного поля вещество цилиндра намагничивается однородно, то есть вектор намагниченности \(~\vec J\) оказывается постоянным как по величине, так и по направлению. Действительно, если вещество и поле однородны, то почему намагниченность должна изменяться?
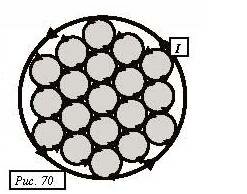
Представим атомы вещества цилиндра в виде одинаковых контуров, магнитные моменты которых ориентированы вдоль оси цилиндра. Стилизованный вид этих контуров в сечении, перпендикулярном оси цилиндра показан на Рис. 70. Такая упорядоченная структура молекулярных токов приводит к возникновению индуцированного тока, текущего по поверхности цилиндра (все токи внутри объема компенсируют друг друга). Такие токи, возникающие на поверхности намагниченного образца называются токами намагничивания.
Обозначим высоту выделенной части цилиндра h. Тогда суммарная сила тока, текущего по поверхности этой части цилиндра может быть представлена в виде \(I' = i'h\) , где i′ - линейная плотность поверхностного тока. Следовательно, магнитный момент рассматриваемой части цилиндра равен произведению силы поверхностного тока на площадь поперечного сечения цилиндра \(P_m = I'S = i'hS\). С другой стороны по определению он равен произведению намагниченности вещества на объем выделенной части \(P_m = JV = JhS\). Из сравнения этих двух выражений получаем важное соотношение: поверхностная плотность тока намагничивания равна модулю вектора намагниченности вещества
Можно показать, что , когда вектор намагниченности не параллелен поверхности образца, плотность поверхностного тока равна тангенциальной составляющей вектора намагниченности
В случае неоднородной намагниченности возможно возникновение токов намагниченности и внутри объема магнетика.
Сравним данные рассуждения с описанием электрического поля в диэлектриках. Там под действием электрического поля каждая молекула приобретает электрический дипольный момент, суммарное действие которых приводит к возникновению поверхностных индуцированных (поляризационных) зарядов. Поверхностная плотность этих зарядов равна нормальной составляющей вектора поляризации. При неоднородной поляризации возможно возникновение поляризационных зарядов внутри объема диэлектрика.
Обратимся еще раз к рисунку 69. Магнитное поле внутри цилиндра теперь можно представить как суперпозицию внешнего поля индукции \(~\vec B_0\) и поля, созданного током намагниченности \(~\vec B'\). Последнее может быть выражено через вектор намагниченности. Воспользуемся формулой для индукции магнитного поля внутри длинного соленоида
в которой произведение плотности намотки n на силу тока I, фактически является силой тока, пересекающего единицу длины соленоида, то есть совпадает с поверхностной плотностью тока \(i = nI\). Следовательно, и в случае намагниченного цилиндра индукция поля[2], созданного поверхностным током намагниченности, равна
Итак, индукция суммарного поля внутри цилиндра равна
Теперь, казалось бы, следует выразить вектор намагниченности через индукцию поля внутри цилиндра \(~\vec J = G(\vec B)\) и получить уравнения для определения искомой индукции поля. Однако так уже исторически сложилось, что намагниченность вещества традиционно связывается с иной характеристикой[3] магнитного поля в веществе. Поэтому в данном простейшем случае (когда все рассматриваемые векторы параллельны друг другу и поверхности рассматриваемого тела) вектор намагниченности выражается через индукцию внешнего (только внешнего, а не полного) поля, которую принято записывать в виде
где коэффициент пропорциональности χ - является безразмерной характеристикой вещества и называется его магнитной восприимчивостью. Подставляя выражение (6) для намагниченности в формулу (5), получаем
где коэффициент \(\mu = 1 + \chi\) называется магнитной проницаемостью вещества. Эта величина показывает, во сколько раз вещество изменяет индукцию магнитного поля. Подчеркнем, что такая простая связь (7) между полем в веществе и полем вакууме (разумеется, при одинаковых источниках внешнего поля) выполняется только в простейших частных случаях. Для ее применимости необходимо выполнение следующих условий:
- Вещество должно быть однородным.
- Везде на границах тел вектор индукции поля должен быть параллелен границе раздела.
Заметим, что для многих веществ магнитная восприимчивость зависит от индукции магнитного поля. В этом случае следует определить проницаемость немного иным способом. Магнитная восприимчивость определяется как отношение изменения намагниченности к изменению индукции поля (умноженной на магнитную постоянную, впрочем этот множитель обязан выбранной системе единиц)
Если считать изменение индукции внешнего поля малой (точнее бесконечно малой) величиной, то магнитная восприимчивость, определяемая по формуле (8), является функцией индукции поля χ(B0). Если же намагниченность пропорциональна индукции внешнего поля, то восприимчивость вещества постоянна и в таком случае формула (8) приводит к зависимости (6).
Замените J на x, B0 на t и вспомните все математические рассуждения о средней и мгновенной скорости, о равномерном и неравномерном движении – их можно повторить и здесь.
Примечания
- ↑ Напомним, анизотропия – зависимость свойств вещества от направления в пространстве.
- ↑ Так и хочется сказать «индукция индуцированного поля», но это уже слишком...
- ↑ Эта характеристика называется напряженностью магнитного поля. Она не имеет явного физического смысла, а является вспомогательной величиной, помогающей рассчитывать поле в магнетиках. Заметим, что при описании электростатического поля в диэлектриках вводится вспомогательная величина – индукция электрического поля. Видите, все сделано для того, чтобы окончательно запутать несчастных учащихся! Ни индукцию электрического поля, ни напряженность магнитного поля в дальнейшем мы использовать не будем.