Слободянюк А.И. Физика 10/18.7

Содержание книги

Предыдующая страница

§18. Переменный электрический ток

18.7 Резонанс токов.

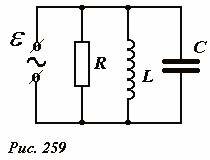
Рассмотрим теперь цепь, состоящую из тех же элементов, только соединенных параллельно (Рис. 259). Расчет токов в данной цепи не вызывает особых сложностей, так как напряжения на всех элементах этой цепи одинаковы и равны ЭДС источника (если, по-прежнему, пренебречь его внутренним сопротивлением). Поэтому, для сил токов во всех ветвях справедливы выражения, полученные нами ранее в разделах 18.3-18.5. Следовательно, для определения силы суммарного тока I(t), протекающего через источник, достаточно просуммировать токи, протекающие через резистор, конденсатор и катушку индуктивности:

\(~I(t) = I_R(t) + I_C(t) + I_L(t)\) . (1)

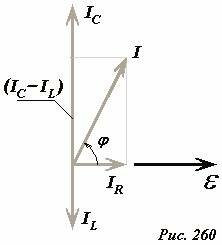
Для определения амплитудного значения силы суммарного тока, построим векторную диаграмму этих токов (Рис. 260). В данном случае ее построения следует начинать с вектора, изображающего колебания напряжения на элементах цепи

\(~\varepsilon = U_0 \cos \omega t\) . (2)

Теперь относительно этого вектора следует построить векторы, изображающие силы токов. С помощью построенной диаграммы выражаем амплитуду силы результирующего тока

\(~I^2_0 = I^2_{R0} + (I_{C0} - I_{L0})^2\) . (3)

Наконец, выражаем амплитуды сил токов через напряжение, создаваемое источником \(I_{R0} = \frac{U_0}{R}\), \(I_{C0} = \omega C U_0\) , \(I_{L0} = \frac{U_0}{\omega L}\), подставим их в формулу (3) и выразим искомое значение амплитудного значения силы тока

\(~I_0 = U_0 \sqrt{\frac{1}{R^2} + \left(\omega C - \frac{1}{\omega L} \right)^2}\) . (4)

Также с помощью построенной векторной диаграммы найдем сдвиг фаз между током и напряжением источника

\(~\operatorname{tg} = \frac{I_{C0} - I_{L0}}{I_{R0}} = \frac{\omega C - \frac{1}{\omega L}}{\frac{1}{R}} = R \left(\omega C - \frac{1}{\omega L} \right)\) . (5)

Итак, мы получили формулы, определяющие зависимость силы тока в цепи от времени \(I = I_0 \cos (\omega t + \varphi)\).

Проанализируем зависимость амплитуды силы тока (4) от частоты источника. В данном случае эта функция имеет минимум, который достигается, когда второе слагаемое под корнем обращается в нуль

\(~\omega C - \frac{1}{\omega L} = 0\) ,

то есть при частоте равной

\(~\omega_0 = \frac{1}{\sqrt{LC}}\) . (6)

В этом случае амплитуда силы тока равна

\(~I_0 = \frac{U_0}{R}\) (7)

и не зависит от значений емкости и индуктивности цепи. Физическая причина подобного поведения тока в цепи, аналогична рассмотренной в предыдущем разделе при изучении резонанса напряжений. В этом случае в противофазе находятся токи, протекающие через конденсатор и через катушку индуктивности, поэтому ток циркулирует в контуре L − C и «не выходит» во внешнюю цепь. И в этом случае происходит постоянное перетекание энергии электрического поля конденсатора в энергию магнитного поля катушки индуктивности.

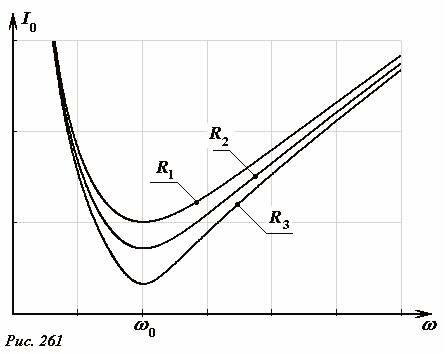
На рис. 261 показаны графики зависимостей амплитудного значения силы тока от частоты источника при различных значениях активного сопротивления резистора, причем R₁ < R₂ < R₃. Рассмотренное в данном разделе явление резкого уменьшения силы суммарного тока в цепи с параллельно соединенными конденсатором и катушкой индуктивности называется резонансом токов, а соответствующая частота (6), при которой оно наблюдается называется резонансной частотой.

Отметим, что при резонансе токов уменьшается именно суммарный ток, в то время как токи через конденсатор и катушку индуктивности могут достигать больших значений.

Примечания

Следующая страница