Слободянюк А.И. Физика 10/19.1.I

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.1.1 Гармоническая волна на струне.

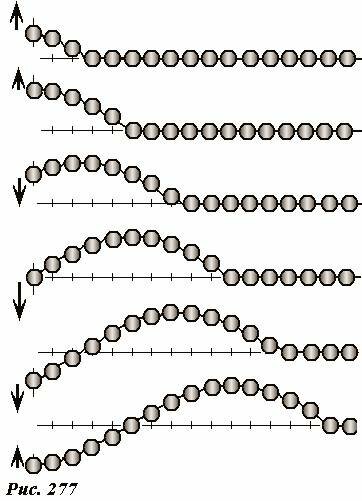
Волна это колебание, распространяющееся в пространстве. Поэтому функция, описывающая волну должна зависеть как от времени, так и от пространственных координат. Для получения такой функции, рассмотрим простейший пример возникновения и распространения волны вдоль длинной цепочки шариков, связанных упругими нитями (Рис. 277). Пусть крайний шарик начинает совершать гармонические колебания. При его смещении от положения равновесия с некоторым запаздыванием начнет двигаться его ближайший сосед, который потянет за собой следующий и так далее. Причем движение каждого следующего шарика будет запаздывать по сравнению с предыдущим. Через четверть периода после начала колебания первого шарика он изменит направление движения на противоположное, в это же время некоторые из шариков будут продолжать движение в прежнем направлении. Они изменят направление движение чуть позже. Таки образом по цепочке будет распространяться волна. По прошествии некоторого промежутка времени все шарики придут в движение.

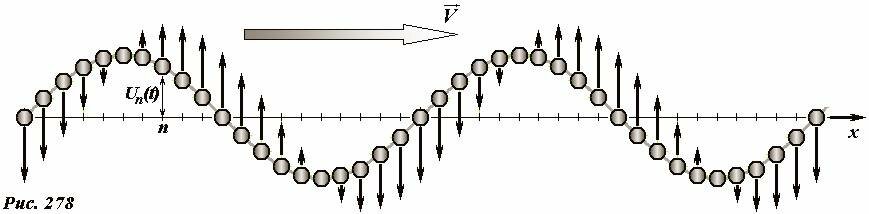
Если первый шарик совершает гармонические колебания под действием внешней силы, то сила натяжения нити служит периодической вынуждающей силой для второго шарика, поэтому второй шарик в установившемся режиме также будет совершать гармонические колебания с той же частотой, что и первый. Продолжая эти рассуждения, можем прийти к выводу, что в установившемся режиме все шарики будут совершать гармонические колебания с одной и той же частотой, равной частоте вынуждающей силы, действующей на первый шарик. Мы не будем подробно описывать переходной режим установления колебаний, а сразу рассмотрим более простой режим установившихся колебаний, когда все шарики колеблются с одинаковыми частотами и амплитудами (Рис. 278).

Пронумеруем все шарики целочисленным индексом n (n = 0,1,2...). В качестве координаты каждого шарика выберем его отклонение от его собственного положения равновесия U_n(t). На приведенном рисунке для наглядности все отклонения происходят в направлении, перпендикулярном цепочке в положении равновесия. Согласно проведенным рассуждениям эти отклонения изменяются по гармоническим законам с постоянными частотами и амплитудами, поэтому описываются функциями

\(~U_n(t) = A \cos (\omega t + \varphi)\) , (1)

где φ_n - фаза колебаний n-го шарика. Так как амплитуды и частоты колебаний всех шариков равны, то единственное, чем они могут отличаться, так это фазы.

Так как все шарики в рассматриваемой цепочки равноправны, то разности фаз колебаний двух соседних шариков должны быть равны. Обозначим эту разность фаз − Δφ. Она действительно должна быть отрицательной – ведь колебания каждого следующего запаздывают по отношению к предыдущему. С учетом этого замечания функцию (1) можно представить в виде

\(~U_n(t) = A \cos (\omega t - n \Delta \varphi)\) . (2)

Фаза колебаний крайнего шарика принята равной нулю – как обычно выбор начальной фазы произволен, существенную роль играют только разности фаз.

Фактически набор функций (2) можно рассматривать как функцию двух аргументов: времени t и номера шарика, который определяется его пространственным положением. Номер шарика можно выразить через его координату

\(~n = \frac{x_n}{l}\) , (3)

здесь мы ввели ось Ox, направленную вдоль цепочки, тогда x_n - координата n-го шарика, l - расстояние между центрами шариков. Наконец, «забудем», что наша цепочка состоит из дискретных шариков, то есть будем считать, что шарики малы настолько, что мы воспринимаем цепочку как сплошную нить. Тогда координату шарика следует рассматривать как координату некоторой точки нити и считать эту координату непрерывной. В этом пределе выражение (2) можно заменить функцией двух непрерывных переменных

\(~U(x,t) = A \cos (\omega t - kx)\) . (4)

Здесь мы обозначили \(~k = \frac{\Delta \varphi}{l}\), причем при переходе к непрерывной нити числитель и знаменатель этой дроби теряют свой смысл (каждое из них стремится к нулю). Однако их отношение может оказать конечным, смысл этого параметра мы выясним чуть ниже.

Итак, мы получили функцию (4), которая описывает волну, распространяющуюся вдоль упругой нити.

Волна, описываемая функцией (4), называется гармонической волной. Если зависимость возмущения среды от времени описывается гармонической функцией (напоминаем, синус или косинус) с одной частотой, то волна называется монохроматической. Отметим, что пространственная структура монохроматической волны может иметь вид, отличный от гармонической, описываемой функцией (4).

В природе существуют волны, которые описываются иными функциями, отличными от полученной нами. Однако, гармонические волны являются наиболее простыми с точки зрения их математического описания (в том же смысле наиболее простыми являются и гармонические колебания). Кроме того, любая волна может быть представлена в виде суммы (суперпозиции) гармонических волн с применением разложения Фурье, о котором говорили при изучении колебаний. Наконец, как это ни странно, гармонические волны достаточно широко распространены в природе. Поэтому наше изучение волн основывается на функциях, подобных (4).

Уточним смысл полученной функции (4) и входящих в нее параметров. Прежде всего, отметим, что аргумент косинуса \(\varphi = \omega t - kx\) - называется фазой волны.

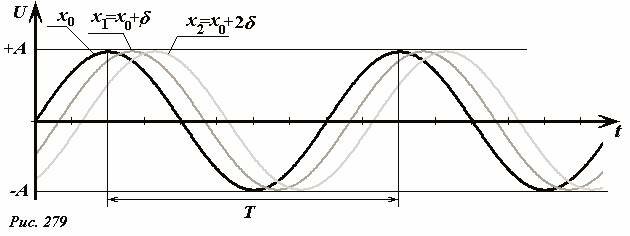
Если зафиксировать координату точки x = x₀ = const, функция (4) станет функцией единственной переменной – времени

\(~U(x_0,t) = A \cos (\omega t - kx_0)\) . (5)

Изучению таких функций мы посвятили достаточно времени – эта функция описывает гармонические колебания. В данном конкретном случае – колебания точки нити, координата которой равна x₀. Иными словами, при подстановке x = x₀ = const мы выбираем единственную точку нити и следим за ней в течение длительного промежутка времени. В функции (5) координата точки x₀ является параметром, при переходе к другой точке \(x_1 = x_0 + \delta\) мы получим функция, которая описывает закон движения этой точки - те же гармонические колебания, только немного отстающие по времени (Рис. 279).

Параметр функции A - равен максимальному отклонению точки от положения равновесия и называется амплитудой волны. Параметр ω, как и ранее, называется круговой частотой волны. Она связана с периодом колебаний. Напомним, при изменении времени на один период колебания T его фаза изменяется на 2π, поэтому ωΔt = ωT = 2π. Из этого соотношения следует связь между круговой частотой и периодом колебаний

\(~\omega = \frac{2 \pi}{T}\) (6)

и его частотой (числом колебаний в единицу времени)

\(~\nu = \frac{1}{T} = \frac{\omega}{2 \pi}\) . (7)

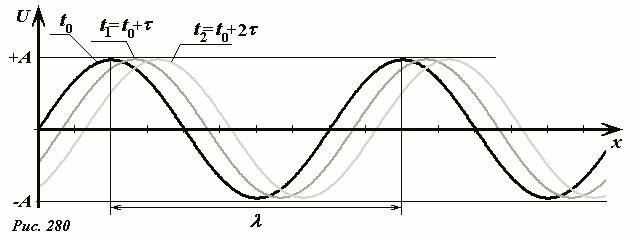
Зафиксируем теперь в функции (4) момент времени t = t₀ = const и получим тем самым функцию одной переменной координаты x:

\(~U(x,t_0) = A \cos (\omega t_0 - kx)\) . (8)

Эта функция описывает отклонения точек нити в фиксированный момент времени, то есть представляет собой мгновенную «фотографию» нити, ее профиль в этот момент времени. Здесь время t = t₀ = const является параметром функции. При переходе к другому моменту \(t_1 = t_0 + \tau\) мы получим профиль волны в этот новый момент времени, очевидно, просто смещенный относительно начального (Рис. 280).

Параметры этой функции также понятны: амплитуда А - максимальное отклонение профиля волны от положения равновесия, ясно, что она совпадает амплитудой, определенной ранее. Расстояние между двумя ближайшими максимумами (или минимумами) называется длиной волны λ. Длина волны является пространственным аналогом временной характеристики – периода колебаний T, ее даже можно назвать пространственным периодом. Так при изменении координаты на расстояние равное длине волны фаза волны изменяется на 2π, поэтому kΔx = kλ = 2π. Следовательно, параметр k, который называется волновым числом, связан с длиной волны соотношением

\(~k = \frac{2 \pi}{\lambda}\) . (9)

Таким образом, волна характеризуется: амплитудой, временными параметрами (период, частота, круговая частота – все они связаны между собой), пространственными параметрами (длиной волны и волновым числом).

Как мы показали, функция двух переменных (4), описывает волну, распространяющуюся в положительном направлении оси Ox, найдем скорость распространения этой волны.

Подчеркнем, что скорость распространения волны в некоторой среде отличается от скорости движения самих частиц среды. Так на рис. 278 построены векторы скоростей движения отдельных шариков, эти скорости могут быть найдены традиционным образом. Так если координата шарика изменяется по закону (2), то его скорость описывается функцией

\(~\upsilon_n = U'_n(t) = -A \omega \sin (\omega t - n \Delta \varphi)\) .

Более того, в рассмотренном примере векторы скоростей частиц и скорости распространения волны \(~\vec V\) взаимно перпендикулярны.

Проще всего, для определения (и измерения) скорости распространения волны выбрать ее некоторый максимум и проследить за его распространением. Так в максимуме фаза волны, описываемая функцией (4) равна \(~\frac{\pi}{2}\) и остается постоянной. Впрочем, можно выбрать любую другую точку (минимум, перегиб) профиля волны (но не точку среды!) и наблюдать за ней. Важно, что эта выбранная точка профиля волны характеризуется постоянной фазой. Поэтому ее координата изменяется со временем так, что величина ωt − kx = const остается постоянной. Следовательно, скорость волны (которую мы обозначим с) определяется формулой

\(~c = \frac{\Delta x}{\Delta t} = \frac{\omega}{k}\) . (10)

К этой же формуле можно прийти и чисто математическим путем, рассматривая функцию (8) и ее графики при различных значениях выбранного момента времени. Для этого рассмотрим функцию, описывающую профиль волны в момент времени \(t_1 = t_0 + \tau\), и преобразуем ее следующим образом

\(~U(x,t_1) = A \cos (\omega t_1 - kx) = A \cos (\omega (t_0 + \tau) - kx) = A \cos (\omega t_0 - (kx - \omega \tau)) = A \cos \left(\omega t_0 - k \left(x - \frac{\omega}{k} \tau \right) \right) = U \left(x - \frac{\omega}{k} \tau, t_0 \right)\) . (11)

Мы получили, что график этой функции совпадает с графиком профиля в момент времени t₀, только сдвинут относительно его на величину \(~\Delta x = \frac{\omega}{k} \tau\), иными словами это расстояние прошла волна за промежуток времени τ, откуда следует, что эта волна распространяется со скоростью, определяемой формулой (10). Рассуждая аналогично можно прийти к выводу, что функция

\(~U(x,t) = A \cos (\omega t + kx)\) (12)

описывает гармоническую волну, распространяющуюся в отрицательном направлении оси Ox.

Проведенные преобразования (11) легко могут быть обобщены на случай произвольной функции, аргументом которой является (x − ct). Действительно, профиль графика произвольной функции F(x − ct) при изменении времени t остается неизменным, и только смещается со скоростью c в положительном направлении оси Ox. Следовательно, функция F(x − ct) может описывать произвольное возмущение среды, распространяющееся в пространстве, то есть волну. Аналогично, функция F(x + ct) описывает волну постоянного профиля, распространяющуюся в отрицательном направлении оси Ox.

Используя соотношения между параметрами волны, выражение для скорости волны (10) может быть представлено в нескольких эквивалентных формах

\(~c = \frac{\omega}{k} = \lambda \nu = \frac{\lambda}{T}\) . (13)

Последнее соотношение наиболее просто для запоминания (и понимания!): за один период колебания волна проходит расстояние, равное длине волны.

Следует подчеркнуть, для реальных волн частота и длина волны не являются независимыми параметрами. Если ее частота задается частотой колебаний источника, то скорость распространения волн зависит от свойств среды. Поэтому длина волны определяется частотой источника и скоростью распространения волн. Заметим, что для многих волн скорость их распространения также может зависеть от частоты. Явление зависимости скорости волны от ее частоты называется дисперсией волн. Кроме того, в некоторых случаях скорость волны зависит и от ее амплитуды.

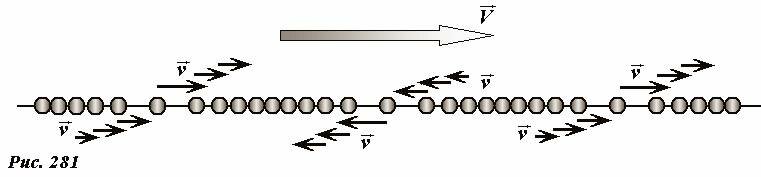
Мы рассмотрели и математически описали поперечную волну, которой направление движения частиц среды перпендикулярно направлению распространения волны. С помощью рассмотренного примера (упругая цепочка шариков) легко представить себе продольную волну, в которой направления движения частиц совпадает с направлением распространения самой волны (Рис.281).

В такой волне все шарики совершают гармонические колебания относительно собственного положения равновесия, причем движение каждого шарика происходит вдоль оси цепочки. Если в положении равновесия шарики расположены на одинаковом расстоянии друг от друга, то координата n-го шарика задается формулой \(x_n = nl\). В качестве переменной величины, описывающей движение каждого шарика может выступать его смещение относительного его собственного положения равновесия U_n(t). В продольной гармонической волне эти функции описываются гармоническими функциями с одинаковыми частотами и амплитудами, но монотонно изменяющимися начальными фазами колебаний. В этом случае волна представляет собой распространяющиеся области «сгустков и разряжений» шариков.

На рис. 282 предпринята попытка показать, как из гармонических колебаний отдельных частиц возле собственных равноотстоящих положений равновесия, возникает волна «сгустков и разряжений», распространяющаяся в направлении колебаний отдельных частиц. Здесь нарисованы одинаковые синусоиды (одна из них выделена), каждая из которых немного сдвинута относительно предыдущей (что соответствует сдвигу фаз между колебаниями соседних частиц). При наличии воображения на этом рисунке можно увидеть волну, которая движется в положительном направлении оси Ox (ось времени направлена вертикально вниз). Ниже отдельно изображены положения шариков в выделенные моменты времени.

В целом описание такой продольной волны не отличается от проведенного описания волны поперечной – она также описывается функцией (4), только смысл ее изменяется.

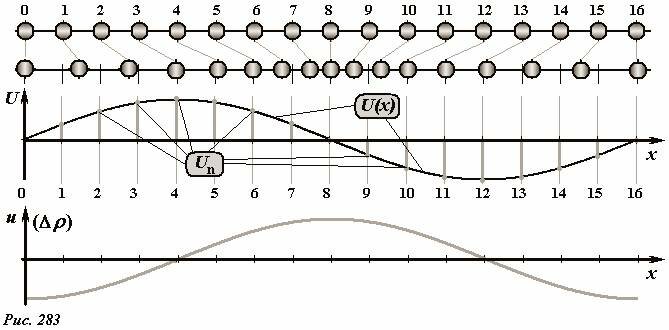
Для продольной волны, распространяющейся вдоль цепочки шариков, также может быть проведен переход к непрерывной струне. В таком пределе функция U(x,t) описывает смещение некоторой точки струны от ее положения равновесия – согласитесь, не очень наглядная величина. Чтобы сделать ее поле понятной внимательно ознакомьтесь с рис. 283: в верхнем ряду показана цепочка шариков в равновесном состоянии; второй ряд иллюстрирует положения шариков в некоторый момент времени бегущей волны; ниже в виде диаграммы изображены смещения шариков от их собственных положений равновесия U_n в этот же момент. Переход к непрерывной струне соответствует переходу к непрерывному графику зависимости смещения от координаты U(x).

Продольная волна, распространяющаяся по сплошной струне, может быть описана и другими характеристиками. Как уже неоднократно было отмечено, продольная волна представляет собой набор распространяющихся «сгустков и разряжений», в непрерывном пределе эти области отличаются концентрацией частиц (или плотностью струны). Эти области сжатия и растяжения возникаю из-за неравномерного смещения отдельных участков струны.

Совершим переход от функции смещения U(x) к плотности струны. Сначала рассмотрим случай дискретной цепочки. В этом случае под плотностью (или концентрацией) можно понимать среднее число частиц на единицу длины, поэтому в положении равновесия плотность цепочки равна

\(~\rho_0 = \frac{1}{l}\) . (14)

где l - расстояние между центрами соседних шариков (действительно: на длине l находится один шарик). При движении шариков плотность вблизи n-го шарика станет равной

\(~\rho = \frac{1}{X_{n+1}(t) - X_n(t)}\) , (15)

где

\(~\begin{matrix} X_{n+1}(t) = x_{n+1} + U_{n+1}(t) \\ X_n(t) = x_n + U_n(t) \end{matrix}\) (16)

координаты n-го и (n+1)-го шариков. Преобразуем выражение для плотности (15), считая, что смещения шариков значительно меньше расстояния между ними

\(~\rho = \frac{1}{X_{n+1}(t) - X_n(t)} = \frac{1}{l + U_{n+1}(t) - U_n(t)} = \frac{1}{l} \frac{1}{1 + \frac{U_{n+1}(t) - U_n(t)}{l}} \approx \frac{1}{l} \left(1 - \frac{U_{n+1}(t) - U_n(t)}{l} \right)\) . (17)

Последняя дробь представляет собой отношение разности смещений двух соседних частиц к разности их координат. При переходе к непрерывной струне (когда l → 0) эта дробь стремится к производной смещения по координате

\(~\frac{U_{n+1}(t) - U_n(t)}{l} \to \frac{\partial U}{\partial x}\) .

Эта производная называется частной, так как функция U(x,t) зависит от двух переменных. При вычислении производной по x вторая переменная t остается постоянной. Можно также считать, что мы вычисляем обычную производную от функции одной переменной U(x,t₀). Аналогично определяется частная производная по времени, которая вычисляется при постоянном значении x = x₀ = const. Физический смысл этой производной – скорость движения точки с координатой x₀.

Таким образом, плотность струны связана с функцией смещения соотношением

\(~\rho = \rho_0 \left(1 - \frac{\partial U}{\partial x} \right)\) . (18)

Если функция смещения описывается формулой (4), то изменение плотности описывается выражением

\(~u(x,t) = \rho - \rho_0 = -\rho_0 \frac{\partial U}{\partial x} = -\rho_0 \frac{\partial}{\partial x} (A \cos (\omega t - kx)) = \rho_0 Ak \sin (\omega t - kx)\) , (19)

то есть изменение плотности также изменяется вдоль струны с течением времени как гармоническая волна. Заметим, также, что изменение плотности максимально там, где смещение равно нулю. График зависимости плотности от координаты показан на рис. 283 снизу.

Полученная функция волны (4) зависит от двух переменных, поэтому ее графиком является двумерная поверхность. Эта поверхность может быть построена (Рис. 284). Однако, такое представление, на наш взгляд, не слишком удачно, так как мало наглядно. Конечно, рисунок можно воспринимать как набор профилей волны в последовательные моменты времени (последний профиль заштрихован), но для такого восприятия нужно иметь богатое воображение.

Рассмотренные нами волны являются механическими – они образуются благодаря механическому движению отдельных частиц среды. Существуют волны и другой физической природы. В среде могут периодически изменяться и другие ее характеристики, температура, концентрации частиц, электрическая поляризация, напряженность электрического поля, световые потоки и т.д. В таких волновых процессах изменяется физический смысл величины U(x,t), описывающей волну, при этом ее математическое описание остается неизменным.

Примечания

Следующая страница