Слободянюк А.И. Физика 10/19.4.I

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.4 Интерференция волн.

Многообразие волн, которое мы можем наблюдать вокруг нас, во многом связано с перекрытием простых волн. Явления, возникающие при наложении волн, называются интерференцией волн. Как будет показано в дальнейшем, эти явления проявляются в усилении или ослаблении амплитуды результирующей волны в зависимости от соотношения между фазами складывающихся в пространстве двух или нескольких волн одинаковых частот.

Разумеется, речь идет о сложении волн одной физической природы – описывать суперпозицию света и звука, не слишком логично.

Описание этого явления принципиально не отличается от описания суперпозиции электрических и магнитных полей. Однако, при «сложении» волн различной природы, прежде всего, необходимо обосновать возможность применения принципа суперпозиции. Напомним, что такое обоснование может быть дано только на основании физических законов, описывающих рассматриваемые волновые процессы. Так на основании линейности закона Гука мы показали, что этот принцип справедлив для упругих механических волн (в рамках применимости закона Гука).

Принцип суперпозиции справедлив для любых (в том числе и волновых) электромагнитных полей. В электродинамике математическим выражением принципа суперпозиции служит линейность уравнений Максвелла. Оказывается, что принципом суперпозиции можно пользоваться и для описания звуковых волн в газах, при не слишком большой амплитуде волн. Как мы уже неоднократно отмечали, поверхностные волны на воде приближенно подчиняются принципу суперпозиции только при небольших амплитудах.

Не смотря на то, что принцип суперпозиции не является универсальным для всех волн, здесь мы будем описывать интерференцию волн, основываясь на этом принципе. Взаимодействие волн, не подчиняющихся принципу суперпозиции, слишком сложное, нам хватит «сложностей» и при изучении интерференции «хороших» линейных волн.

Существенным отличием интерференции от суперпозиции стационарных полей является зависимость волновых полей от времени, поэтому результатом сложения волн также является волна, то есть процесс, изменяющийся во времени и в пространстве.

Так при наложении стационарных полей мы рассматривали их характеристики, изменяющиеся от одной пространственной точки к другой (но неизменные во времени), а при изучении сложения колебаний – складывали функции, изменяющиеся во времени, но происходящие в одной пространственной точке. Теперь нам необходимо объединить обе этих задачи – научиться складывать функции, зависящие как от времени, так и от пространственных координат.

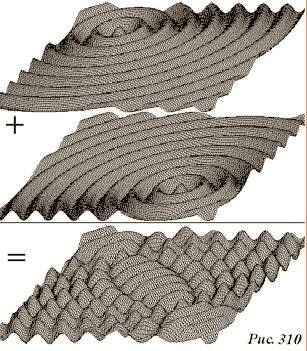
Наличие временных изменений приводит к тому, что результат наложения волн зависит не только от амплитуд интерферирующих волн, но и от разности фаз колебаний в данной точке. Эта «двойная зависимость» приводит к тому, что результирующая волна может существенно отличаться от своих составляющих. Так, например, на рис. 310 показан результат сложения двух одинаковых круговых волн – согласитесь, результат заметно отличается от двух семейств концентрических гребней.

Наличие разности фаз может приводить к тому, что в некоторых точках волны усиливают друг друга, а в некоторых полностью гасят друг друга.

Сформулируем общие условия, при которых мы будем описывать интерференцию волн. Первое. Рассматриваемые волны имеют одну физическую природу: интерферируют поверхностные волны с поверхностными, звуковые со звуковыми, электромагнитные с электромагнитными. Второе. Мы рассмотрим сложение монохроматических гармонических волн одинаковых частот. Только в этом случае образуется результирующая волна, такая, что амплитуды и фазы колебаний среды в различных точках не изменяются во времени. Третье. При сложении поперечных волн будем считать, что направления колебаний для всех волн одинаковы. В этом случае возмущение среды может быть описано скалярной функцией, зависящей от времени и пространственных координат \(~u(\vec r,t)\) .

Понятно, что складывать характеристики среды можно только в одной пространственной точке, поэтому интерференция волн возможна только в области перекрытия этих волн. Так если в некоторую точку пространства (положение которой задается радиус-вектором \(~\vec r\)) попадают несколько волн, описываемых функциями \(~u_n(\vec r,t)\), то суммарное возмущение среды в данной точке будет равно сумме возмущений, создаваемых каждой волной в отдельности (если, конечно справедлив принцип суперпозиции). Следовательно, математически описание интерференции волн сводится к вычислению сумм функций, описывающих отдельные волны

\(~U(\vec r,t) = \sum_n u_n(\vec r,t)\) . (1)

Монохроматическая волна в общем случае описывается функцией вида

\(~u_n(\vec r,t) = a_n(\vec r) \cos (\omega t + \varphi_n (\vec r))\) , (2)

где \(~a_n(\vec r)\) и \(~\varphi_n (\vec r)\) - амплитуды и фазы волн, соответственно, которые могут изменяться от точки к точке, но неизменны во времени. Ранее мы показали, что результатом сложения любого числа гармонических функций одной частоты является также гармоническая функция той же частоты. Поэтому при сложении любого числа монохроматических волн одной частоты будет монохроматическая волна той же частоты. Следовательно, при сложении волн, описываемых функциями вида (2), получается волна того же вида

\(~U(\vec r,t) = \sum_n a_n(\vec r) \cos (\omega t + \varphi_n (\vec r)) = A(\vec r) \cos (\omega t + \Phi (\vec r))\) . (3)

Таким образом, описание интерференции монохроматических волн сводится к вычислению амплитуды (при необходимости и фазы) результирующей волны. Договоримся об обозначениях: характеристики волн слагаемых будем обозначать малыми буквами с целочисленными индексами, характеристики результирующей волны теми же прописными буквами.

Процедуру сложения гармонических функций мы рассмотрели при изучении сложения колебаний (как и ранее здесь также очень удобным является метод векторных диаграмм), поэтому сейчас для нас наибольший интерес представляет пространственное распределение амплитуд результирующих колебаний среды.

Рассмотрим несколько примеров интерференции гармонических волн.

19.4.1 Интерференция волн от двух точечных источников.

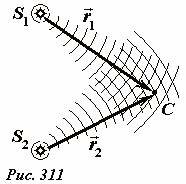
Пусть в некоторой области пространства перекрываются две волны, испущенные двумя идентичными точечными источниками S₁ и S₂ (Рис. 311). Так как источники точечные, то испущенные ими волны являются сферическими и описываются функциями

\(~u(r,t) = \frac{a_0}{\sqrt{r}} \cos (\omega t - kr)\) , (1)

где r - расстояние от источника до точки наблюдения, \(~k = \frac{2 \pi}{\lambda}\) - волновое число, одинаковое для обеих волн. В соответствии с принципом суперпозиции суммарное колебание в некоторой пространственной точке С равно сумме колебаний, создаваемых в этой точке каждой волной

\(~U(t) = u_1(r_1,t) + u_2(r_2,t) = \frac{a_0}{\sqrt{r_1}} \cos (\omega t - kr_1) + \frac{a_0}{\sqrt{r_2}} \cos (\omega t - kr_2)\) , (2)

где r₁, r₂ - расстояния от источников до точки наблюдения. Амплитуды колебаний достаточно медленно изменяются при изменении расстояния, поэтому для упрощения математических преобразований мы пренебрежем изменением амплитуд в области наблюдения интерференции, считая, что \(~\frac{a_0}{\sqrt{r_1}} \approx \frac{a_0}{\sqrt{r_2}} \approx a = \operatorname{const}\) (то есть будем полагать, что размеры этой области малы по сравнению расстояниями до источников). В этом приближении выражение (2) преобразуется к виду (при использовании тригонометрической формулы для суммы косинусов)

\(~U(t) = a \cos (\omega t - kr_1) + a \cos (\omega t - kr_2) = 2a \cos \left( \omega t - k \frac{r_1 + r_2}{2} \right) \cos \left( k \frac{r_1 - r_2}{2} \right)\) . (3)

Мы получили знакомый результат – сложение двух колебаний одинаковых амплитуд и частот приводит к колебанию той же частоты, амплитуда которого зависит от разности фаз исходных колебаний. Только в случае сложения волн разность фаз зависит от положения точки наблюдения, в результате чего амплитуда результирующего колебания изменяется при переходе от одной точки к другой. Зависимость амплитуды колебаний от координат точки наблюдения, как следует из формулы (3), имеет вид

\(~A(x,y,z) = 2a \left| \cos \left( k \frac{r_1 - r_2}{2} \right) \right|\) . (4)

Мы не случайно, выписали в явном виде координаты точки наблюдения как аргументы этой функции – расстояния от источников до точки наблюдения зависят координат последней. Кроме того, это выражение по модулю, так как изменение знака у амплитуды, соответствует изменению фазы на π. Очевидно, что амплитуда колебаний будет максимальна при выполнении условия

\(~k \frac{r_1 - r_2}{2} = \pi n, n = 0, \pm 1, \pm 2 \ldots\) . (5)

Подставляя значение волнового числа, получим

\(~\frac{2 \pi}{\lambda} \frac{r_1 - r_2}{2} = \pi n, n = 0, \pm 1, \pm 2 \ldots\)

или условие максимума интерференции имеет вид

\(~r_1 - r_2 = \lambda n, n = 0, \pm 1, \pm 2 \ldots\) (6)

разность хода двух волн равна целому числу длин волн.

Аналогично можно показать, что минимум интерференции будет наблюдаться, если

\(~r_1 - r_2 = \lambda \left( n + \frac{1}{2} \right), n = 0, \pm 1, \pm 2 \ldots\) (7)

разность хода равна полуцелому числу длин волн.

Полученные условия очевидны – максимум наблюдается в том случае, если гребень одной волны совпадает с гребнем другой; минимум - если гребень одной совпадает с впадиной другой, в этом случае волны равных амплитуд гасят друг друга.

Отметим еще одно обстоятельство, которое мы постоянно будем использовать в дальнейшем – при изменении разности хода волны на длину волны (например, при переходе от одного гребня к другому) фаза колебания изменяется на 2π.

Наконец, подчеркнем, что фазы колебаний в результирующей волне изменяются в пространстве достаточно хитрым образом, так, что результирующая волна не является не сферической и не плоской.

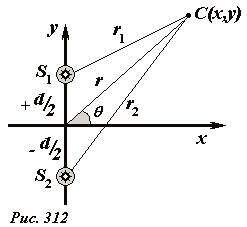
Продемонстрируем, что полученное выражение для амплитуды результирующего колебания действительно описывает ее пространственное распределение. Для этого введем декартовую систему координат, как показано на рис. 312: источники находятся на оси Oy симметрично относительно начала координат. Фигурирующие в формуле (4) расстояния от источников до произвольной точки С выражаются через ее координаты следующим образом

\(~\begin{matrix} r_1 = \sqrt{x^2 + \left( y - \frac{d}{2} \right)^2} \\ r_2 = \sqrt{x^2 + \left( y + \frac{d}{2} \right)^2} \end{matrix}\) , (8)

здесь обозначено d - расстояние между источниками. Окончательно, пространственное распределение амплитуд описывается очень громоздкой формулой

\(~A(x,y,z) = 2a \left| \cos \left( k \frac{r_1 - r_2}{2} \right) \right| = 2a \left| \cos \left( \frac{\pi}{\lambda} \left( \sqrt{x^2 + \left( y - \frac{d}{2} \right)^2} - \sqrt{x^2 + \left( y + \frac{d}{2} \right)^2} \right) \right) \right|\) . (9)

В данном выражении амплитуда зависит только от двух координат в рассматриваемой плоскости xOy. Такой результат получается для поверхностных волн. Если же рассматриваются сферические волны в трехмерном пространстве, то вследствие очевидной осевой симметрии, полученную «картинку» следует мысленно вращать вокруг оси Oy. Конечно, представить себе поверхность, описываемую функцией (9) очень сложно, но можно построить ее с помощью компьютера. На рис. 313 показан трехмерный график зависимости амплитуды результирующего колебания от координат точки наблюдения. График построен при d = 3,2 λ.

А теперь скажем, что в принципе полученный график понятен. Условие максимума интерференции (8) утверждает, что максимумы амплитуды расположены в точках, где разность расстояний до источников равна целому числу длин волн, то есть является постоянно. А это ничто иное, как классическое определение гиперболы. Таким образом, гребни (как и впадины) этой функции образуют гиперболы (или гиперболоиды вращения в трехмерном пространстве).

Полученный график демонстрирует пространственное распределение амплитуды колебаний, а не профиль волны в некоторый момент времени – потому, что фазы колебаний различны в разных точках (в одних максимум, в других минимум, в третьих что-то среднее). Профиль волны описывается еще более сложной функцией (3), в которой следует задать определенное значение момента времени t. Для примера на рис. 314 показан такой профиль при t = 0.

При определенных навыках и эту поверхность можно понять. Из формулы (3) следует, что фаза колебаний результирующей волны

\(~\Phi(x,y) = k \frac{r_1 + r_2}{2}\)

постоянна в тех точках, для которых сумма расстояний до источников постоянна \(r_1 + r_2 = \operatorname{const}\). Геометрическое место этих точек является эллипсом. Следовательно, фазовыми поверхностей является семейство эллипсов, фокусы которых совпадают с источниками волн. Поэтому результирующую волну можно представить как расходящуюся эллиптическую волну

\(~U(x,y,t) = 2a \cos \left( \omega t - k \frac{r_1 + r_2}{2} \right)\)

(на рис. 315 показана такая волна, только с неизменной амплитудой), амплитуда которой изменяется в соответствии с формулой (4). Мысленно перемножьте графики 313 и 314 – получите рисунок 314.

Может и не слишком понятно, но зато рисунки красивые – не правда ли?

Обратимся еще раз к формуле (4) и рассмотрим распределение амплитуды результирующего колебания в точках, расстояние до которых значительно больше расстояния между источниками d << r₁, r₂, в так называемой, волновой зоне. В этом случае положение точки наблюдение удобно задавать с помощью полярных координат: r - расстояния до начала координат, угла θ между направлением на данную точку и осью Ox (они указаны на рис. 312).

В этом приближении формулу (4) можно упростить. Для этого используем теорему косинусов для треугольников OCS₂ и OCS₁:

\(~\begin{matrix} r^2_2 = r^2 + \left( \frac{d}{2} \right)^2 - 2r \frac{d}{2} \cos \left( \frac{\pi}{2} + \theta \right) = r^2 + \left( \frac{d}{2} \right)^2 + r d \sin \theta \\ r^2_1 = r^2 + \left( \frac{d}{2} \right)^2 - 2r \frac{d}{2} \cos \left( \frac{\pi}{2} - \theta \right) = r^2 + \left( \frac{d}{2} \right)^2 - r d \sin \theta \end{matrix}\) .

Теперь вычислим разность этих выражений

\(~r^2_2 - r^2_1 = (r_2 - r_1)(r_2 + r_1) = 2 r d \sin \theta\) .

В рассматриваемом приближении расстояния r₁, r₂ различаются мало, поэтому можно положить \((r_2 + r_1) \approx 2r\), тогда разность расстояний до источников приближенно равна

\(~(r_2 - r_1) = d \sin \theta\) . (10)

Сделанное при выводе этой формулы приближение, равносильно пренебрежению малыми величинами второго \(~\left( \frac{d}{r} \right)^2\) и более высоких порядков.

Докажите это утверждение самостоятельно, используя приближенную формулу для квадратного корня \(~\sqrt{1 + \xi} \approx 1 + \frac{1}{2} \xi - \frac{1}{8} \xi^2\).

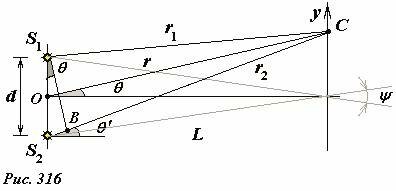
Использованное приближение можно также проиллюстрировать геометрически (Рис. 316). Проведем отрезок S₁B, перпендикулярный прямой OC, соединяющий центр излучающей системы с точкой наблюдения. В полученном треугольнике BS₁S₂ угол BS₁S₂ равен θ. Если точка наблюдения С находится на большом расстоянии от излучателей, то прямые S₁C, OC, S₂C очень близки к параллельным, поэтому угол S₁BS₂ близок к прямому. Поэтому разность хода волн от источников до точки наблюдения может быть найдена из «почти прямоугольного» треугольника BS₁S₂

\(~(r_2 - r_1) = |S_2 B| \approx d \sin \theta\) ,

что совпадает с формулой полученной ранее.

Кому не очень нравятся «параллельные» прямые, пересекающиеся в одной точке, может утверждать, что пир геометрическом выводе используется приближенное равенство углов (см. рис) θ′ =θ. Тем не менее, в физике для обозначения рассматриваемой системы (и рассматриваемого приближения) часто используется не очень удачные термин – «интерференция параллельных лучей».

Используя простую формулу (1) для разности хода, получим что, в волновой зоне распределение амплитуд (4) зависит только от направления на точку наблюдения и описывается формулой

\(~A(\theta) = 2a \left| \cos \left( \frac{1}{2} k \sin \theta \right) \right| = 2a \left| \cos \left( \pi \frac{d}{\lambda} \sin \theta \right) \right|\) . (11)

То есть, два источника испускаю волну, которая распространяется только в определенных направлениях, Направления максимумов испускания удовлетворяют условию

\(~\pi \frac{d}{\lambda} \sin \theta = \pi n\) ,

или

\(~d \sin \theta_{max,n} = n \lambda\) , (12)

где индекс n указывает номер максимума.

Направления, в которых амплитуда обращается в нуль, удовлетворяет условию

\(~d \sin \theta_{min,n} = \left( n + \frac{1}{2} \right) \lambda\) . (13)

Полученным соотношениям придадим еще одну интересную форму. Рассмотрим распределение амплитуды суммарной волны вдоль прямой, параллельной источников, находящейся на расстоянии L от них (на рис. 316 она обозначена, как ось y). Координаты точек на этой оси, в которых амплитуда волны максимальна, равны (с учетом формулы (12))

\(~y_{max,n} = L \sin \theta_{max,n} = \frac{L \lambda}{d} n\) (14)

и отстоят друг от друга на равном расстоянии \(~\Delta y = \frac{L \lambda}{d}\) друг от друга – отметим, что это расстояние называется шириной интерференционной полосы. Наконец заметим, что отношение расстояния между источниками к расстоянию до точек наблюдения \(~\frac{d}{L} \approx \Psi\) равно углу ψ, под которым видны источники с точки наблюдения. Этот же угол образуют волновые векторы интерферирующих волн \(~\vec k_1\), \(~\vec k_2\) , указывающие направления распространения волн. Таким образом, ширина интерференционной волны равна отношению длины волны к углу схождения волн

\(~\Delta y = \frac{L \lambda}{d} = \frac{\lambda}{\Psi}\) . (15)

Вернемся еще раз к формуле (12), определяющие направления, в которых амплитуда излучения максимальна. Количество этих направлений зависит от отношения расстояния между источниками к длине испускаемой волне (не забывайте - значение косинуса не превосходит по модулю 1). На рис. 317 показано пространственное распределение амплитуд. Рисунок иллюстрирует наличие направлений максимального излучения волн.

Эти направления можно изменять, задавая начальную разность фаз колебаний источников, кроме того, максимумы интенсивности можно сделать более резкими, если увеличить число источников. На этом интерференционном принципе формирования и управления направлением излучения работают современные фазовые решетки радиолокационных станций (РЛС).

Примечания

Следующая страница