Слободянюк А.И. Физика 10/2.12
§2. Кинематическое описание механического движения материальной точки
2.12 Относительность движения
Когда мы рассуждали о координатах, мы подчеркивали, что указание координат имеет смысл только тогда, когда указана, задана система координат. Поэтому координаты точки являются относительными физическими величинами. Поэтому относительными являются и изменения координат с течением времени, иными словами относительным является само механическое движение [1]. Выбор системы координат, в принципе, произволен и определяется главным образом удобством описания, или личными вкусами исследователя - так, например, некоторым приятно описывать свое движение среди неподвижных звезд. Отсутствие единой, всеобщей системы координат приводит к тому, что все системы отсчета являются равноправными, движение в разных системах отсчета должно описываться принципиально одинаково. Мы, конечно, не утверждаем, что уравнения движения будут одинаковы во всех системах отсчета, в одних они будут проще, в других сложнее, но методы описания, его результаты должны быть одинаковы - так если два тела должны столкнуться в одной системе отсчета, то такой же результат должен быть и в другой системе. Реально, в природе существуют материальные тела, которые движутся, взаимодействуют, видоизменяются - а наше описание движения в конкретных системах отсчета является всего лишь попыткой построить его более-менее приличную модель. Согласование описания движения, переход из одной системы координат в другую является очень важной физической задачей, далеко выходящей за рамки проблем кинематики. В данном параграфе мы рассмотрим эту проблему только с точки зрения кинематического описания. Для простоты и удобства графических иллюстраций мы будем изображать системы координат на плоскости, обобщение на случай трехмерного пространства очевидно, а при векторной записи остается тем же самым, кроме того, будем полагать, что соответствующие оси координат параллельны. Произвольная ориентация координат, добавляет не много физического содержания, а математическое описание становится более громоздким.
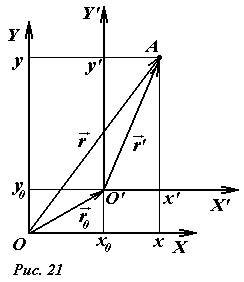
Рассмотрим две системы координат [2] : исходную XOY, и смещенную X’O’Y’ (рис. 21). Координаты начала отсчета смещенной системы координат в исходной системе обозначим O’, а радиус-вектор этой точки \(~\vec r_0\) . Тогда связь между координатами материальной точки A в этих системах определяется формулами
которые можно записать в компактной векторной форме
Эти формулы очевидны для неподвижных систем отсчета и неподвижных тел, сейчас нам необходимо обобщить их на случай описания движения. То есть нам из системы координат необходимо сделать систему отсчета, добавив в каждую из них часы. У нас пока нет никаких оснований считать, что одинаковые часы в разных системах отсчета будут идти по-разному. Поэтому будем полагать, что время в разных системах отсчета одинаково и начала отсчета времени также совпадают
Пусть точка A движется с некоторой скоростью \(~\vec \upsilon\ ' = \frac{\Delta \vec r\ '}{\Delta t}\) относительно смещенной системы координат. Найдем скорость точки в исходной системе отсчета XOY. Для этого воспользуемся формулой (2):
при выводе мы учли, что вектор \(~\vec r_0\) является постоянным и его изменение равно нулю. Таким образом, мы показали, что при переходе из одной неподвижной системы отсчета в другую скорость точки не изменяется. Впрочем, этот результат очевиден - течение времени и перемещение точек одинаковы в обеих системах отсчета. Если скорости точек не изменяются, то не будут изменяться и их ускорения, так они выражаются через изменение скоростей.
Пусть система X’O’Y’ движется относительно системы XOY с постоянной скоростью \(~\vec V\). В любой момент времени соотношения между координатами выражаются соотношениями (1)-(2). В случае движущейся системы координат, мы не можем логически строго утверждать, что течение времени будет таким же, как и в неподвижной системе. Вопрос о том, изменится ли ход часов, если они будут двигаться с постоянной скоростью, не может быть разрешен путем логических рассуждений. Ответ на него может дать только эксперимент, только опыт. Мы еще не раз будем возвращаться к этой проблеме, тока же примем как аксиому, подтвержденную многовековым опытом человечества, что течение времени одинаково в различных системах отсчета, движущихся друг относительно друга с постоянной скоростью.
Найдем соотношение между скоростями точки в подвижной [3] X’O’Y’ и неподвижной XOY системах координат. Опять воспользуемся соотношением (2) для вычисления скорости в неподвижной системе отсчета
легко заметить, что \(~\frac{\Delta \vec r_0}{\Delta t} = \vec V\) - скорость движения подвижной системы, а \(~\frac{\Delta \vec r\ '}{\Delta t} = \vec \upsilon\ '\) - скорость точки относительно подвижной системы координат. Довольно часто применяется следующая терминология: Скорость точки относительно подвижной системы координат \(~\vec \upsilon\ '\) называют относительной скоростью, скорость точки относительно неподвижной системы координат называют абсолютной скоростью, а скорость одной системы координат относительно другой называю переносной скоростью. Используя эти названия, очень важное соотношение (5) можно словесно сформулировать в виде:
Абсолютная скорость точки равна сумме ее относительной скорости и переносной скорости.
Из соотношения (5) можно выразить относительную скорость
относительная скорость точки равна разности между ее абсолютной скоростью и переносной скоростью.
Заметьте, что соотношению (6) можно дать и другое истолкование. Будем считать систему отсчета X’O’Y’ неподвижной, а систему XOY подвижной. Тогда переносная скорость (то есть скорость системы XOY относительно X’O’Y’) будет равна \(~(-\vec V)\) , поэтому соотношение (6) просто совпадает с формулой (5).
Подведем итог: при равномерном движении системы X’O’Y’ со скоростью \(~\vec V\) относительно системы XOY радиус-вектор начала отсчета подвижной системы изменяется по закону \(~\vec r_0 = \vec V t\) , поэтому координаты точки и времена в этих системах отсчета связаны соотношениями
Эти преобразования называются преобразования Г. Галилея, и играют чрезвычайно важную роль в классической физике.
Соотношения между скоростями (5)-(6) выполняются в любой момент времени, поэтому их можно использовать для того, чтобы установить связь между ускорениями точек в различных системах координат. Пусть точка A движется с ускорением \(~\vec a'\) относительно подвижной системы координат (будем по-прежнему считать, что переносная скорость является постоянной), тогда ее ускорение в неподвижной системе можно вычислить по следующим формулам
Мы доказали, что если одна система движется относительно другой с постоянной скоростью, то ускорения тел относительно этих систем отсчета одинаковы. Иными словами, ускорение является инвариантной величиной при переходе из одной системы отсчета в другую.
Наше изложение можно продолжить в том же духе - рассмотреть случай ускоренного движения одной системы относительно другой. Однако сейчас мы не будем заниматься этим, так как при изучении динамики мы увидим, что системы движущиеся друг относительно друга равномерно и прямолинейно занимают особое место в механике, именно им уделяется особое внимание, на что есть весьма серьезные физические причины.
Примечания
- ↑ Относительность движения можно понимать в нескольких смыслах. Во-первых, тело покоящееся в одной системе отсчета может двигаться относительно другой системы. Во-вторых, кинематические характеристики движения - координаты, скорость, ускорение зависят от системы отсчета. Говоря об относительности движения, будем подразумевать именно второй его смысл.
- ↑ Напомним, что названия «исходная» и «смещенная» условны - ничего не изменится, если их поменять местами.
- ↑ Очередной раз отметим условность названий систем отсчета - если одна система движется относительно другой, то справедливо и обратное - выбор неподвижной и движущейся систем остается за исследователем.
