Слободянюк А.И. Физика 10/2.7

Содержание книги

Предыдующая страница

§2. Кинематическое описание механического движения материальной точки

2.7 Равноускоренное движение точки по прямой

Пусть материальная точка движется вдоль заданной прямой линии так, что ее ускорение остается постоянным. Такое движение точки называется равноускоренным или равнопеременным движением. По-прежнему, направим ось X вдоль прямой, по которой движется точка, и введем обычным образом координаты на этой прямой.

Используя определение ускорения

\(~a = \frac{\upsilon - \upsilon_0}{t - t_0} = \frac{\Delta \upsilon}{\Delta t}\) (1)

и учитывая, что при постоянном ускорении это отношение не зависит от значения интервала времени, мы можем выразить значение скорости в произвольный момент времени t

\(~\upsilon = \upsilon_0 + a (t - t_0)\) . (2)

Это выражение определяет скорость как функцию времени. Как следует из полученного уравнения, зная только ускорение, нельзя однозначно определить скорость в произвольный момент времени. Для этого необходимо задать дополнительное условие: скорость υ₀ в некоторый момент времени t₀. Часто это условие называют начальным и, полагая t₀ = 0 , называют величину υ₀ начальной скоростью.

Графиком зависимости скорости от времени при равноускоренном движении (то есть графиком функции (2)) является прямая линия, проходящая через точку A с координатами (t₀,υ₀), коэффициент наклона которой равен ускорению точки (рис.15).

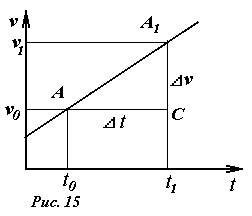
Как было показано ранее площадь под графиком зависимости скорости от времени равна изменению координаты точки. Воспользуемся этим правилом, для того чтобы решить основную задачу кинематики - найти закон движения - для равноускоренного движения. Изменение координаты Δx в данном случае численно равно площади трапеции t₀t₁A₁A, которая вычисляется как произведение полусуммы оснований на высоту

\(~\Delta x = \frac{\upsilon_0 + \upsilon_1}{2} \cdot (t_1 - t_0) = \frac{\upsilon_0 + \upsilon_0 + a (t_1 - t_0)}{2} \cdot (t_1 - t_0) = \upsilon_0 (t_1 - t_0) + \frac{a (t_1 - t_0)^2}{2}\) . (3)

При выводе этого соотношения мы учли, что \(~\upsilon_1 = \upsilon_0 + a (t_1 - t_0)\) . При равноускоренном движении полученное соотношение справедливо для любого момента времени t₁, поэтому вместо конкретного значения t₁ можно подставить переменную величину - текущее время. Изменение координаты по определению равно Δx = x - x₀ , следовательно, закон движения имеет вид

\(~x = x_0 + \upsilon_0 (t - t_0) + \frac{a (t - t_0)^2}{2}\) . (4)

В той формуле x₀ - координата, а υ₀ - скорость в момент времени t₀. Часто эти параметры называют начальными. Обратите внимание, чтобы найти закон движения при постоянном ускорении, помимо значения ускорения необходимо задать два дополнительных условия - координату и скорость в некоторый момент времени. Закон движения (4) можно использовать не только для t > t₀, но и для любые других моментов времени, если конечно вы уверены, что в эти моменты характер движения не изменялся.

Вернемся к цепочке преобразований (3). Из уравнения (2) следует \(~t - t_0 = \frac{\upsilon_1 - \upsilon_0}{a}\) . Подставим это выражение в формулу (3)

\(~\Delta x = \frac{\upsilon_0 + \upsilon_1}{2} \cdot (t_1 - t_0) = \frac{\upsilon_0 + \upsilon_1}{2} \cdot \frac{\upsilon_1 - \upsilon_0}{a} = \frac{\upsilon^2_1 - \upsilon^2_0}{2a}\) . (5)

Мы получили важное соотношение, позволяющее найти изменение координаты тела по известным ускорению, начальной и конечной скоростям. Так, например, тормозной путь автомобиля S может быть легко подсчитан по этой формуле: полагая конечную скорость равной нулю и, учитывая, что при торможении ускорение отрицательно a = -|a| , из формулы (5) следует, что \(~S = \frac{\upsilon^2_0}{2a}\) .

Рассмотрим подробнее характер движения при различных значениях параметров равноускоренного движения. Выбор начала отсчета времени, как и выбор начала отсчета координаты произволен, поэтому при изучении движения одного тела, мы можем положить t₀ = 0 и x₀ = 0. Таким образом рассмотрим закон движения в форме

\(~x =\upsilon_0 t + \frac{a t^2}{2}\) . (6)

При этом скорость тела изменяется по закону

\(~\upsilon = \upsilon_0 + a t\) . (7)

Удобно одновременно исследовать обе функции - зависимости от времени скорости и координаты. С графиками функции (7) мы уже познакомились - это прямые линии. В общем случае координата зависит от времени по квадратичному закону, поэтому графиком этой функции является парабола.

Рассмотрим несколько частных случаев.

1. Начальная скорость υ₀ = 0. В этом случае исследуемые функции имеют вид \(~\upsilon =a t , x =\frac{a t^2}{2}\)

   

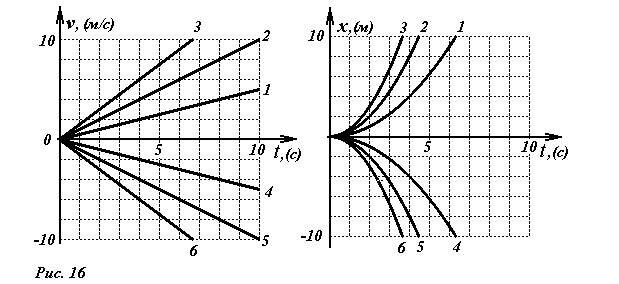
   Прямые зависимостей υ(t) проходят через начало координат, вершины парабол зависимостей x(t) совпадают с началом координат (естественно, своих). Увеличение ускорения приводит к увеличению коэффициента наклона прямой υ(t), и увеличению крутизны парабол x(t). При отрицательном значении ускорения наклон прямых υ(t) становится отрицательным, а ветви парабол x(t) опускаются вниз.

   На рис.16 показаны описанные зависимости для значений ускорения 0,5 м/с², 1,0 м/с², 1,5 м/с² (графики 1,2,3) и отрицательных ускорений -0,5 м/с², -1,0 м/с², -1,5 м/с²(графики 4,5,6).

2. Положительное ускорение a > 0, начальная скорость отлична от нуля υ₀ ≠ 0.

   

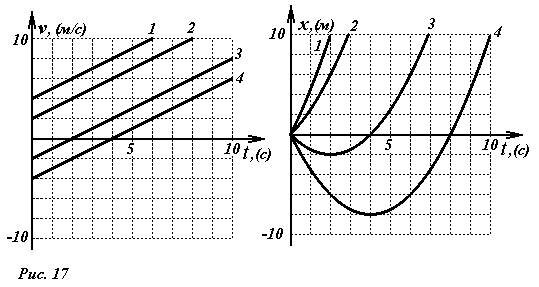
   График зависимости скорости от времени имеет вид прямой (рис.17). Значение начальной скорости равно длине отрезка, который отсекает график на оси скорости. График зависимости координаты от времени является параболой, ветви которой направлены вверх, проходящей через начало координат. Проведем касательную к этой параболе в начальной точке. Как мы показали ранее, коэффициент наклона касательной равен мгновенной скорости. В момент времени t = 0 коэффициент наклона касательной, следовательно, совпадает с начальной скоростью υ₀. Если начальная скорость положительна, то парабола стремится вверх.

   Рассмотрим теперь случай, когда ускорение осталось прежним a > 0 , но начальная скорость отрицательна υ₀ < 0. В этом случае прямая зависимости υ(t) «стартует» с отрицательных значений скорости. Поэтому касательная к параболе зависимости x(t) в начальный момент имеет отрицательный наклон, хотя ветви параболы по-прежнему направлены вверх. До тех пор пока скорость отрицательна, координата убывает, достигая минимального значения в момент времени, когда скорость становится равной нулю. Это и понятно и с точки зрения здравого смысла: пока скорость отрицательна, точка движется в отрицательном направлении оси, как только скорость становится положительной, точка начинает двигаться в противоположном направлении, следовательно, в момент времени, когда υ = 0, точка находилась на максимальном удалении от начала отсчета. Это утверждение является универсальным правилом - если скорость точки изменяет знак, то в момент времени, когда скорость равна нулю, точка находится в своем крайнем положении (координата минимальна или максимальна).

   Посмотрите, как изменяются графики зависимостей скорости и координаты при изменении начальной скорости. На рис. 17 построены зависимости υ(t) и x(t) при одинаковом ускорении a = 1,0 м/с², но при разных начальных скоростях. Заметьте, что прямые υ(t) параллельны, а все параболы x(t) одинаковы - они отличаются только положением вершины.

Другие комбинации начальных параметров можно рассмотреть аналогично - в частности, случай a > 0, υ₀ ≠ 0 является зеркальным отражением только что рассмотренной ситуации - его можно свести к рассмотренному варианту, просто изменив направление оси X.

Итак, мы рассмотрели еще одну модель - равноускоренное движение. Надо отметить, что движение, близкое к равноускоренному, довольно часто встречается в окружающем нас мире. Так, если тело движется под действием постоянных сил, то его движение является равноускоренным. Например, свободное падение массивных тел, скатывание шара с наклонной плоскости - примеры такого движения.

Тем не менее, модель равноускоренного движения также является приближенной. Если в названных примерах сопротивление воздуха играет существенную роль, то ускорение тел будет заметно изменяться, поэтому модель равноускоренного движения окажется неприменимой.

Примечания

Следующая страница