Слободянюк А.И. Физика 10/3.6
§3. Криволинейное движение. Плоскопараллельное движение твердого тела
3.6 Плоскопараллельное движение
Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.
Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.
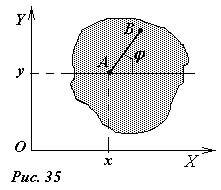
Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела [1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.
Выберем внутри тела две точки A, B; зададим координаты xA, yA точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа xA, yA и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.
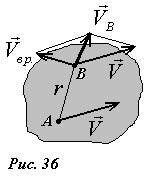
Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).
Разложим движение на две составляющих - поступательное движение, скорость которого обозначим \(~\vec V\) , и вращение вокруг оси, проходящей через точку A, с угловой скоростью \(~\omega = \frac{\Delta \varphi}{\Delta t}\) . Тогда скорость любой другой точки тела (например, B) является векторной суммой скоростей поступательного и вращательного движений -
причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине VBP = ωr, где r расстояние от точки B до оси вращения.
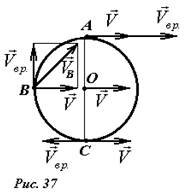
Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).
Пусть его центр движется со скоростью \(~\vec V\). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой \(~\omega = \frac{\upsilon}{R}\). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому \(~V_{BP} = \omega r = \frac{V}{R} R = V\) . Однако, направление этой скорости различно для разных точек. Так, для точки A скорость вращательного движения направлена горизонтально, также как и скорость поступательного движения. Поэтому суммарная скорость точки A равна 2V и направлена горизонтально. Скорость вращательного движения точки B направлена вертикально вверх, поэтому ее полная скорость направлена под углом 45° к горизонту, а ее модуль \(~V_B = V \sqrt{2}\) . Очень интересна точка касания с поверхностью C : скорость ее вращательного движения направлена горизонтально в сторону противоположную скорости поступательного движения, поэтому ее полная скорость равна нулю.
Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.
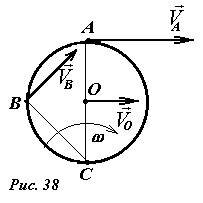
Легко доказать, что угол поворота тела не зависит от того, относительно какой оси мы его рассматриваем, следовательно, и угловая скорость не зависит от оси. С этой точки зрения, скорость любой точки колеса определяется формулой V = ωr’ , где r’ - расстояние от данной точки до мгновенной оси вращения.
Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна VA = 2Rω = 2V; точка B находится на расстоянии \(~R \sqrt{2}\) от оси, ее скорость \(~V \sqrt{2}\). Направления векторов скоростей также совпадают с полученными ранее.
Таким образом, мы имеем два примерно одинаковых по сложности способа описания движения твердого тела: первый - суперпозиция поступательного и вращательного движений: второй - поворот вокруг мгновенной оси.
Примечания
- ↑ С точки зрения кинематического описания выбор этой точки произволен - только следует стремиться к тому, чтобы траектория этой точки была попроще. Далее мы укажем как можно легко найти такую точку.