Слободянюк А.И. Физика 10/6.10
Материал из PhysBook
§6. Законы сохранения в механике
6.10 Заметки о симметрии.
Хотя в физике очень много сложного, в ней также много простоты и изящества, что в значительной мере обусловлено симметрией физических законов и систем. В соответствии с этим симметрия не только занимает важное место в физике, но и играет все возрастающую роль в современных физических исследованиях.
Симметрия в широком смысле – свойство геометрической фигуры, характеризующее некоторую правильность формы, неизменность ее при движениях и зеркальных отображениях.
Рассмотрим некоторые виды и элементы симметрии.
-
Симметрия относительно плоскости (зеркальная симметрия) .
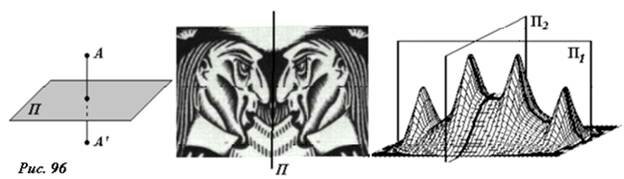
- Две точки A и A’ симметричны относительно плоскости П, если они расположены на одном перпендикуляре к плоскости и на равном расстоянии от нее (рис. 96). Фигуры и тела симметричны относительно плоскости, если для каждой точки тела, существует симметричная относительно плоскости другая точка тела. Плоскостью симметрии могут обладать как плоские, так и объемные фигуры. Тела могут обладать и несколькими плоскостями симметрии, так фигура, показанная на рисунке, обладает двумя плоскостями симметрии. Если ввести декартовую ось координат Z, перпендикулярную плоскости симметрии, то любая характеристика системы будет сохраняться при изменении знака этой координаты F(x,y,z) = F(x,y,-z).
-
Оси симметрии.
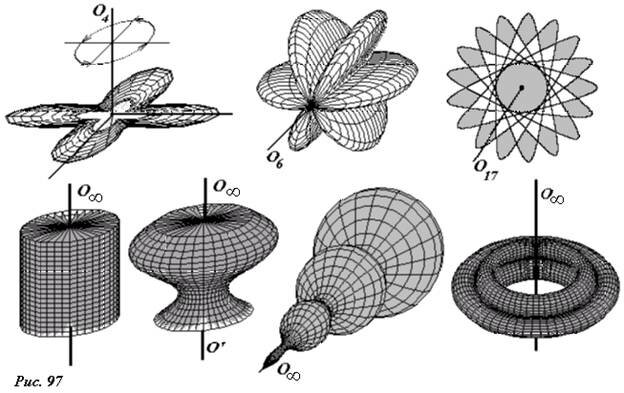
- Тело обладает осью симметрии n-го порядка On, если при вращении вокруг этой оси, тело n раз совмещается с самим собой (рис. 97).
- Если фигура совмещается сама с собой при повороте на любой угол, то такое тело называется осесимметричным, а прямая, вокруг которой можно проводить поворот на любой угол без изменения формы фигуры, называется осью симметрии. Формально ось симметрии можно рассматривать как ось симметрии бесконечного порядка \(~O_{\infty}\) .
- Простейшей пространственной фигурой, обладающей осью симметрии, является цилиндр, поэтому такой тип симметрии также называют цилиндрической симметрией. Заметим, что любая плоскость, содержащая ось симметрии, является плоскостью симметрии.
-
Сферическая (центральная) симметрия.
- Тело обладает центром симметрии, если любая прямая проходящая через центр, является осью симметрии. Иными словами, тело можно повернуть на любой угол относительно любой прямой, проходящей через центр симметрии. Такой симметрией обладает сфера (чем и обусловлено ее название). Любая характеристика системы, обладающей сферической симметрией, зависит только от расстояния до центра. Так сила гравитационного притяжения между точечными телами зависит только от расстояния между телами, поэтому говорят, что эта сила сферически симметрична.
-
Трансляционные симметрии.
- Этот вид симметрии связан с восстановлением тел при их смещении. Понятно, что такими видами симметрии обладают только бесконечно большие тела. В некоторых случаях системы повторяют себя строго определенных смещениях. Так для бесконечной плоскости, покрытой рисунками (рис. 98), при ее смещении на векторы \(~\vec A = k_x \vec a_x + k_y \vec a_y\) (где kx, ky - любые целые числа) происходит ее совмещение с начальным положением. Такой вид симметрии присущ кристаллам, поэтому его изучение играет важную роль в кристаллографии.
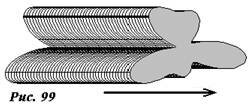
- Некоторые системы повторяют себя при смещении на произвольное расстояние в определенном направлении. Таким свойством обладает, например, бесконечно длинный прямой цилиндр произвольного сечения (рис. 99). Для однородной плоскости, восстановление происходит при смещении на любой расстояние вдоль любого вектора, параллельного плоскости.
- Наконец, в однородном веществе, можно провести сдвиг в любом направлении на любое расстояние.
Симметрии реальных физических систем обладают свойством «самосохранения», так если источники (света, электрические заряды и т.д.) обладают какой либо симметрией, то такой же симметрией обладают и результаты действия этих источников.