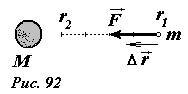Слободянюк А.И. Физика 10/6.7
§6. Законы сохранения в механике
6.7 Потенциальная энергия гравитационного притяжения.
Все тела, обладающие массой, притягиваются друг к другу с силой, подчиняющейся закону всемирного тяготения И.Ньютона. Следовательно, притягивающиеся тела обладают энергией взаимодействия.
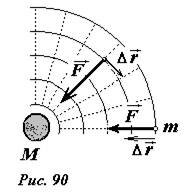
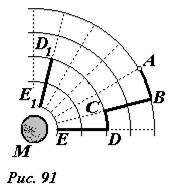
Покажем, что работа гравитационных сил не зависит от формы траектории, то есть гравитационные силы также являются потенциальными. Для этого рассмотрим движение небольшого тела массой m, взаимодействующего с другим массивным телом массы M, которое будем полагать неподвижным [1] (рис. 90). Как следует из закона Ньютона сила \(~\vec F\) , действующая между телами, направлена вдоль линии, соединяющей эти тела. Поэтому при движении тела m по дуге окружности с центром в точке, где находится тело M, работа гравитационной силы равна нулю, так как векторы сил и перемещения все время остаются взаимно перпендикулярными. При движении вдоль отрезка, направленного к центру тела M, векторы перемещения и силы параллельны, поэтому в этом случае при сближении тел работа гравитационной силы положительна, а при удалении тел – отрицательна. Далее заметим, что при радиальном движении работа силы притяжения зависит только от начального и конечного расстояния между телами. Так при движении по отрезкам (см. рис.91) DE и D1E1 совершенные работы равны, так как законы изменения сил от расстояния на обоих отрезках одинаковы. Наконец, произвольную траекторию тела m можно разбить на набор дуговых и радиальных участков (например, ломаная ABCDE). При движении по дугам работа равна нулю, при движении по радиальным отрезкам работа не зависит от положения этого отрезка – следовательно, работа гравитационной силы зависит только от начального и конечного расстояния между телами, что и требовалось доказать.
Заметьте, что при доказательстве потенциальности мы воспользовались только тем фактом, что гравитационные силы являются центральными, то есть направленными вдоль прямой, соединяющей тела, и не упоминали о конкретном виде зависимости силы от расстояния. Следовательно, все центральные силы являются потенциальными.
Мы доказали потенциальность силы гравитационного взаимодействия между двумя точечными телами. Но для гравитационных взаимодействий справедлив принцип суперпозиции – сила, действующая на тело со стороны системы точечных тел, равна сумме сил парных взаимодействий, каждая из которых является потенциальной, следовательно, и их сумма также потенциальна. Действительно, если работа каждой силы парного взаимодействия не зависит от траектории, то и их сумма также не зависит от формы траектории. Таким образом, все гравитационные силы потенциальны.
Нам осталось получить конкретное выражение для потенциальной энергии гравитационного взаимодействия.
Для вычисления работы силы притяжения между двумя точечными телами достаточно подсчитать эту работу при движении вдоль радиального отрезка при изменении расстояния от r1 до r2 (рис. 92).
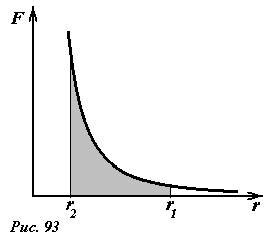
Очередной раз воспользуемся графическим методом, для чего построим зависимость силы притяжения \(~F = G \frac{mM}{r^2}\) от расстояния r между телами, тогда площадь под графиком этой зависимости в указанных пределах и будет равна искомой работе (рис. 93). Вычисление этой площади представляет собой не слишком сложную задачу, требующее, однако, определенных математических знаний и навыков. Не вдаваясь в детали этого расчета, приведем конечный результат, для данной зависимости силы от расстояния площадь под графиком, или работа силы притяжения определяется формулой
Так как мы доказали, что гравитационные силы являются потенциальными, эту работу равна уменьшению потенциальной энергии взаимодействия, то есть
Из этого выражения можно определить выражение для потенциальной энергии гравитационного взаимодействия
При таком определении потенциальная энергия отрицательна и стремится к нулю при бесконечном расстоянии между телами \(~U(\infty) = 0\) . Формула (1) определяет работу, которую совершит сила гравитационного притяжения при увеличении расстояния от r до бесконечности, так как при таком движении векторы силы и перемещения направлены в противоположные стороны, то эта работа отрицательна. При противоположном движении, при сближении тел от бесконечного расстояния до расстояния , работа силы притяжения будет положительна. Эту работу можно подсчитать по определению потенциальной энергии \(~A_{\infty \to r}U(r) = - (U(\infty)- U(r)) = G \frac{mM}{r}\) .
Подчеркнем, что потенциальная энергия является характеристикой взаимодействия, по меньшей мере, двух тел. Нельзя говорить о том, что энергия взаимодействия «принадлежит» одному из тел, или каким образом «разделить эту энергию между телами». Поэтому, когда мы говорим об изменении потенциальной энергии, мы подразумеваем изменение энергии системы взаимодействующих тел. Однако в некоторых случаях допустимо все же говорить об изменении потенциальной энергии одного тела. Так, при описании движения небольшого, по сравнению с Землей, тела в поле тяжести Земли, говорим о силе действующей на тело со стороны Земли, как правило, не упоминая и не учитывая равную силу, действующую со стороны тела на Землю. Дело в том, что при громадной массе Земли, изменение ее скорости исчезающее мало. Поэтому изменение потенциальной энергии взаимодействия приводит к заметному изменению кинетической энергии тела и бесконечно малому изменению кинетической энергии Земли. В такой ситуации допустимо говорить о потенциальной энергии тела вблизи поверхности Земли, то есть всю энергию гравитационного взаимодействия «приписать» небольшому телу. В общем случае можно говорить о потенциальной энергии отдельного тела, если остальные взаимодействующие тела неподвижны.
Мы неоднократно подчеркивали, что точка, в которой потенциальная энергия принимается равной нулю, выбирается произвольно. В данном случае такой точкой оказалась бесконечно удаленная точка. В некотором смысле этот непривычный вывод, может быть признан разумным: действительно, на бесконечном расстоянии исчезает взаимодействие – исчезает и потенциальная энергия. С этой точки зрения логичным выглядит и знак потенциальной энергии. Действительно, чтобы разнести два притягивающиеся тела внешние силы должны совершить положительную работу, поэтому в таком процессе потенциальная энергия системы должна возрастать: вот она возрастает, возрастает и … становится равной нулю! Если притягивающиеся тела соприкасаются, то сила притяжения не может совершать положительную работу, если же тела разнесены, то такая работа может быть совершена при сближении тел. Поэтому часто говорят, о том, что притягивающиеся тела обладают отрицательной энергией, а энергия отталкивающихся тел положительна. Это утверждение справедливо, только в том случае, если нулевой уровень потенциальной энергии выбирается на бесконечности.
Так если два тела связаны пружиной, то при увеличении расстояния между телами, между ними будет действовать сила притяжения, тем не менее, энергия их взаимодействия является положительной. Не забывайте, что нулевому уровню потенциальной энергии соответствует состояние недеформированной пружины (а не бесконечность).
Примечания
- ↑ Вспомните, что сила гравитационного взаимодействия между сферически симметричными телами эквивалентна силе взаимодействия между точечными телами, таких же масс.