Слободянюк А.И. Физика 10/7.5
§7. Механика жидкости и газа
7.5 Основные законы гидростатики. Давление. Закон Паскаля. Закон Архимеда.
Наметив в самых общих чертах принципы кинематического описания движения жидкостей и газов, приступим к рассмотрению основных идей динамики движения, то есть выяснения причин, того или иного вида движения. Основным понятием динамики является взаимодействие тел и его характеристика – сила. Следовательно, для динамического описания движения жидкостей и газов необходимо рассмотреть взаимодействие различных частей жидкой среды между собой. Как мы уже отмечали, эти силы обусловлены межмолекулярными взаимодействиями, их полное описание чрезвычайно сложно, но сейчас нам нет необходимости досконально знать законы этих взаимодействий, достаточно принять во внимание, что при деформации жидкости (то есть изменении расстояния между молекулами) возникают силы упругости.
Помимо межмолекулярных сил (сил давления, обусловленных деформацией жидкости), на жидкость могут действовать и внешние силы, например, гравитационные (в частности, сила тяжести), инерционные, электрические, магнитные и т.д. Имеет смысл, разделить эти внешние силы на две группы – объемные, действующие, на все части жидкости, и поверхностные, действующие только на поверхность жидкости со стороны окружающих тел (например, стенок сосуда).
Пусть жидкость находится в состоянии покоя. В качестве исходных «аксиом» примем законы динамики Ньютона и очевидный экспериментальный факт - жидкость обладает свойством текучести. Полученные в данном разделе результаты в равной мере применимы и к газам.
Рассмотрим, какие следствия можно извлечь из этих «аксиом».
-
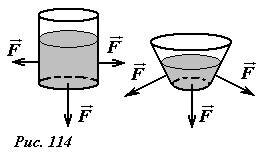
Сила, с которой покоящаяся жидкость действует на стенки сосуда, направлена перпендикулярно к этим стенке(рис. 114).
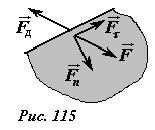
- Докажем это утверждение методом «от противного». В пусть в некоторой части сосуда, сила давления \(~\vec F_d\) , действующая на стенку, направлена под некоторым (не прямым) углом к последней. По третьему закону Ньютона, стенка действует на жидкость с силой \(~\vec F\), равной по величине и противоположной по направлению \(~\vec F = -\vec F_d\) . Разложим эту силу на нормальную (направленную перпендикулярно стенке) \(~\vec F_n\) и тангенциальную (направленную по касательной к стенке) \(~\vec F_{\tau}\) составляющие (рис. 115). При наличии тангенциальной силы, действующей на жидкость, жидкость, вследствие текучести, придет в движение. В состоянии равновесия таких сил быть не может. Следовательно, силы взаимодействия стенки и жидкости нормальны к стенке.
-
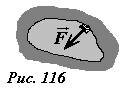
Силы, действующие на границу мысленно выделенного объема неподвижной жидкости, перпендикулярны этой границе (рис. 116).
- Это утверждение доказывается аналогично предыдущему, методом от противного.
- Итак, вопрос о направлении сил взаимодействия жидкости с сосудом и различных частей жидкости, решается однозначно – эти силы направлены по нормали к границе раздела. Если внутри жидкости выделить некоторую малую площадку, то модуль силы, действующей на одну сторону этой площадки, не зависит от ее ориентации. Это свойство внутренних сил позволяет ввести скалярную силовую характеристику взаимодействий внутри жидкости – давление.
- Строго говоря, силы взаимодействия между различными частями жидкости изменяются от точки к точке, поэтому изменение ориентации не малой площадки приведет к изменению силы, действующей на нее. Для малой [1] же площадки можно пренебречь изменением сил взаимодействия в ее пределах. Поэтому модуль рассматриваемой силы в этом случае оказывается пропорциональной площади. Следовательно, отношение модуля силы к площади площадки является характеристикой сил упругости внутри жидкости.
- Давление – отношение модуля силы, действующей на выделенную малую площадку, к площади этой площадки
-
\(~p = \frac{\Delta F}{\Delta S}\) , при ΔS → 0 . (1) - Как мы уже отмечали, жидкость может быть, как сжата, так и растянута, поэтому силы давления (силы упругости), оставаясь нормальными, могут быть направлены в разные стороны от границы жидкости. Для указания направления можно указывать знак давления. Принято считать давление положительным, если сила давления жидкости направлена наружу от рассматриваемого объема, что соответствует сжатой жидкости, в случае же растянутой жидкости силы упругости направлены внутрь жидкости, поэтому давление такой жидкости считается отрицательным.
- Понятно, что сила, действующая на площадку, может зависеть от ее положения внутри жидкости, поэтому и давление может изменяться при переходе от одной точке объема жидкости к другой. В этом смысле, давление следует рассматривать как точечную характеристику, то есть как функцию координат p(x,y,z).
- Конечно, измерить давление «в данной точке» измерить невозможно – измерению поддается только сила, действующая на площадку конечной площади. Кроме того, бессмысленно говорить о давлении на площадях, сравнимых с размерами отдельной молекулы. Однако с точки зрения простоты математического описания удобней рассматривать давление именно как функцию координат, понимая физическую ограниченность этого понятия.
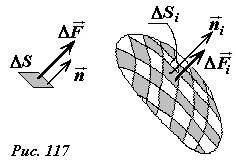
- Учитывая, что сила, действующая на малую площадку, направлена по нормали к площадке, а ее модуль выражается из формулы (1), вектор силы можно записать в виде \(~\Delta \vec F = p \Delta S \vec n\) , где \(~\vec n\) единичный вектор нормали к площадке. Для вычисления суммарной силы давления на некоторую поверхность внутри жидкости, необходимо разбить эту поверхность на малые участки (рис. 117), вычислить силу, действующую на каждую площадку, и просуммировать все эти силы \(~\vec F = \sum_{i} {p_i \Delta S_i \vec n_i}\) .
- Продолжим рассмотрение следствий из условий равновесия жидкости.
-
Векторная сумма внешних сил, действующих на любую мысленно выделенную часть неподвижной жидкости, равна нулю.
- Это утверждение просто повторяет общее условие равновесия любого тела, в том числе и жидкого.
-
При отсутствии объемных сил, действующих на жидкость, давление во всех точках объема одинаково.
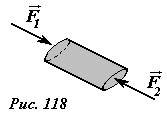
- Для доказательства этого положения, мысленно выделим внутри жидкости произвольно ориентированный узкий цилиндр (рис. 118). Так как жидкость в выделенном объеме находится в покое, то силы, действующие на основания цилиндра, равны по модулю и противоположны по направлению \(~\vec F_1 = -\vec F_2\) . Из этого соотношения и определения давления следует, что давления в точках оснований цилиндров равны. Аналогичные рассуждения справедливы для любого цилиндра, следовательно, давление во всех точках жидкости одинаково.
- Справедливо и обратное утверждение.
-
Если давление жидкости во всех точках одинаково, то суммарная сила, действующая на произвольную замкнутую поверхность, полностью находящуюся внутри жидкости, равна нулю.
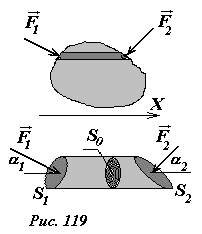
- Выделим внутри объема жидкости произвольную замкнутую поверхность. На каждый малый участок поверхности действует сила давления жидкости, направленная перпендикулярно данному участку. Докажем, что сумма проекций сил давления на произвольное направление (например, ось X) равна нулю. Для этого разобьем выделенную часть объема на узкие цилиндры, боковые поверхности которых параллельны выделенной оси (рис. 119). На основания этих цилиндров действуют силы давления, равные F1 = pS1, F2 = pS2, где S1, S2 - площади оснований цилиндров. Проекции сил на выбранное направление оси равны F1x = pS1cos α1, F2x = -pS2cos α2 , где α1, α2 - углы между нормалями к основаниям и осью X. Теперь заметим, что S1cos α1 = S2cos α2 = S0, где S0 - площадь поперечного сечения выбранного цилиндра, поэтому F1x + F2x = 0. Аналогичное соотношение справедливо для всех цилиндров, на которые разбито тело, поэтому сумма проекций сил на ось X равна нулю. Так как ось X выбрана произвольно, то сумма проекций сил давления на любую ось равна нулю, следовательно, и векторная сумма рассматриваемых сил также равна нулю.
-
(Закон Паскаля). Давление на поверхность жидкости, произведенное внешними силами, передается жидкостью во все стороны одинаково.
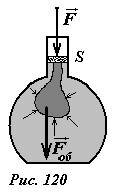
- Данный закон справедлив и в том случае, когда на жидкость действуют объемные силы. Пусть жидкость находится в сосуде под поршнем (рис. 120). Приложим к поршню дополнительную нормальную силу \(~\vec F\) . Под действием этой силы жидкость дополнительно сожмется, что приведет к увеличению давления. В состоянии равновесия эта дополнительная сила будет скомпенсирована равным увеличением силы давления на поршень со стороны жидкости. Следовательно, увеличение давления жидкости непосредственно под поршнем будет равно \(~\Delta p_0 = \frac{F}{S_0}\) , где S0 - площадь поршня. Выделим внутри жидкости произвольную замкнутую поверхность, часть которой совпадает с поверхностью поршня. В состоянии равновесия сумма объемных сил \(~\vec F_{ob}\), действующих на выделенную часть жидкости, и поверхностных сил давления \(~\vec F_{pov} = \sum_{i} {p_i \Delta S_i \vec n_i}\) равна нулю:
-
\(~\vec F_{ob} + \sum_{i} {p_i \Delta S_i \vec n_i} = \vec 0\) . (2) - Дополнительная сила давления на часть выбранной поверхности под поршнем должна быть скомпенсирована увеличением поверхностных сил давления на остальную поверхность. Обозначим увеличение давления вблизи части ΔSi поверхности - Δpi . В состоянии равновесия должно выполняться соотношение, аналогичное (2)
-
\(~\vec F_{ob} + \sum_{i} {(p_i + \Delta p_i) \Delta S_i \vec n_i} = \vec 0\) . (3) - Учитывая, что суммарная объемная сила не изменилась, из (2), (3) следует, что соотношение
-
\(~\sum_{i} {\Delta p_i \Delta S_i \vec n_i} = \vec 0\) , - должно выполняться для любой поверхности внутри объема жидкости, что возможно только в том случае, если величины Δpi одинаковы во всех точках жидкости, то есть \(~\Delta p_i = \Delta p_0 = \frac{F}{S_0}\) . Отметим, что закон Паскаля можно интерпретировать следующим образом: в состоянии равновесия изменение давления в одной точке жидкости приводит к равному изменению давления во всех остальных точках жидкости.
- Существенным в данной формулировке является упоминание о состоянии равновесия, потому, что при увеличении давления в некоторой точке жидкости, требуется некоторый промежуток времени, чтобы произошло установления равновесия в остальных частях объема жидкости, иными словами, возмущение жидкости распространяется внутри объема с конечной скоростью. Позднее мы покажем, что эта скорость есть скорость распространения упругих волн (т.е. звука) в данной жидкости.
- Важными следствием закона Паскаля является, так называемый, «гидростатический парадокс» - давление жидкости на дно сосуда не зависит от формы сосуда, который проявляется в свойствах сообщающихся сосудов. Закон Паскаля также является теоретическим обоснованием таких устройств как гидравлический пресс, сифон и т.д.
-
В поле тяжести земли давление жидкости на глубине h определяется по формуле
-
\(~p = \rho g h\) , (4) - где ρ - плотность жидкости, g - ускорение свободного падения. Давление, определяемое формулой (4), называется гидростатическим.
- Для вывода этой формулы достаточно выделить внутри объема жидкости вертикальный цилиндр высотой h, верхнее основание которого площадью S находится на свободной поверхности жидкости, и рассмотреть условия его равновесия. Объемные силы, действующие на жидкость внутри выделенного цилиндра (в данном случае это сила тяжести mg = ρgV = ρghS) уравновешивается силой давления на нижнее основание цилиндра ρS. Из условия равенства этих сил следует формула (4).
- Заметим, что формула (4) описывает только ту часть давления, которая обусловлена силой тяжести, действующей на жидкость. В общем случае полное давление на глубине h будет равно сумме гидростатического давления и внешнего давления на поверхность жидкости (например, атмосферного давления).
-
-
(Закон Архимеда). На погруженное в жидкость тело, действует выталкивающая сила, равная суммарной объемной силе, действующей на жидкость в объеме тела.
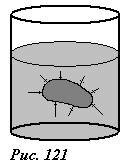
- Доказательство этого закона достаточно просто. По своей природе выталкивающая сила есть векторная сумма сил давления жидкости на поверхность тела (рис.121). Следовательно, эта сила определяется распределением давления жидкости вблизи поверхности тела. Мысленно уберем тело из жидкости, оставив только его «оболочку», которую заполним той же жидкостью. От такой замены суммарная сила давления на поверхность не изменится. С другой стороны, очевидно, что жидкость в объеме тела, находящаяся в такой же жидкости будет находиться в равновесии. Поэтому суммарная сила давления будет равна по величине и противоположна по направлению объемной силе, действующей на жидкость в объеме тела.
- В частном случае, если единственной объемной силой является сила тяжести, и при постоянной плотности жидкости ρ, выталкивающая сила (сила Архимеда FA) по модулю равна силе тяжести, действующей на жидкость в объеме тела V и противоположна ей по направлению:
-
\(~F_A = \rho g V\) , или в векторной форме \(~\vec F_A = -\rho \vec g V\) . - Заметим, что выталкивающая сила появляется только в том случае, когда давление внутри жидкости различно в различных точках. В случае постоянного давления (каким бы большим оно не было) суммарная сила давления равна нулю. Различие давлений обусловлено только объемными силами, действующими на жидкость. Поверхностные силы, как было нами показано, не могут привести к возникновению разности давлений в различных точках жидкости. Допустим, что жидкость находится под поршнем – увеличения силы давления на поршень не приведет к увеличению выталкивающей силы, действующей на погруженное в жидкость тело.
- В общем случае выталкивающая сила может описываться более сложными формулами, которые могут учитывать изменение плотности жидкости, изменение ускорения свободного падения, как по величине, так и по направлению, присутствие других объемных сил – инерционных, электрических, магнитных и т.д.
Примечания
- ↑ Точнее следует говорить о бесконечно малой площадке.