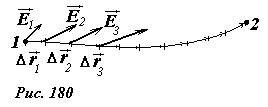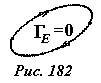Слободянюк А.И. Физика 10/9.10

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.10 Связь между потенциалом и напряженностью электрического поля.

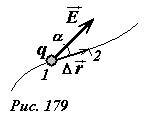
Потенциал является важной характеристикой электрического поля, он определяет всевозможные энергетические характеристики процессов, проходящих в электрическом поле. Кроме того, расчет потенциала поля проще расчета напряженности, хотя бы потому, что является скалярной (а не векторной) величиной. Безусловно, что потенциал и напряженность поля связаны меду собой, сейчас мы установим эту связь. Пусть в произвольном электростатическом поле точечный заряд q совершил малое перемещение \(~\Delta \vec r\) из точки 1 в точку 2 (Рис. 179). Пренебрегая изменением напряженности поля \(~\vec E\) на этом участке, работу, совершенную полем можно записать в виде

\(~\delta A = \vec F \cdot \Delta \vec r = q \vec E \cdot \Delta \vec r\) .

По определению эта величина равна разности потенциалов, взятой с противоположным знаком, деленной на величину заряда, поэтому

\(~\Delta \varphi = \varphi_2 - \varphi_1 = -\frac{\delta A}{q} = - \vec E \cdot \Delta \vec r\) . (1)

Если расстояние между точками 1 и 2 не является малым, то необходимо эти точки соединить произвольной линией (Рис. 180), разбить ее на малые участки \(~\Delta \vec r_1, \Delta \vec r_2, \Delta \vec r_3, \ldots\) и просуммировать разности потенциалов между (1) ними

\(~\varphi_1 - \varphi_2 = \vec E_1 \cdot \Delta \vec r_1 + \vec E_2 \cdot \Delta \vec r_2 + \vec E_3 \cdot \Delta \vec r_3 + \ldots\) . (2)

Формула (2) позволяет рассчитать разность потенциалов между произвольными точками, по известным значениям напряженности поля во всех точках.

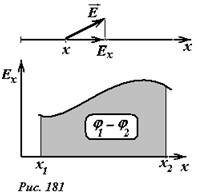
Как и следовало ожидать, связь между разностью потенциалов и напряженностью поля аналогична связи между изменением потенциальной энергии и действующей силой. Так, если вдоль некоторой прямой (назовем ее осью X), проекция вектора напряженности на эту ось изменяется по некоторому закону E_X(x), то площадь под графиком этой функции между точками с координатами x₁ и x₂ численно равна разности потенциалов между этими точками, взятой с противоположным знаком.

Заметим, что если двигаться вдоль направления вектора напряженности, то потенциал поля будет уменьшаться, так как при таком движении поле совершает положительную работу, поэтому энергия взаимодействия уменьшается.

Так как электростатическое поле является потенциальным, то результат суммирования в формуле (2) не зависит от выбранной линии, важно только, чтобы она начиналась в точке 1 и заканчивалась в точке 2. Кстати, с подобной конструкцией сумма скалярных произведений вектора на малый элемент траектории мы уже неоднократно встречались. Напомним, что такая сумма, вычисленная по замкнутой траектории, называется циркуляцией векторного поля.

Так как электростатическое поле потенциально, то циркуляция вектора напряженности электростатического поля по любой замкнутой линии равна нулю Г_E = 0(Рис. 182).

Таким образом, мы сформулировали вторую важнейшую теорему для вектора напряженности стационарного электростатического поля. Никакого нового физического содержания в этой теореме нет – это просто повторение в иной форме свойства потенциальности. Заметим также, что теорема о циркуляции утверждает, что в электростатическом поле не может быть замкнутых силовых линий, все силовые линии начинаются и заканчиваются на электрических зарядах, или что равносильно – единственными источниками электростатического поля являются электрические заряды. Заметим, что данной утверждении справедливо, только в статических полях (не зависящих от времени), в дальнейшем мы познакомимся с электрическим полями, в которых существуют замкнутые силовые линии, такие поля порождаются изменяющимися магнитными полями.

Задание для самостоятельной работы.

1. Докажите, что в электростатическом поле не могут существовать замкнутые силовые линии.

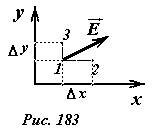
Формула (1) позволяет выразить значение вектора напряженности через известное распределение потенциала поля. Только не следует делить на вектор – такая операция в математике еще не определена. Рассмотрим две близких точки 1 и 2, находящиеся на прямой, параллельной оси X на малом расстоянии Δx (Рис. 183). Пусть напряженность вблизи этих точек равна \(~\vec E\) , и ее изменением пренебрежем из-за близости рассматриваемых точек. Тогда разность потенциалов между этими точками равна

\(~-\Delta \varphi = \varphi_1 - \varphi_2 = \vec E \cdot \Delta \vec r = E_x \cdot \Delta x\) .

Из этого выражения законно находим проекцию вектора напряженности на ось X:

\(~E_x = -\frac{\Delta \varphi}{\Delta x} = -\frac{\varphi(x + \Delta x,y,z) - \varphi(x,y,z)}{\Delta x}\) . (3)

Аналогично, рассматривая две близких точки 1 и 3, находящиеся на прямой, параллельной оси Y на малом расстоянии Δy, можно получить выражение для проекции вектора напряженности на ось Y:

\(~E_y = -\frac{\Delta \varphi}{\Delta y} = -\frac{\varphi(x,y + \Delta y,z) - \varphi(x,y,z)}{\Delta y}\) . (4)

Выражение для проекции вектора на ось Z - E_z также полностью аналогично

\(~E_z = -\frac{\Delta \varphi}{\Delta z} = -\frac{\varphi(x,y,z + \Delta z) - \varphi(x,y,z)}{\Delta z}\) . (5)

Особо отметим, что величины Δφ, фигурирующие в формулах (3)-(5) различны, так как они выражают разности потенциалов между близкими точками, но смещенными в различных направлениях.

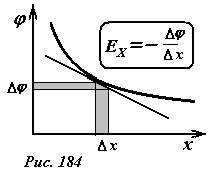
Полученным выражениям для напряженности поля можно дать и графическую интерпретацию (Рис. 184): коэффициент наклона касательной к графику зависимости φ(x), взятый с обратным знаком, численно равен проекции вектора напряженности на ось X.

В общем случае потенциал электрического поля зависит от трех координат точки, поэтому графически представить эту зависимость невозможно. Мы уже пользовались зависимостью потенциала от одной координаты φ(x) и строили графики этой зависимости. Фактически, мы задавали зависимость потенциала от одной координаты, при движении вдоль прямой параллельной оси x, если мы выберем другую прямую, также параллельную оси x, то получим другую функцию φ(x). Поэтому при рассмотрении подобных зависимостей надо явно указывать на какой прямой, рассматривается потенциал. Проще всего, во избежание путаницы указывать в явном виде при каких значениях других координат y₀ = const, z₀ = const рассматривается зависимость φ(x) = φ(x,y₀,z₀). Точно также можно изучать зависимость потенциала от двух координат, считая третью постоянной: например, φ(x,y) = φ(x,y,z₀) . То есть, рассматривать распределение потенциала в некоторой плоскости параллельной координатной плоскости xOy, находящей на расстоянии z₀ от нее. Графически эта зависимость может быть представлена некоторой поверхностью, высота точек которой пропорциональна потенциалу в данной точке, такую поверхность далее будем называть потенциальной, по аналогии с потенциальными кривыми, рассмотренными нами ранее. Так на рисунке в качестве примера показана потенциальная поверхность поля точечного заряда, в плоскости, содержащей заряд этот заряд.

Если точечный заряд q находится в начале некоторой системы координат, то потенциал поля, создаваемого этим зарядом в произвольной точке с координатами (x,y,z) определяется формулой

\(~\varphi(x,y,z) = \frac{q}{4 \pi \varepsilon_0 r} = \frac{q}{4 \pi \varepsilon_0 \sqrt{x^2 + y^2 + z^2}}\) . (6)

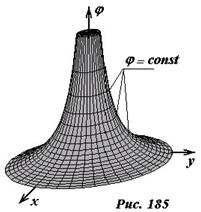
Если мы хотим построить распределение потенциала в плоскости xOy, то в формуле (6) следует положить z = 0. Поверхность, описываемая этим уравнением, показана на рисунке 185. Заметим, что в начале координат потенциал стремится к бесконечности, поэтому изображение потенциальной поверхности искусственно обрезан сверху.

Потенциальные поверхности строить не легко, для этого, как правило, используется компьютер. Однако изображения таких поверхностей бывают очень полезными при анализе движения заряженных частиц. Так движение положительно заряженной частицы в поле, описываемом заданной потенциальной поверхностью, аналогично движению массивного шарика в поле тяжести земли по геометрической поверхности, которая совпадает с потенциальной.

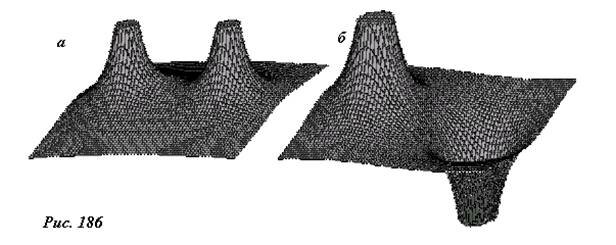
На рисунке 186 для примера построены потенциальные поверхности поля, создаваемого двумя одинаковыми по модулю зарядами: а) одинаковых знаков; б) противоположных знаков.

Вторым способом графического представление потенциала является построение эквипотенциальных поверхностей, то есть геометрического места точек, имеющих одинаковый потенциал, то есть удовлетворяющих уравнению φ(x,y,z) = φ₀ = const.

Так для поля точечного заряда (1) эквипотенциальными поверхностями являются сферы, концентрические с точечным зарядом – все точки, находящиеся на одинаковом расстоянии от заряда, имеют одинаковый потенциал. Формально, уравнение эквипотенциальной сферы можно получить из функции (6). Из уравнения

\(~\frac{q}{4 \pi \varepsilon_0 \sqrt{x^2 + y^2 + z^2}} = \varphi_0\) . (6)

следует уравнение сферы \(~x^2 + y^2 + z^2 = \left (\frac{q}{4 \pi \varepsilon_0 \varphi_0} \right )^2\) , причем сфера большего потенциала имеет меньший радиус.

Заметим, что симметрия эквипотенциальных поверхностей повторяет симметрию источников поля, так поле точечного заряда сферически симметрично, то и эквипотенциальные поверхности обязаны быть сферами.

Конечно, для увеличения наглядности, следует рассматривать не одну эквипотенциальную поверхность, а их семейство. Однако изобразить графически семейство сложных поверхностей на одном рисунке крайне затруднительно. Поэтому часто графически изображают только сечения эквипотенциальных поверхностей некоторой плоскостью, или, что равносильно – множества точек равного потенциала в некоторой плоскости (которые являются линиями).

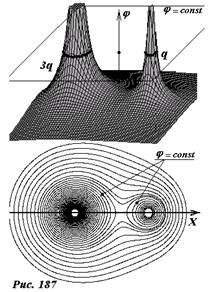
Линии равного потенциала и потенциальные поверхности тесно связаны между собой. Фактически линии равного потенциала является сечениями потенциальной поверхности. Семейство эквипотенциальных линий полностью аналогично линиям равной высоты (изолиниям) на географической карте. На рисунке 187 показана потенциальная поверхность электростатического поля, созданного двумя точечными зарядами одного знака, но разной величины, в плоскости, содержащей эти заряды. Ниже построено семейство эквипотенциальных линий этого поля в той же плоскости. Эти линии являются линиями уровня для потенциальной поверхности.

В данном примере легко вообразить и семейство трехмерных эквипотенциальных поверхностей. Система двух точечных зарядов обладает осевой симметрией – осью симметрии является прямая, проходящая через оба заряда, на рисунке она обозначена как ось X. Поэтому и поле, и его эквипотенциальные поверхности обладают осевой симметрией – достаточно повернуть картину эквипотенциальных линий вокруг оси X, чтобы получить семейство эквипотенциальных поверхностей.

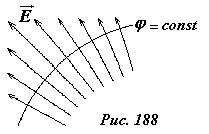
Эквипотенциальные поверхности также тесно связаны с силовыми линиями электрического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, так работа по перемещению заряда q пропорциональна изменению потенциала \(~\delta A = -q \Delta \varphi\) , а на эквипотенциальной поверхности Δφ = 0. С другой стороны эта работа выражается через напряженность поля \(~\vec E\) как \(~\delta A = q \vec E \cdot \Delta \vec r = q E \Delta r \cos \alpha\) (где \(~\Delta \vec r\) - вектор перемещения заряда, α - угол между векторами напряженности поля и перемещения). Если вектор перемещения направлен вдоль эквипотенциальной поверхности, то работа поля равна нулю, следовательно, вектор напряженности в этом случае перпендикулярен вектору перемещения (косинус прямого угла равен нулю). Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (Рис. 188). Если же вектор перемещения направлен вдоль силовой линии, то изменение потенциала будет максимальным, следовательно, силовые линии указывает направления максимального изменения (точнее уменьшения) потенциала.

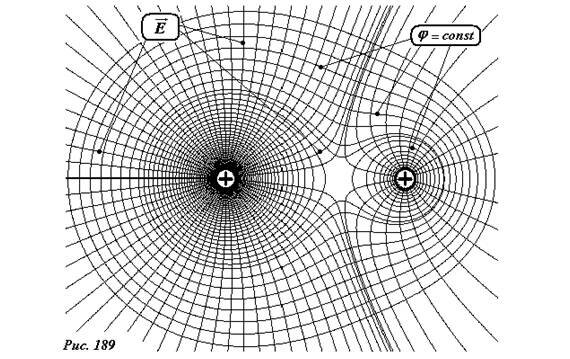
На рисунке 189 показаны одновременно семейства силовых линий и семейство эквипотенциальных поверхностей поля двух точечных зарядов, рассмотренных ранее.

Следующая страница