A. Интерференция света
Интерференция света в тонких пленках
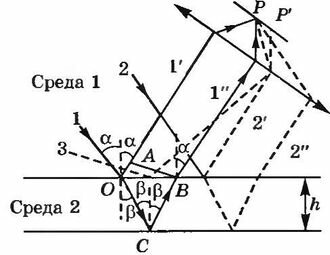
Наблюдаемое в природе радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах) объясняется интерференцией света, возникающей в результате отражения света от передней и задней поверхностей пленки. На рисунке 17.9 изображена тонкая плоскопараллельная прозрачная пленка, на которую падают лучи света. В точке О свет частично отразится от верхней поверхности пленки (волна \(~1'\)), а частично преломится и отразится от задней ее поверхности в точке С и, преломившись в точке В, выйдет в воздух параллельно волне \(~1'\). Волны \(~1'\) и \(~1''\) когерентны.
Если на пути этих лучей поставить собирающую линзу, то они будут накладываться в ее фокальной плоскости и давать интерференционную картину, которая определяется их оптической разностью хода \(\Delta = n_2(OC+CB)-n_1 \cdot OA \pm \frac{\lambda}{2}\) где член \(\frac{\lambda}{2}\) — обусловлен потерей полуволны при отражении света от границы раздела оптически более плотной среды. Если \(~n_2 > n_1 ,\) то потеря полуволны произойдет в точке О, и этот член будет со знаком "плюс"\[\Delta = n_2(OC + CB) - n_1 \Bigr(OA - \frac{\lambda}{2} \Bigl).\] Если \(~n_2 < n_1,\) то потеря полуволны произойдет в точке С, и он будет иметь знак "минус"\[\Delta = n_2 \Bigr(OC + CB- \frac{\lambda}{2} \Bigl) - n_1 OA .\]
Пусть тонкая пленка находится в воздухе (n1 = 1). Из рисунка 17.9 видим, что \(~OA = OB \sin \alpha ;\) \(~OB = 2htg \beta;\) \(OC = CB = \frac{h}{\cos \beta},\) где \(~\alpha\) и \(~\beta\) — углы падения и преломления соответственно. Тогда физическая разность хода \(\Delta = \frac{2hn_2}{\cos \beta} - 2htg \beta \sin \alpha + \frac{\lambda}{2}.\) Из закона преломления найдем, что \(\sin \beta = \frac{\sin \alpha}{n_2}.\) Учтем, что \( \cos \beta = \sqrt{1 - \sin^2 \beta},\) а \( tg \beta = \frac{sin \beta}{\sqrt{1 - \sin^2 \beta}}.\) После несложных математических преобразований получим:
1. Полосы равного наклона.
Как видно из последней формулы, интерференционная картина определяется значениями длины волны \(\lambda\), толщины пластинки h, показателя преломления n и угла падения \(~\alpha\). Для данных \(\lambda\), n и h каждому наклону соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пленку под одинаковыми углами, называются полосами равного наклона.
Лучи 3, наклоненные под другим углом, соберутся в другой точке \(P'.\) Если оптическая ось линзы перпендикулярна поверхности пластинки, полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
2. Полосы равной толщины.
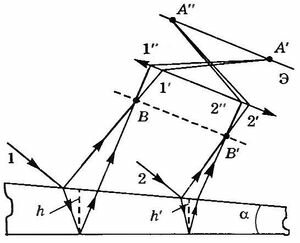
На рисунке 17.10 изображена клиновидная пластинка (угол \(~\alpha\) между боковыми гранями мал). На нее падает свет, направление распространения которого совпадает с параллельными лучами \(~1\) и \(~2.\)
Когерентные лучи \(~1'\) и \(~1''\) дают интерференционную картину в точке А', которая определяется разностью хода этих лучей и будет зависеть от толщины h клина в месте падения на него луча. Лучи \(~2'\) и \(~2''\) собираются линзой в точке \(А''.\) Оптическая разность хода определяется толщиной h' . Таким образом, на экране наблюдаются интерференционные полосы. Каждая из полос возникает за счет отражения от мест пластинки, имеющих одинаковую толщину.
Интерференционные полосы на поверхности пленки имеют одинаковую освещенность на всех точках поверхности, соответствующих одинаковым толщинам пленки, и называются полосами равной толщины.
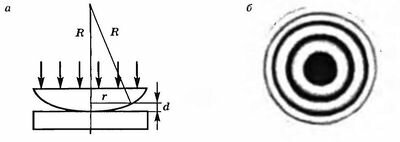
Примером полос равной толщины являются кольца Ньютона, которые наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 17.11, а). Воздушная прослойка постепенно утолщается от точки соприкосновения линзы к краям. Отраженные от верхней и нижней границ воздушной прослойки световые волны интерферируют между собой. При этом получается следующая картина: в точке соприкосновения наблюдается черное пятно, окруженное рядом концентрических световых и черных колец убывающей ширины (рис. 17.11, б).
Как для полос равного наклона, так и для полос равной толщины, положения максимумов зависят от \(\lambda.\) Поэтому при освещении монохроматическим светом получается система темных и ярких полос, а при наблюдении в белом свете интерференционная картина приобретает радужную окраску. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не происходит потери полуволны. В результате максимумы интерференции в отраженном свете соответствуют минимумам в проходящем и наоборот.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 508-510.