Kvant. Аристотель
Мякишев Г. Если бы Аристотель был прав //Квант. — 1995. — № 2. — С. 18-21.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Содержание
- 1 Классификация движений
- 2 Трудности в механике Аристотеля
- 3 Гелиоцентрическая модель Вселенной
- 4 Множественность миров
- 5 Зарождение новой (теперь ее называют классической) механики
- 6 Суть механики Ньютона
- 7 Когда Аристотель прав?
- 8 Когда Аристотель неправ?
- 9 Не существовало бы планетных систем
- 10 Механика Аристотеля и антропный принцип
- 11 Примечания
Классификация движений
Великий Аристотель (384 - 322 до н.э.) с самого начала, казалось бы, поступил совершенно правильно: чтобы разобраться в многообразии видимых движений, нужно их рассортировать — классифицировать.
В те далекие времена Земля считалась центром Вселенной, и все движения рассматривались, естественно, по отношению к Земле. Идее относительности движения не было места.
Естественные движения
В первую очередь следует выделить естественные движения тел, которые называются так потому, что их не надо поддерживать извне. Они совершаются по раз и навсегда заведенному порядку и определяются природой тел.
Тяжелые предметы падают на Землю сами собой, стремясь к центру Вселенной, а легкие тела, подобные огню, поднимаются вверх, так как стремятся к своему естественному месту — краю области, окружающей центр Вселенной (рис. 1).
Другой вид естественного движения — это движение звезд, Солнца, Луны и планет (рис. 2). Они совершают равномерное круговое движение относительно центра мироздания, ибо именно такое движение является наиболее простым и совершенным. Тела эти состоят из особой небесной субстанции и потому не падают на Землю.
Принудительные движения
Наряду с естественными движениями существуют принудительные. Это те движения, которые не могут происходить сами собой и побуждаются внешними воздействиями — силами. Например, для движения повозки ее все время должна тянуть лошадь (рис. 3). И чем сильнее она тянет, тем быстрее движется повозка. Ее скорость прямо пропорциональна силе. Повозка сразу же останавливается после прекращения внешнего воздействия.
Трудности в механике Аристотеля
Представления Аристотеля, по словам выдающегося современного американского философа и историка науки Томаса Куна[1], «не лишены смысла». Более того, Кун считает, что физика Аристотеля «не просто плохая физика Ньютона; она совсем другая».
В самом деле, ведь Аристотель четко фиксирует то, что каждый из нас видит каждый день (или каждую ночь): Солнце, Луна и звезды движутся по окружностям, камни падают вниз, а любая повозка остановится, если ее перестанут тянуть или толкать. Однако немало движений не совсем укладываются в классификацию Аристотеля и для их «объяснения» приходится прибегать к различным ухищрениям.
Природа не терпит пустоты
Можно проделать очень простой опыт. Нарисуем на полу небольшой круг. Проходя с мячом в руке рядом с ним, нужно на ходу разжать пальцы так, чтобы мяч попал в круг. Если выпустить мяч точно над кругом, то он в него не попадет. Мяч почему-то летит не просто вниз, но еще и вперед по ходу движения. (Как выявили исследования, проведенные в колледжах США, далеко не каждый школьник сразу понимает, что мяч надо выпускать не над кругом, а заранее.)
Как же объясняет падение мяча Аристотель? Вначале мяч движется принудительно под действием руки. При этом за мячом возникают завихрения воздуха, которые и толкают его вперед после того, как пальцы разжались. Здесь складываются естественное движение (падение вниз) и принудительное под действием завихрений воздуха (движение вперед).
А что будет, если мяч бросить в пустоте? Ответ Аристотеля гениально прост: этого вы сделать не можете, так как природа не терпит пустоты.
Блуждающие звезды
Почему Аристотель и его современники были убеждены в том, что именно Земля — центр Вселенной? Это же совершенно «очевидно» I Вокруг чего иного, как не центра мироздания, могут совершать звезды свои идеальные пути? К чему, как не к центру, стремятся падающие тела?
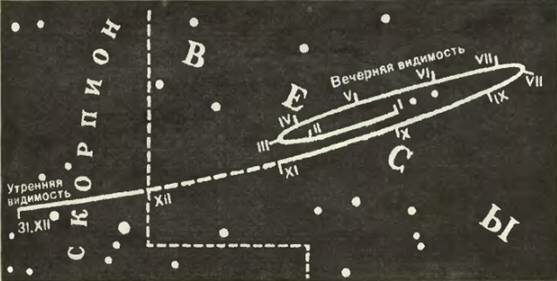
Однако давно уже было подмечено, что движение не всех небесных тел такое уж идеальное. Планеты — «блуждающие звезды», как их называли, — описывают на небе какие-то замысловатые петли (рис. 4). Аристотель мог этого и не знать, но когда тщательные наблюдения астрономов установили это бесспорно, здание механики Аристотеля зашаталось. Зашаталось, но не рухнуло. Клавдий Птолемей (ок. 100 — ок. 165) объяснил загадочные движения планет, не отказываясь от идеи Аристотеля о совершенном равномерном движении небесной субстанции по окружностям.
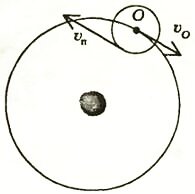
Каждая планета движется вокруг некоторого центра О (рис. 5), а сам этот центр обращается по окружности вокруг Земли. В момент, когда скорость \(~\vec \upsilon_O\) точки О противоположна скорости планеты \(~\vec \upsilon_p\), земному наблюдателю кажется, что планета поворачивает назад.
Сложная и несколько запутанная система мира Птолемея тем не менее позволяла предсказывать положения планет довольно точно.
Гелиоцентрическая модель Вселенной
Великий шаг в понимании природы был сделан польским ученым Николаем Коперником (1473 - 1543).
В центре мироздания он вместо Земли поместил Солнце. Благодаря этому сложные движения планет оказались очень простыми, если принять, что все планеты, и Земля в том числе, обращаются вокруг Солнца.
Однако создание системы Коперника не так уж много изменило в механике Аристотеля. Просто место Земли заняло Солнце. Объяснение видимого движения звезд вращением Земли внесло идею относительности движения, но подтверждало мысль Аристотеля о том, что движение по окружности — это естественное движение.
Множественность миров
Истинный переворот в понимании механического движения связан с именем итальянского мыслителя Джордано Бруно (1548—1600). Бруно выдвинул идею множественности миров. Солнце не является центром мироздания; оно — одна из бесчисленных звезд, но только расположено недалеко от нас[2]. Это и нанесло решающий удар по механике Аристотеля. Если нет центра мироздания, то бессмысленно говорить о естественном движении вокруг него, и вся классификация движений как отправной метод построения механики утрачивает опору. Поэтому Бруно не только великий астроном, но и великий механик. Фактически его идею следует понимать как принцип равноправности всех мест Вселенной.
Разрушив основную идею механики Аристотеля, Бруно ничего нового на ее месте не сумел создать. Он был обвинен инквизицией в ереси и 17 февраля 1600 года сожжен на костре.
Зарождение новой (теперь ее называют классической) механики
Галилео Галилей (1564 - 1642) первым совершенно отчетливо понял, что отсутствие центра Вселенной не позволяет говорить о движении как о чем-то абсолютном (относительно Земли у Аристотеля или относительно Солнца у Коперника). Движение относительно: можно с полным основанием говорить о движении любого тела по отношению к любому другому. Ну а если движения относительны, ясно, что их классификация — занятие довольно бесперспективное. Так, для человека, отдыхающего в парке на скамейке, и для другого, который в это время катается на карусели, все вокруг движется по-разному.
Не ведет ли это к хаосу, если нельзя даже классифицировать движения? Полностью от классификации движений Галилей не отказался. Но подход к классификации у него был принципиально иным, чем у Аристотеля. Отказавшись вслед за Дж. Бурно от представлений о центре Вселенной, Галилей с неизбежностью пришел к мысли, что если и существует «естественное» движение, то это движение тел, которые движутся «сами по себе», не подвергаясь никаким воздействиям. По мнению Галилея, естественное движение, или движение по инерции, — это прямолинейное движение с постоянной скоростью. В какой-то мере это кажется очевидным: ведь если тело не испытывает воздействия, то оно движется как бы в пустоте. Движение в пустом пространстве нигде не может ни ускориться, ни замедлиться. Тело не может повернуть ни налево, ни направо — просто для таких изменений движения не видно никаких причин.
Однако ни с чем не взаимодействующих тел нет и быть не может. Откуда же у Галилея возникла уверенность в справедливости его умозрительных доводов? Галилей отчетливо понял, что естественному движению с постоянной скоростью мешает сопротивление окружающей среды (воздуха, воды) или сила трения со стороны твердых поверхностей, по которым происходит движение. Простые опыты прямо указывают, что чем меньше сопротивление или трение, тем менее заметно изменяется скорость и тем дольше продолжается движение.
Здесь надо подчеркнуть еще один принципиально важный момент. Огромная, даже основная заслуга Галилея в том, что он по-новому понял, что такое законы движения. Ведь как было у Аристотеля: вижу — классифицирую; классификация движений — непосредственное обобщение наблюдений. У Галилея другой подход: он за видимыми движениями искал потаенную, сокровенную суть управляющих ими законов. Путь Галилея привел к возможности установить общие законы механического движения. Но для этого потребовался гений Ньютона.
Суть механики Ньютона
Есть нечто символическое в том, что Исаак Ньютон (1643 - 1727) родился почти точно через год после того, как не стало Галилея, и в том, что младенец, родившийся крохотным и совсем слабеньким (по словам современника, его можно было утопить в пивной кружке), вошел в историю как один из величайших титанов человеческого духа.
Ньютон понял и математически сформулировал основной факт, относящийся к механическому движению: воздействия тел друг на друга (силы) во всех без исключения случаях определяют не скорости движения тел, как считал Аристотель, а ускорения, т.е. быстроту изменения скорости[3]. В этом и состоит то, что мы называем инерцией. Ускорение возникает сразу, одновременно с началом действия силы, а скорость нарастает постепенно. Даже очень большая сила не в состоянии сообщить телу сразу значительную скорость. Для этого нужно время. Чтобы остановить тело, опять-таки нужно, чтобы тормозящая сила (трение, сопротивление среды или что-либо иное) действовала некоторое время.
Силы — причины изменения состояния движения тел, т.е. их скорости. И если что и нужно классифицировать в первую очередь, то это типы сил, а не типы движений, которые зависят от системы отсчета.
Ньютон сформулировал основной закон динамики (второй закон), который называют уравнением движения: произведение массы на ускорение равно сумме всех действующих на тело сил:
Когда Аристотель прав?
А теперь попробуем перевести качественные представления Аристотеля о движении тел на математический язык, используя понятия и величины, входящие в механику Ньютона.
С самого начала надо отвергнуть разделение движений на естественные и принудительные. С точки зрения механики Ньютона, все движения надо отнести к принудительным (исключая движения свободных тел). Законы механики универсальны, и никакой «небесной субстанции» не существует. Поэтому движения небесных тел — планет, Луны и звезд — должны подчиняться тем же законам, что и падение камня на Землю, и движение повозки, влекомой лошадью. Мы теперь знаем, что в рамках применимости, когда можно пренебречь релятивистскими и квантовыми эффектами, механика Ньютона совершенно справедлива.
Движение, по Аристотелю, безынерционно, т.е. никакого времени для приобретения скорости не требуется, а скорость однозначно определяется приложенной силой. В каких случаях это предположение приблизительно справедливо?
Очевидно, в тех случаях, когда произведение массы на ускорение во втором законе Ньютона много меньше всех сил, действующих на тело, в том числе и силы сопротивления (трения):
Значит, механика Аристотеля вполне применима для установившегося движения, когда скорость не меняется и ускорение равно нулю (или очень мало). Это довольно распространенные случаи. Вот почему даже в наше время можно встретить людей, которые смотрят на движение так же, как Аристотель, впрочем, не отдавая себе в этом отчета.
Установившееся движение описывается уравнением
где \(~\vec F_c\) — сила сопротивления, зависящая от скорости. Видно, что величина силы сопротивления, а значит, и величина скорости однозначно определяются силой \(~\vec F\). Так, если предположить, что \(~\vec F_c = - \mu \vec \upsilon\), то получим
По Аристотелю, скорость тела тем меньше, чем больше сопротивление среды. Если же сопротивления нет совсем, то под действием силы тело сразу же приобретает бесконечную скорость. Так, в пустоте, по словам Аристотеля, тело падало бы с бесконечно большой скоростью. Этого не происходит только потому, что природа не терпит пустоты.
Уравнение (2) можно назвать «вторым законом» в механике Аристотеля. Как мы увидим дальше, оно совершенно не годится для описания переходных процессов, предшествующих установившемуся движению. Однако чем меньше масса и чем больше коэффициент сопротивления μ, тем меньше интервал времени, на котором механика Аристотеля несостоятельна.
Третий закон можно считать выполняющимся в обеих механиках, хотя сам Аристотель на этот счет ничего не говорит.
Первый закон претерпевает неизбежные существенные изменения. В механике Аристотеля свободное тело, т.е. тело, на которое не действуют силы, будет находиться в покое. Роль инерциальной системы ньютоновской механики будет играть система отсчета, в которой свободное тело покоится. Принцип относительности не выполняется.
Когда Аристотель неправ?
С самого начала здесь нужна оговорка. Ведь если бы Аристотель в самом деле был во всем прав и существовала бы небесная субстанция, из которой состоят тела, движущиеся относительно Земли по совершенным круговым орбитам, то такой мир мог бы существовать и в нем была бы возможна жизнь. Наше заявление в начале статьи в этом отношении двусмысленно. (Неслучайно Кун говорит не о ложности механики Аристотеля, а лишь об отличии ее от механики Ньютона.) Но все же, если признать в принципе возможным научный подход к теории принудительных движений по Аристотелю и признать все движения принудительными, то в этом и только в этом смысле можно сказать, что жизнь в мире, подчиненном механике Аристотеля, невозможна. «Объяснения» же Аристотелем естественных движений и выделение их в основной тип движений ни в каком отношении научным считать нельзя. Все сводится здесь к утверждению: «тела движутся так, а не иначе, потому что мы видим, что они именно так движутся». Это не наука.
Падение тел было бы равномерным
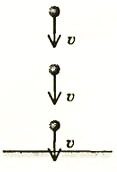
Ограничимся простым случаем падения по вертикали (рис. 6). На камень со стороны Земли действует постоянная сила \(~\vec P\). Как только вы разжали пальцы руки, камень, согласно Аристотелю, тут же начинает падать с постоянной скоростью. С этой же скоростью он достигнет поверхности Земли и немедленно остановится, как только сила упругости со стороны Земли станет равной Р по модулю.
К примеру, в механике Аристотеля прыжки с любой высоты были бы безопасны. Опасность падения с высоты целиком и полностью обусловлена инерцией тел. При достижении силой упругости со стороны Земли значения Р тело не останавливается, но продолжает двигаться вниз, постепенно замедляя скорость. При этом сила упругости со стороны Земли продолжает нарастать, и в теле человека возникают деформации, значительно превышающие те, которые существуют, когда человек стоит на Земле. Это и ведет к травмам.
Не было бы колебаний
Колебания маятника — грузика на нити или на пружине — происходят благодаря инерции тел. Скорость тела по мере приближения к положению равновесия увеличивается, достигает максимума в положении равновесия, но не становится сразу равной нулю после уравновешивания сил. Она уменьшается постепенно благодаря действию силы, направленной к положению равновесия.
Согласно же механике Аристотеля, скорость маятника максимальна в первый момент, когда отклонение от положения равновесия максимально и максимальна сила, действующая на тело. По мере приближения к положению равновесия сила и скорость уменьшаются и в положении равновесия становятся равными нулю.
Можно предположить, что вряд ли возможно существование живых организмов без каких-либо колебательных процессов. Но главная опасность для жизни в другом.
Не существовало бы планетных систем
Если бы по мановению волшебной палочки механика Ньютона сменилась бы на механику Аристотеля, то Земля и все планеты начали бы падать на Солнце со все возрастающей скоростью (рис. 7). Ведь скорость была бы, согласно Аристотелю, направлена по силе, а сила направлена к центру Солнца. И очень скоро с Солнечной системой было бы покончено.
Падения не происходит из-за того, что сила определяет не скорость, а ускорение. Ускорение Земли направлено к Солнцу — в этом смысле Земля «падает» на Солнце, но направленная по касательной к орбите скорость не меняется (в случае круговой орбиты) по модулю, а изменяется лишь по направлению (поворачивается). При сложении ускоренного движения к Солнцу и движения с постоянной скоростью в перпендикулярном направлении получается круговая (или эллиптическая в общем случае) орбита.
Механика Аристотеля и антропный принцип
Почему Вселенная такая, какая она есть? Почему она управляется теми законами, которые мы обнаруживаем? На первый взгляд, эти вопросы кажутся совершенно бессмысленными: не нашего ума это дело. Тем не менее, некий, конечно далеко не исчерпывающий, ответ можно дать. И ответ этот прост: Вселенная должна быть устроена так, чтобы в ней могли появиться разумные существа. В противном случае некому было бы задавать какие-либо вопросы. В этом состоит антропный принцип.
Так вот: антропный принцип «запрещает» механику Аристотеля; механика же Ньютона ему удовлетворяет.
Примечания
- ↑ Кун приобрел всемирную известность, введя в научный обиход звучное греческое слово «парадигма» для обозначения определенной модели деятельности научного сообщества.
- ↑ Дж.Бруно говорил о «множественности обитаемых миров», но для механики обитаемость миров не существенна. Мы и сейчас не знаем, есть ли во Вселенной обитаемые миры кроме нашего.
- ↑ Это утверждение, как и предыдущее утверждение Галилея о сохранении свободным телом постоянной скорости, выполняется только по отношению к инерциальным системам отсчета. Надо полагать, вызнаете, что это такое.