Kvant. Всемирный потоп

Материал из PhysBook

Вышинский В., Стасенко А.Л. Обратная задача Всемирного потопа //Квант. — 2003. — № 3. — С. 35-38.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

сотвори начало не вскоре,- тихо и разумно, со вниманием,

а не борзяся, якоже и умом разумевати глаголемая.

Предварение к Псалтири

Речь пойдет о делах серьезных и весьма давних. Конечно, и в наши дни происходили наводнения в Европе, которые повредили и Праге, и Дрезденской галерее, и Предкавказью... Но в истории Человечества было такое наводнение, которое оставило память на тысячи лет. Вот что читаем в Книге «Бытие»:

«... разверзлись все источники великой бездны, и окна небесные отворились; и лился на землю дождь сорок дней и сорок ночей,., так что покрылись все высокие горы, какие есть под всем небом. На пятнадцать локтей поднялась над ними вода, и покрылись горы. Вода же разливалась на земле сто пятьдесят дней.

... и навел Бог ветер на землю, и воды остановились. И закрылись источники бездны и окна небесные...

Вода же постепенно возвращалась с земли и стала убывать вода по окончании ста пятидесяти дней».

И все это время патриарх Ной (или Ут-Напишти, по вавилонской традиции), предупрежденный загодя Богом, сидел в заранее построенном большом ковчеге (сто лет строил!) со своей семьей и автономным подсобным хозяйством.

«И остановился ковчег в седьмом месяце, в семнадцатый день месяца, на горах Араратских. Вода постепенно убывала до десятого месяца; в первый день десятого месяца показались верхи гор».

Можно ли по этим данным реконструировать численные параметры событий? Задачи такого класса называются обратными или некорректно поставленными. Это не означает, что они плохие. Просто имеет место недостаток входной информации, а решать надо. Картинка внизу наглядно демонстрирует различие между прямой и обратной задачами. И в современном физическом эксперименте такие задачи не редки, так что математики развили целую теорию решения обратных задач. (Приятно напомнить, что тут важнейшую роль сыграла русская школа академика А.Н.Тихонова.)

Прямая задача: описать след известного дракона
Обратная задача: описать дракона по его следу

Попробуем и мы («тихо и разумно...») сделать некоторые физические оценки давно прошедшего события. Итак, дождь шел сорок суток. Примем для оценок, что это был ливень, при котором плотность воды в воздухе порядка \(~\hat{\rho}\) ~ 5 г/м³, а радиус капель a ~ 3 — 5 мм. Такие капли падают со скоростью u - 10 м/с. Значит, плотность потока воды была порядка

\(~\hat{\rho} u\) ~ 5·10^-3 кг/м³ · 10 м/с = 0,05 кг/(м²·с).

За все время t_d такого дождя на каждый квадратный метр пришлось количество воды

\(~\hat{\rho} u t_d\) ~ 0,05 кг/(м²·с) · 40·24·3600 с ≈ 2·10⁵ кг/м²,

что при плотности воды ρ_v = 10³ кг/м³ дало глубину h_d = 200 м. Не мало! Это, скорее всего, оценка сверху. А теперь получим оценку снизу.

Рис. 1

«И продолжалось на земле наводнение сорок дней, и умножилась вода и подняла ковчег и он возвысился над землею».

Если всплывание ковчега произошло в сороковой день, то глубина наводнения в этот момент не могла превышать высоту ковчега в «тридцать локтей». Поскольку древнееврейский локоть равен 44 см, а древневавилонский 49 см, это даст высоту ковчега порядка 13 - 15 м. Таким образом, даже чудовищного ливня, который, пожалуй, на порядок сильнее современного, явно было недостаточно, чтобы затопить «горы Араратские». Тут нужна была помощь Океана. И Бог открыл не только «хляби небесные», но и «хляби земные» - «источники бездны».

Уже слой воды толщиной 10-200 м, образовавшийся от ливня, создал давление на земную кору от одной до десятков атмосфер. Сравним с чем-нибудь. Известно, что во время тайфунов давление воздуха в его центральной части («глаз тайфуна») несколько уменьшается. И даже это небольшое уменьшение (по сравнению с нашей оценкой давления дождевой воды) на больших площадях приводит к разгрузке земной коры, потере ее устойчивости и землетрясениям. Значит, под действием катастрофического ливня одна из тектонических платформ (под Междуречьем) могла опуститься; соседние, возможно, поднялись (кстати, это могло способствовать удержанию прибывающих облаков, как любой горный >хребет не пропускает «тучки небесные, вечные странницы») Так и сказано в писании: «Яко толща земли проседеся на земли». Но как мудро все было устроено: сначала шел обильный, но спокойный дождь - для того, чтобы ковчег (довольно громоздкий ящик, построенный едва ли с учетом теории упругости и сопротивления материалов) плавно оторвался от стапеля и «возвысился над землей», а затем пришла паводковая волна с океана, боковой удар который мог бы разрушить это сооружение.

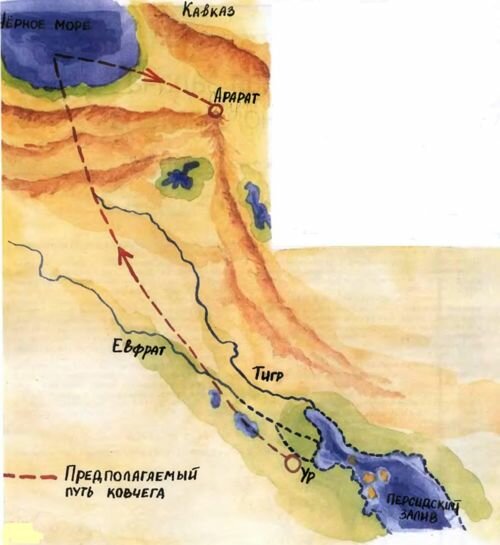
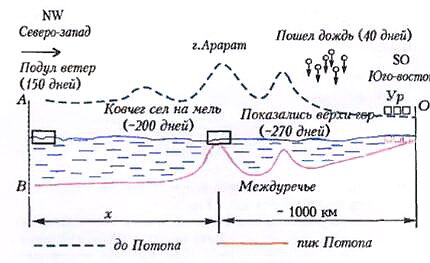
А что же дальше? К сожалению, нам не известно, по какому закону (в зависимости от времени) опускалась суша. Но, поскольку ковчег оказался в конце концов на Кавказе (а о ветре пока не упоминается), разумно предположить, что океанские воды хлынули из Персидского (ныне) залива и погнали ковчег на северо-запад. А от древнего Ура, где жил Ной и все передовое человечество, до Арарата порядка тысячи километров (см. карту древнего, но послепотопного мира, частично изображенную художником на рисунке 1). Правда, ковчег не сразу прибыл туда. Сто пятьдесят дней его тащило куда-то к норд-весту, как сказал бы современный моряк. И тут прибытие воды остановилось. Подул ветер. Конечно, едва ли поверхностный ветер мог быть причиной остановки потока воды глубиной несколько километров. Но не случайно же эти два события указаны как одновременные. И если обитателям ковчега даже только показалось, что ветер остановил поток, значит, он подул с северо-запада (рис.2). А на самом деле он остановиться мог потому, что навстречу с норд-веста шел такой же паводок, так что вертикальная плоскость АВ оставалась неподвижной.

Рис. 2

И только примерно через 200 дней после начала Потопа ковчег «остановился на горах Араратских», хотя суши еще нигде не было видно, т.е. он сел на мель. Значит, более полутора месяцев норд-вест гнал его назад, к зюйд-осту. (На рисунке 1 искривление предполагаемого пути ковчега отражает общую тенденцию всех движений - отклоняться из-за вращения Земли, в частности вправо в северном полушарии, вспомните о крутизне правых берегов наших рек.)

Конечно, если бы мы знали форму ковчега, его осадку, скорость ветра, коэффициент сопротивления,., то можно было бы рассчитать и его траекторию. Но такие сведения даются только великим святым в состоянии «умной молитвы и божественного созерцания». Мы же продолжим приблизительные численные оценки.

Наибольшее расстояние между Тигром и Евфратом, которое, по-видимому, и определяло масштабы расселения тогдашнего «всего Человечества», составляет приблизительно 300 км (см. карту). Поэтому можно предположить, что хлынувший поток имел ширину порядка сотни километров (так говорят физики, когда не знают точно, была ли эта ширина 70 или 400 км). Тут-то и пора воскликнуть: вот это паводок! И приступить к его простенькой теории.

Прежде всего зададимся вопросом: какова была средняя скорость ковчега? Если «паводковая вода» с океана прибывала 150 - 40 = 110 дней и за это время ковчег прошел на NW мимо Арарата приблизительно (1000 + х) км, то его средняя скорость «туда» равна

\(~\upsilon_1 = \frac{1000 + x}{110}\) км/сутки,

а «обратно», под ветром (до посадки на мель на Арарате), -

\(~\upsilon_2 = \frac{x}{50}\) км/сутки.

Если принять эти скорости одинаковыми (а почему нет?), то получим

х ≈ 1000 км .

Значит, ковчег проскочил примерно вдвое дальше, чем расстояние Ур-Арарат. (Если кто-нибудь знает точнее, может сообщить в редакцию «Кванта».) Следовательно, средняя скорость ковчега равна

\(~\upsilon = \upsilon_1 \approx \upsilon_2\) ≈ 20 км/сутки ≈ 0,2 м/с,

А каков должен быть средний секундный расход воды из океана, чтобы за 110 дней заполнить, например, бассейн (см. рис. 2) с поперечным сечением ОАВ, где ОА ~ 2000 км, АВ ~ 5 км (современная высота Арарата над уровнем современного океана составляет 5165 м, но для оценок такие отличия несущественны - тем более, что мы собираемся пренебречь и глубиной наполнения от дождя, которую оценили выше: 10 ≤ h_d ≤ 200 м)? Объем этого бассейна, в расчете на его «ширину» в 1 м_⊥, перпендикулярную рисунку 2, равен

\(~\frac 12 AB \cdot OA \sim \frac 12 \cdot 5 \cdot 2000 \cdot 10^6\) м³/м_⊥ = 5·10⁶ м³/м_⊥ .

Таким образом, «скорость наполнения» была порядка

\(~\frac{5 \cdot 10^9}{110 \cdot 24 \cdot 3600}\) м³/(м_⊥·с) = 500 м³/(м_⊥·с) .

(При таком расходе воды ванна шириной ~ 0,5 м_⊥ и объемом ~ 0,5 м³ наполнилась бы за 2 миллисекунды.)

Оценим теперь потенциальную энергию этого объема воды (тоже в расчете на ширину в 1 м_⊥):

\(~\Pi_1 = \frac{AB}{2} \rho_v V_1 g\) = 5·10³/2 м · 10³ кг/м³ · 5·10⁹ м³/м_⊥ · 10 м/с ² = 1,25·10¹⁶ Дж/м_⊥

(здесь ρ_v - плотность воды). В справочниках можно найти так называемый тротиловый эквивалент: 2 кг этого взрывчатого вещества «обладают» энергией 10⁷ Дж. Тогда найденная потенциальная энергия потока составляет 25·10⁹ кг тротила/м_⊥ , или 25 Мт тротила/м_⊥ . При ширине потока b ~ 100 км = 10⁵ м (см. выше) получим полную потенциальную энергию:

\(~\Pi = \Pi_1 \cdot b\) ~ 2,5·10⁶ Мт тротила ,

что эквивалентно многим тысячам современных самых мощных 100-мегатонных бомб. Поистине, «вздохи» Земли были титаническими.

Впрочем, не бойтесь нового потопа, ибо апостол Петр обещал, что в следующий раз «земля и все дела на ней сгорят». И тогда будет «новая земля и новое небо».

Приложения

1. Рассчитаем скорость капли дождя. В установившемся режиме (при постоянной скорости падения) сила тяжести капли уравновешивается силой сопротивления воздуха. Последняя же, как известно, пропорциональна квадрату скорости движения u, площади поперечного сечения πa² и плотности окружающей среды (воздуха) ρ_voz, т.е. ~ Gu²πa²ρ_voz , где G - безразмерный коэффициент, равный приблизительно 1/4 для сферы. Итак,

\(~u = 4\sqrt{\frac{\rho_v ag}{3 \rho_{voz}}}\) .

откуда получаем

\(~\rho_v \cdot \frac 43 \pi a^3g = \frac 14 \rho_{voz} \pi a^2u^2\) ≈ 10 м/с.

(Для радиуса капли приняты значения а = (3 - 5)/2 мм, плотность воздуха равна ρ_voz = 1 кг/м³.)

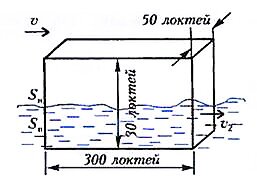
2. Использованная формула для силы сопротивления среды движущемуся в ней телу позволяет оценить и скорость υ ветра, который гнал ковчег к Арарату. Пусть площадь поперечного сечения подводной части ковчега S_p, надводной S_n (рис. 3).