Kvant. Горки, токи и Кулон
Ромишевский Е. Горки, электрические токи и Кулон //Квант. — 1999. — № 1. — С. 31,34-3.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Предметом нашего рассмотрения будут электрические цепи постоянного тока, включающие проводники и источники тока. Но начнем мы с конденсатора.
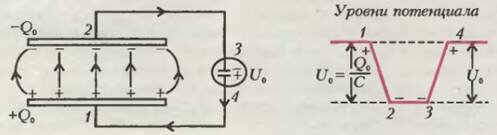
Если подключить к заряженным пластинам конденсатора вольтметр, то цепь, составленная из конденсатора и вольтметра, образует замкнутый контур. А значит, работа по переносу электрического заряда по этому контуру в кулоновском электрическом поле будет равна нулю. Предположим, что вольтметр — идеальный, например электростатический, у которого омическое сопротивление бесконечно большое, а электроемкость бесконечно малая. Двигаясь от положительной пластины 1 к отрицательной 2 (по часовой стрелке — см. рис.1), мы зафиксируем падение (понижение) потенциала на величину \(~U_0 = \frac{Q_0}{C}\), где Q0 - заряд, С - емкость конденсатора. В соединительных проводниках уровень потенциала остается неизменным, а на измерительном элементе вольтметра потенциал поднимается на величину U0. Вот это значение U0 и будет регистрировать идеальный вольтметр — например, по силе притяжения его пластин 3 и 4.
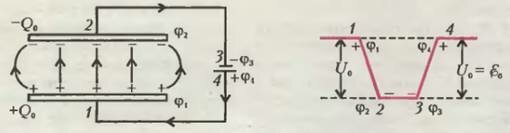
Теперь подключим к пластинам 1 и 2 незаряженного конденсатора источник тока — батарею с электродвижущей силой εb. Конденсатор зарядится до разности потенциалов \(~U_0 = \varepsilon_b = \frac{Q_0}{C}\). Рассмотрим замкнутый контур 1-2-3-4-1 и обойдем его по часовой стрелке (рис.2). Когда мы переходим от положительной пластины 1 с потенциалом φ1, к отрицательной пластине 2 с потенциалом φ2, потенциал уменьшается; следовательно, разность потенциалов \(~\varphi_2 - \varphi_1 = -U_0 = -\frac{Q_0}{C}\) отрицательна. Когда мы переходим от отрицательной пластины батареи с потенциалом φ3 к положительной с потенциалом φ4, эта же разность потенциалов в кулоновском поле батареи положительна: φ4 - φ3 = U0, и мы выходим на тот же уровень потенциала на пластине 1 конденсатора:
Возникает вопрос (вот так всегда бывает с физикой - сплошные вопросы): что же такое эта батарея и какова ее «физическая роль»? Как мы уже говорили, внутри батареи имеется кулоновское поле с разностью потенциалов U0 = εb; значит, там происходит разделение положительных и отрицательных зарядов. Когда мы подключили батарею к незаряженному конденсатору, через нее прошел электрический заряд Q0 (внутри батареи — против кулоновского поля) и потенциал поднялся на более высокий уровень. Какие же силы перемещают заряды против действия кулоновского поля?
Воспользуемся тем, что электрическое кулоновское поле схоже по своим свойствам с ньютоновским полем тяготения. Допустим, что мы (заряды) подошли на первом этаже к лифту (отрицательной пластине батареи). На кабину лифта действует сила тяготения ( сила со стороны кулоновского поля действует на перемещающиеся заряды). Если лифт поднимается равномерно, на него вверх действуют упругие силы натяжения канатов, равные по величине силе тяжести (силе со стороны кулоновского поля). А какой аналог имеют упругие силы канатов лифта, совершающие работу против сил тяжести? Это - силы химической активности, возникающие между металлом пластин батареи и электролитом, ее заполняющим. Эти силы называют сторонними, подчеркивая тем самым их неэлектростатическую природу. Можно ввести напряженность таких сил\[~\vec E_{st}\] - это сторонние силы, действующие на единицу положительного заряда. Поскольку при прохождении зарядов через батарею сторонние силы равны по величине, но противоположны по направлению кулоновским силам, для разности потенциалов можно записать
где lb - расстояние, на котором действуют обе эти силы внутри источника. Значит, εb - это работа, которую совершают силы химической активности, перемещая единицу положительного заряда с отрицательной пластины батареи на положительную против сил кулоновского поля с разностью потенциалов, по величине равной электродвижущей силе батареи, т.е. εb = U0.
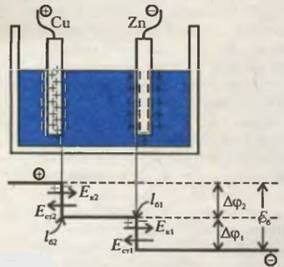
Рассмотрим распределение полей и потенциалов внутри некоторой конкретной батареи (так называемом элементе Вольта — см. рис.3). В непроводящую банку, содержащую водный раствор серной кислоты, вставлены две пластины: цинковая и медная. В результате химического взаимодействия цинка с электролитом положительные ионы цинка уходят в раствор, так что поверхность металла заряжается отрицательным зарядом, а прилегающий слой электролита - положительным. Расстояние между этими слоями lb очень мало (порядка атомных размеров), а разность потенциалов Δφ - порядка одного вольта; следовательно, напряженности кулоновского электрического поля между слоями имеют величины, сравнимые с внутриатомными, и поверхностные плотности этих зарядов тоже очень велики. Точно такие же величины имеют и напряженности сторонних сил в этих слоях, поскольку Ek = -Est. Итак, при переходе единицы положительного заряда с отрицательной пластины в электролит сторонние силы «поднимают» потенциал на более высокий уровень: Δφ1 = Ek1lb1 . В объеме электролита (тока пока нет) уровень потенциала не меняется. Вторая пластина выбрана медной потому, что в результате химического взаимодействия с тем же электролитом "ее поверхность заряжается положительным зарядом, а прилежащий слой электролита — отрицательным. Скачок потенциала здесь Δφ2 = Ek2lb2 - величина того же порядка, что и Δφ1, а их сумма и есть электродвижущая сила этой батареи: |Δφ1 + Δφ2| = εb.
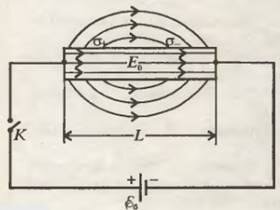
Подключим теперь к клеммам батареи длинный и тонкий однородный цилиндрический металлический проводник, имеющий омическое сопротивление \(~R = \rho \frac lS\), где ρ — удельное сопротивление, L - длина и S - площадь поперечного сечения проводника (рис.4). По этому проводнику потечет постоянный ток \(~I = \frac{\varepsilon_b}{R}\) (если батарея не обладает внутренним сопротивлением). Опять возникает вопрос: какую роль при этом играет электрическое кулоновское поле и какова его картина внутри и вне проводника?
После замыкания ключа по цепи распространяется электромагнитный импульс, который приводит к такому распределению свободных зарядов по поверхности проводника, что внутри него создается однородное электрическое поле напряженностью \(~\vec E_0\) , а вне его — неоднородное поле, силовые линии которого выходят из поверхности проводника и входят обратно под некоторыми углами (см. рис.4). Оказывается, что для однородного длинного и тонкого проводника распределение поверхностной плотности заряда σ вдоль оси проводника (кроме его концов) соответствует линейному закону.
Заметим, что свободные электроны при включении источника тока начинают двигаться практически одновременно во всех участках проводника (подобно тому, как вода начинает двигаться во всех участках водопроводной трубы, когда мы открываем кран). При этом в любой части объема проводника количества положительных и отрицательных зарядов строго одинаковы.
Известно, что при прохождении электрического тока в проводнике выделяется тепло. Каков же механизм перехода химической энергии батареи в тепловую энергию проводника?
В отсутствие источника тока движение свободных электронов в проводнике носит беспорядочный характер. Если же в цепь включен источник тока, на электроны внутри проводника действуют кулоновские силы со стороны электрического поля, которые вызывают упорядоченное, направленное движение электронов. Одновременно со стороны кристаллической решетки действуют силы, тормозящие электроны.[1] Они подобны силам сопротивления движению шарика в вязкой среде (силам жидкого трения). В результате в проводнике устанавливается равномерное движение свободных электронов вдоль силовых линий электрического поля, происходящее с очень маленькой скоростью (по сравнению со скоростью хаотичного теплового движения).
Можно провести аналогию и сказать, что выделение тепла при движении электронов в проводящей среде соответствует выделению тепла при наличии сил жидкого трения, когда за счет сил тяжести (кулоновских сил) тело равномерно соскальзывает с наклонной плоскости. Направление электрического тока соответствует направлению понижения электрического потенциала, т.е. направлению вдоль силовых линий электрического поля. Можно показать (но это несколько выходит за рамки данной статьи), что разность потенциалов на концах проводника равна произведению тока в проводнике на его сопротивление: U = IR.
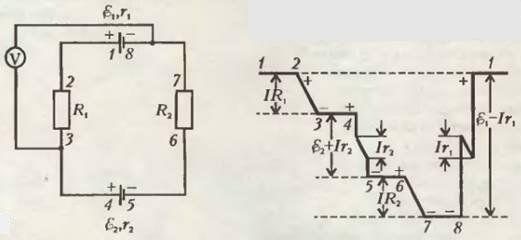
Рассмотрим теперь цепь, состоящую из последовательно соединенных двух батарей с ЭДС ε1, ε2 и внутренними сопротивлениями r1, r2 и двух резисторов с сопротивлениями R1, R2 (рис.5). Пусть ε1 > ε2, тогда ток I в цепи будет течь против движения часовой стрелки. Изобразим изменение потенциала электрического кулоновского поля при обходе по замкнутому контуру.
Точка 1 имеет наивысший потенциал, а точка 8 - наинизший. Проводник 1—2 не имеет сопротивления (нет силы трения), поэтому уровень потенциала здесь не изменяется. Проводник 2—3 с сопротивлением R1 будем считать похожим на наш цилиндрический проводник. На этом участке мы спускаемся «под горку», уровень потенциала линейно понижается от точки 2 до точки 3. При этом сила трения равна «скатывающей» силе - силе со стороны кулоновского поля - и вольтметр покажет U1 = IR1. При движении от точки 3 до точки 4 уровень потенциала не меняется. Точка 4 соответствует нахождению на положительной пластине второй батареи с ЭДС ε2. Когда мы переходим от положительной пластины к электролиту, мы как бы опускаемся в лифте, уровень потенциала понижается, электрическое поле совершает работу против сторонних сил батареи. То же происходит при переходе от электролита к отрицательной пластине. В результате батарея заряжается с мощностью зарядки -ε2I. Движение зарядов внутри батареи связано с преодолением сопротивления r2, и уровень потенциала понижается еще на величину Ir2. Вольтметр, подсоединенный к пластинам этой батареи, покажет U45 = ε2 + Ir2. На участке 5—6 уровень потенциала не изменяется, а на резисторе с сопротивлением R2 потенциал упадет на IR2. И вот мы оказались на отрицательной пластине более сильной батареи с ЭДС ε1 в точке 8. Первый мощный подъем, затем падение на сопротивлении r1 и снова мощный подъем от электролита к положительной пластине 1.
Обойдя замкнутый контур, мы вернулись на начальный уровень кулоновского потенциала. При этом сумма «подъемов» равна сумме «падений» кулоновского потенциала, т.е. работа по замкнутому контуру в кулоновском поле всегда равна нулю:
или
Это соотношение называют законом Ома для замкнутой цепи или вторым правилом Кирхгофа. Теперь мы понимаем, что вообще-то оно непосредственно вытекает из свойств электрического кулоновского поля.
Примечания
- ↑ Подробнее о том, как в металле возникает электрический ток, можно прочитать, например, в статье А.Варламова в «Кванте» № 1 за 1995 год. (Прим. ред.)