Kvant. Движение частиц в полях
Асламазов Л.Г. Движение заряженных частиц в электрическом и магнитном полях //Квант. — 1984. — № 4. — С. 24-25.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
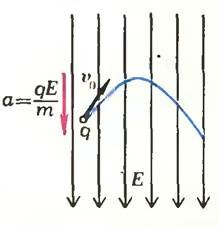
Рассмотрим вначале движение частицы с зарядом q и массой m в однородном постоянном электрическом поле напряженностью \(~\vec E\). Напряженность поля в этом случае не зависит ни от координат, ни от времени (такое поле возникает, например, в заряженном плоском конденсаторе, отсоединенном от источника). Следовательно, на заряженную частицу со стороны поля действует постоянная сила \(~\vec F = q \vec E\), которая сообщает частице постоянное ускорение \(~\vec a = \frac{\vec F}{m} = \frac{q \vec E}{m}\). Если частица имеет начальную скорость \(~\vec \upsilon_0\), как показано на рисунке 1, то ее движение в таком поле похоже на движение тела, брошенного под углом к горизонту в однородном поле тяжести, где ускорение тела также постоянно и равно \(~\vec g\)! В учебнике «Физика 8» показано, что траектория движения в таком случае — парабола.
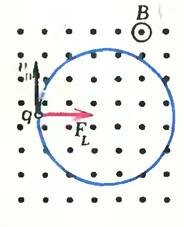
При движении заряженной частицы в однородном постоянном магнитном поле на нее действует сила Лоренца \(~\vec F_L\). Если начальная скорость \(~\vec \upsilon_0\) частицы перпендикулярна вектору магнитной индукции \(~\vec B\) поля, то заряженная частица движется по окружности (рис. 2). Этот случай рассмотрен в учебнике «Физика 9».
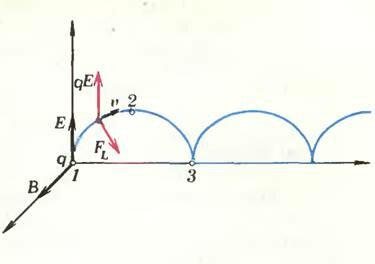
А что если поместить частицу одновременно в электрическое и магнитное поля? Рассмотрим, например, случай, когда напряженность электрического поля \(~\vec E\) и индукция магнитного поля \(~\vec B\) взаимно перпендикулярны, а поля однородны и постоянны (рис. 3). Предположим, что в начальный момент частица находится в начале координат (положение 1) и ее начальная скорость равна нулю. Под действием электрического поля частица начнет ускоряться, то есть приобретет скорость. Сила Лоренца, действующая со стороны магнитного поля, перпендикулярна скорости частицы и поэтому не совершает работы. Она изменяет только направление скорости (искривляет траекторию частицы), но не меняет ее модуля (об этом рассказано в «Физике 9»). В результате после некоторого момента времени (положение 2) частица начнет двигаться в обратном направлении, и электрическое поле будет тормозить ее. В положении 3 скорость частицы опять обратится в нуль, и далее цикл будет повторяться (см. рис. 3).
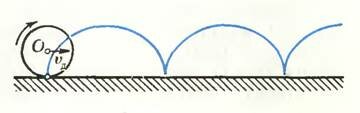
Точный расчет (он довольно сложный и выходит за рамки школьного курса физики) показывает, что траектория частицы в этом случае такая же, как у точки колеса, катящегося с постоянной скоростью без проскальзывания по горизонтальной плоскости (рис. 4; соответствующая кривая называется циклоидой) . Другими словами, движение частицы можно представить как сложение двух движений — равномерного поступательного движения с постоянной скоростью \(~\vec \upsilon_d\) в направлении, перпендикулярном векторам \(~\vec E\) и \(~\vec B\) (ее называют скоростью дрейфа частицы), и вращения вокруг точки О.
Как известно, для описания движения можно пользоваться любой инерциальной системой отсчета. Рассмотрим движение относительно системы отсчета, движущейся со скоростью \(~\vec \upsilon_d\). Относительно этой системы заряженная частица движется по окружности. Вдумайтесь в полученный результат. Мы уже говорили о том, что заряженная частица движется по окружности, когда на нее действует только магнитное поле. Значит, в движущейся системе отсчета электрическое поле исчезает!
В прошлом номере журнала в заметке «Электрическое и магнитное поля» рассказывалось о том, что магнитное поле относительно — его индукция зависит от системы отсчета. Сейчас мы пришли к выводу, что относительно и электрическое поле.