Kvant. Из глубин Вселенной
Стасенко А.Л. Из глубин Вселенной //Квант. — 1996. — № 3. — С. 42-44.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Медленный шопот раздался в его ушах... Словно тихая молния, пронзил его сердце далекий голос, повторявший печально на неземном языке:
— Где ты, где ты, где ты, Сын Неба?
А.Н.Толстой. Аэлита
Когда ученые задумались о возможности радиосвязи с внеземными цивилизациями, среди множества вопросов возник и такой: каким образом представители различных звездных систем могли бы сообщать друг другу информацию, например о своих собственных размерах. Что подумают, скажем, разумные жители систем Альфа Центавра или Тау Кита, если мы выразим свой рост в футах или расстояние между ушами — в локтях? Едва ли им известны эти единицы измерения — тем более что неизвестно, есть ли у них вообще уши, локти или ступни (футы). Не легче обстоит дело и с метрами — ибо это сугубо земная единица длины. И с другими тоже. Следовательно, можно ожидать, что за единицу длины разумные межзвездные корреспонденты должны были бы выбрать некоторую объективную длину, во-первых, одинаковую во всех частях Вселенной и, во-вторых, само понятие о которой должно возникнуть только при определенном уровне развития цивилизации (по крайней мере, когда у последней уже появились радиотелескопы) — а иначе зачем с ней и связываться?
И тут ученые вспомнили о длине волны λ = 21 см, излучаемой нейтральным атомарным водородом. Но — все по порядку.
Еще в 1933 году были обнаружены радиоволны, идущие от центра Галактики, в широком диапазоне длин волн. Директор Лейденской обсерватории Я.Оорт, высоко оценив это открытие, добавил, однако, что неплохо бы найти особую радиочастоту, которая сыграла бы в радиоастрономии такую же роль, как спектральные линии в оптике. И его молодой студент Ван де Хюлст в 1944 году нашел такую частоту: ν = 1420 МГц, что и соответствует длине волны λ = 21 см.
Но что значит «нашел»? Не споткнулся же он о нее на тротуаре Лейдена? Прежде всего, он знал, где искать — конечно, в спектре излучения водорода, которого во Вселенной очень много. Далее, она не должна принадлежать к ультрафиолетовому, видимому, инфракрасному диапазонам спектра — иначе какая же это радиочастота? Потом желательно, чтобы она не генерировалась процессами на Земле — чтобы не было помех... Наверное, что-то в этом роде и думал студент.
Как известно, энергия электрона в атоме может принимать только дискретный набор значений E1, E2, …, En, …, т.е. каждый энергетический уровень имеет свой номер, выражаемый натуральным числом. И если электрон переходит из энергетического состояния n в состояние m, то излучается электромагнитная волна, частота которой νnm или длина волны λnm определяются соотношением
где h = 6,6·10-34 Дж·с — постоянная Планка, с = 3·108 м/с — скорость света в вакууме. Понятно, что в случае излучения должно выполняться условие En > Em, т.е. электрон должен переходить в состояние с меньшей энергией. Если вы рассмотрите кулоновское (электростатическое) притяжение электрона и протона в атоме водорода и учтете правило квантования Бора, то получите радиусы орбит электрона (в частности, нам пригодится r1 = 0,5 А) и дискретный набор оптических частот согласно формуле (1), например серию Бальмера (при m = 2).
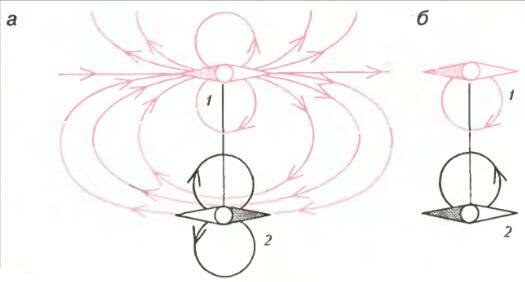
Однако электрон и протон взаимодействуют не только электростатически. Оказывается, каждый из них похож еще и на маленький магнитик. Значит, их взаимодействие будет похоже и на взаимодействие двух магнитных стрелок (рис. 1). Если стрелки расположить рядом, то (в отсутствие магнитного поля Земли) они развернутся антипараллельно: каждая из них расположится вдоль магнитного поля другой стрелки. На рисунке 1,а и изображено это устойчивое положение равновесия (состояние а). Если мы, закрепив стрелку 1, насильно развернем стрелку 2 на 180° (назовем это состояние б) и затем предоставим самой себе, то она обязательно примет прежнее положение. Это означает, что в состоянии а потенциальная энергия стрелки 2 в магнитном поле стрелки 1 меньше, чем в состоянии б: Eа < Eб, хотя расстояния между их центрами одинаковы в обоих случаях. И если на месте этой нижней стрелки представить себе электрон-магнитик, то, согласно формуле (1), он должен излучать электромагнитную волну при таком «перевороте» без изменения расстояния до верхней стрелки (т.е. «радиуса орбиты»).
Конечно, эти макроскопические образы дают только грубый намек на принципиально квантово-механическое явление — излучение радиоволны атомом водорода при «опрокидывании» магнитного момента электрона \(~\vec \mu_e\) относительно магнитного момента ядра (протона) \(~\vec \mu_p\). Но продолжим. Прежде всего, что такое магнитный момент? Уже ясно, что это должен быть некий вектор — ведь при повороте магнитной стрелки на какой-то угол вся картина ее магнитного поля поворачивается на тот же угол. А как описать «силу» магнита, как описать численно тот факт, что один магнит «сильнее» другого?
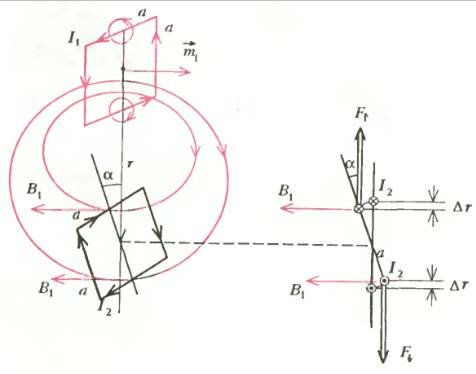
Согласно гипотезе Ампера, магнитное поле стрелки можно объяснить циркулирующими внутренними электрическими токами. Представьте себе для простоты эти токи текущими по квадратной рамке (рис.2). Вектор магнитного момента верхней магнитной стрелки (верхнего контура с током) \(~\vec \mu_1\) направлен так, что с его вершины ток I1, создающий магнитное поле стрелки, направлен против часовой стрелки. (Такой выбор направлений соответствует так называемой правой системе координат, принятой в настоящее время для описания законов физики.)
Найдем магнитное поле, порождаемое током I1 на расстоянии r, много большем, чем размер рамки (r >> a). Как известно из электростатики, величина напряженности электрического поля точечного заряда q на расстоянии r равна \(~E \sim \frac{q}{r^2}\) (закон Кулона). Точно так же в магнитостатике величина магнитного поля, порожденного «точечным» участком тока (ведь a << r), равна \(~B \sim \frac{Ia}{r^2}\) (закон Био—Савара—Лапласа) . А чтобы записать эти зависимости в виде равенств, ставят еще множители, зависящие от выбранной системы единиц — например \(~\frac{1}{4 \pi \varepsilon_0}\) в системе СИ для закона Кулона.
Далее, магнитное поле на расстоянии r порождают все четыре участка с током рамки 1, поэтому получаем
Вот тут уже видна и величина магнитного момента\[~\mu_1 = I_1a^2\]. Если мы выберем систему СИ, то в полученной формуле нужно поставить еще множитель 10-7. Итак, поле магнита с моментом \(~\vec \mu_1\), подобно полю рамки площадью a2 с током I1, и его индукция на большом расстоянии равна
Знак «минус» указывает, что поле в рассматриваемой точке противоположно направлению вектора магнитного момента, создающего это поле.
Пусть теперь в этом месте находится вторая рамка с током I2 («в этом месте» означает, что центр второй рамки расположен на расстоянии r от центра первой рамки, но размер ее конечен — пусть тоже равен а и тоже много меньше r). Легко убедиться, что положением равновесия рамки 2 в поле рамки 1 является такое положение, при котором ток I2 направлен противоположно I1, или вектор магнитного момента \(~\vec \mu_2\) направлен вдоль поля \(~\vec B_1\), созданного первой рамкой. Для этого повернем плоскость рамки 2 на некоторый угол α по отношению к вертикали (см. рис.2). Согласно закону Ампера, на верхнюю сторону рамки действует сила \(~\vec F_{\uparrow} = B_1 I_2 a\), на нижнюю — сила \(~\vec F_{\downarrow} = -B_1 I_2 a\), и они стремятся развернуть рамку в положение α = 0, что и требовалось доказать.
А какую работу нужно совершить для поворота рамки 2 на угол α? Из рисунка видно, что нужно работать против сил \(~\vec F_{\uparrow}\) и \(~\vec F_{\downarrow}\) на двух участках пути длиной \(~\Delta r = \frac{a (1 - \cos \alpha)}{2}\) каждая. Значит, искомая работа равна
И снова видим знакомое произведение I2а2. Теперь-то мы уже знаем, что это модуль вектора магнитного момента \(~\vec \mu_2\)! Поэтому с учетом равенства (2) работу можно записать так:
Видно, что совершенная нами работа зависит от угла поворота рамки 2. Нам особенно интересны случаи α = π и α = 0, когда векторы магнитных моментов параллельны или антипараллельны. При α = π имеем 1 — cos α = 1 — ( —1) = 2, а при α =0 имеем 1 — cos α = 1 — 1 = 0. Следовательно, разность значений потенциальной энергии повернутой рамки 2 в поле рамки 1 для этих двух положений равна
А теперь предположим, что эти наши макроскопические образы применимы для описания системы протон-электрон (нейтральный атом водорода). В справочнике по физике можно найти их магнитные моменты:
(видно, кстати, что электрон как магнит намного «сильнее» протона). Расстояние между ними — это радиус орбиты основного состояния (мы его уже выписывали) r1 = 0,5·10-10 м. Тогда, согласно формуле (1), получим
Конечно, это не точно 21 см, но совсем неплохо, учитывая приближенность классического подхода к такому квантово-механическому явлению, как взаимодействие моментов электрона и ядра. Во всяком случае это радиолиния. В лабораторных экспериментах эту линию получить трудно. Во-первых, трудно получить сам атомарный водород, поскольку при столкновениях атомы будут сливаться в молекулы. Можно, конечно, заставить молекулы, наоборот, диссоциировать на атомы, например нагревая газ до нескольких тысяч градусов. Но это будет газ из возбужденных атомов, а нам они нужны в основном, энергетически наинизшем состоянии. Да и ждать спонтанного поворота магнитного момента электрона долговато (это происходит один раз в 11 миллионов лет). Но в масштабах Вселенной на любом луче зрения находятся миллионы миллиардов триллионов... атомов водорода. И поэтому независимо от того, есть ли разумная жизнь еще где-либо, исследования свечения неба на длине волны = 21 см (или частоте ν = 1420 МГц) имеют особое значение, так как водород — наиболее распространенный элемент во Вселенной. Радионаблюдения нейтрального водорода (спектроскописты обозначают его HI) позволили найти распределение плотности, температуру межзвездной среды (она оказалась порядка 100 К), проекцию скорости движения излучающих масс на луч зрения. Удалось проследить расположение спиральных рукавов нашей Галактики и определить скорость вращения в зависимости от расстояния до центра.
В отличие от электромагнитных волн оптического диапазона (т.е. видимого света), длина которых λ ~ 0,35 — 0,7 мкм сравнима с размерами частиц межзвездной пыли, радиоизлучение на волне 21 см почти не поглощается пылью, что дает возможность «проникать» далеко в область ядра Галактики и даже по другую сторону от него. (Понятно почему: каждая пылинка под действием электрического поля электромагнитной волны поляризуется и колеблется в «такт» с возбуждающим полем волны. Таким образом, она превращается в микроантенну, переизлучающую энергию волны во все стороны. И если размер этой «антенны» сравним с длиной падающей волны, это рассеяние энергии происходит наиболее жадно. А если пылинка-антенна много меньше длины волны, им просто нет дела друг до друга.)
Итак, если вы ждете сообщений от далекой Аэлиты — ждите его на длине волны 21 сантиметр...