Kvant. Как был взвешен атом
Бронштейн М.П. Как был взвешен атом //Квант. — 1970. — № 2. — С. 26-35.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Предисловие
К концу прошлого века в физике и химии утвердилась, как тогда говорили, гипотеза об атомах и молекулах — мельчайших частицах, из которых составлены все тела окружающего нас мира. В химии атомная гипотеза позволила понять и очень удобно описывать химические реакции: всякая реакция — это просто соединение атомов в молекулы или, наоборот, разложение молекул на атомы или группы атомов. Из анализа состава различных молекул химики сумели выяснить, что атомы разных элементов обладают различными массами. Им даже удалось узнать, во сколько раз один атом тяжелее или легче другого; уже к началу второй половины XIX столетия были известны так называемые атомные веса всех открытых к тому времени химических элементов, то есть числа, показывающие, во сколько раз атом данного химического элемента тяжелее самого легкого из атомов - водорода. Знаменитый русский химик Д. И. Менделеев, расположив химические элементы в порядке возрастания атомных весов, показал в 1869 году, что они образуют определенную систему, в которой свойства элементов периодически повторяются (периодическая система). В физике гипотеза об атомах и молекулах играла не менее важную роль. Она позволила физикам составить себе ясное представление о множестве самых различных явлений. Она помогла понять, что такое тепло и холод, почему тела при нагревании расширяются, почему всякое вещество может быть твердым, жидким и газообразным и многое другое. Чтобы все это понять, нужно было только дополнительно предположить, что атомы и молекулы непрерывно и беспорядочно движутся и что между ними действуют силы притяжения и отталкивания. Но при всем этом атомы оставались только некоторым представлением в головах людей. Их не только никто не видел, потому что они очень малы, но никто не знал, насколько они малы, каковы массы атомов, сколько атомов в том или ином теле. Нельзя сказать, чтобы не делались попытки все это как-то узнать. Но эти попытки не приводили к убедительным результатам. У некоторых ученых появилась даже уверенность в том, что об атомах и молекулах ничего и нельзя будет узнать, потому что их на самом деле не существует. Эти ученые полагали, что атомы — это нечто вроде меридианов и параллелей на географической карте: ими удобно пользоваться, но реально в природе их нет. Физики, однако, не теряли надежду доказать реальность атомов и молекул, взвесить их, сосчитать их число, определить их размеры.
В предлагаемом отрывке из книги выдающегося советского физика-теоретика Матвея Петровича Бронштейна «Атомы, электроны, ядра» рассказывается о том, как впервые удалось измерить массу атомов и даже сосчитать их. Эта книга, изданная в 1935 году небольшим тиражом (всего 10 000 экземпляров), давно уже стала библиографической редкостью.
Публикацию подготовил профессор А.К. Кикоин. Сделанные им добавления взяты в прямые скобки.
Как был взвешен атом
... И в конце концов атом действительно удалось взвесить. Этому помогло одно очень странное явление, открытое еще в первой половине XIX века и на которое физики в свое время не обратили должного внимания. Это явление называется брауновским движением.
В 1828 году знаменитый английский ботаник Роберт Браун проделал одно в высшей степени интересное наблюдение. Испытывая только что присланный ему новый усовершенствованный микроскоп с ахроматическим объективом, Роберт Браун вздумал рассмотреть с помощью этого микроскопа ничтожную каплю жидкости, содержащуюся в крохотных зернышках пыльцы растений. В такой жидкости всегда имеется большее количество микроскопических твердых частиц. Как удивлен был Браун, когда увидел, что эти частицы не остаются на месте, а движутся, движутся непрерывно, точно исполняя какой-то фантастический танец! Когда в поле зрения микроскопа было видно много таких частиц, то получалось такое же впечатление, как от тучи каких-то мельчайших мошек. Твердые частицы микроскопических размеров, находящиеся в жидкости, движутся, как если бы они были живыми... Но уже Роберт Браун, который первым наблюдал это хаотическое движение микроскопических частиц, получившее свое название от его имени, пришел к другому заключению: частицы движутся не потому, что они живые... Так утверждал Браун, и это было подтверждено многочисленными последующими наблюдениями.
Можно было бы думать, что брауновское движение микроскопических частиц вызывается какими-то потоками в самой жидкости, связанными с разностью давлений в различных точках жидкости. Всякому приходилось наблюдать движение пылинок в воздухе, освещенном падающими сбоку солнечными лучами. Это движение действительно связано с такими токами воздуха, но брауновское движение имеет совершенно другой характер. В самом деле, если внимательно наблюдать за движением пылинок в солнечном луче, то легко заметить, что соседние пылинки, попавшие в одну и ту же небольшую струю воздуха, движутся в одну и ту же сторону. А если наблюдать за брауновским движением микроскопических частиц, то оказывается, что между направлением движения соседних частиц нет решительно ничего общего: частицы движутся совершенно независимо друг от друга, даже если им случается подойти друг к другу на самое крохотное расстояние, равное диаметру отдельной частички. Значит, совсем не от токов жидкости происходит это непостижимое и фантастическое движение микроскопических твердых частичек.
Во второй половине XIX века брауновское движение подробно исследовал французский физик Гуи. Он проделал целый ряд опытов, которые убедили его в том, что причина брауновского движения скрыта в самой жидкости. Не от внутренних токов жидкости, вызванных ничтожными разностями температур, и не от внешних толчков и сотрясений происходит брауновское движение. Гуи пробовал сравнивать брауновское движение в лаборатории, расположенной на шумной улице, цо которой проезжают тяжелые экипажи, с тем же брауновским движением, наблюдаемым ночью в глухом подвале в деревне. Разницы не получалось никакой. Толчки от экипажей заметны, но они сказываются не на хаотическом движении брауновских частиц, а на движении всей капельки, жидкости в целом: двигаясь, как целое, капелька увлекает за собой все частицы в одном и том же направлении, и это движение очень легко отличить от накладывающегося на него хаотического движения брауновских частиц, происходящего по всем возможным направлениям.
Гуи убедительно доказал, что брауновское движение, как уже предполагал и сам Браун, нисколько не связано с тем, что жидкость, в которой оно наблюдается, взята из живого существа — из растения: искусственно приготовленные жидкости с взвешенными в них микроскопическими частицами, в которых нет ничего живого, тоже обнаруживают брауновское движение. В 1881 году польский физик Бодашевский показал, что брауновское движение происходит и в газах, а не только в жидкостях.
Для того чтобы наблюдать брауновское движение, он рассматривал при боковом освещении микроскопические частички, образующие табачный дым. Крохотные частички угля, из которых состоит дым, плясали во все стороны совершенно таким же образом, как плясали твердые частички, наблюдавшиеся Робертом Брауном в жидкости.
Настоящую причину брауновского движения угадал в 70-х годах прошлого столетия бельгиец Карбонель. Его объяснение, гениальное по своей простоте, состоит в следующем: микроскопические частицы движутся потому, что они испытывают толчки со стороны невидимых молекул и атомов окружающей их жидкости. Рассматривая движение брауновских частичек, мы получаем некоторое представление о том, как движутся невидимые молекулы жидкости, совершенно таким же образом, как мы угадываем о волнении на море, когда, стоя далеко от берега, видим качание лодки, швыряемой волнами во все стороны. Брауновское движение является поэтому мостом, соединяющим невидимый мир атомов и молекул с миром, доступным восприятию при помощи наших органов чувств.
Почему брауновское движение можно наблюдать только в том случае, когда частички очень малы? Очень просто, отвечает на этот вопрос Карбонель; если поверхность частицы велика, то количество толчков, получаемых ею справа, всегда окажется приблизительно равным количеству толчков, получаемых ею же слева, и ничтожное различие в количестве толчков будет совершенно недостаточно для того, чтобы сдвинуть с места большую и тяжелую частицу. Если же частица имеет ничтожную массу и ничтожные размеры, то в хаосе молекулярных движений жидкости всегда может случиться, что с одной стороны частицы будет в данный момент случайно больше толчков, чем с другой, а поэтому легкоподвижная частица двинется в ту сторону, куда ее толкнут молекулы. Через какой-то очень короткий промежуток времени избыток молекулярных толчков будет сдвигать брауновскую частицу уже по другому направлению, еще через какой-то короткий промежуток времени — по третьему и т. д.
Если это предложенное Карбонелем объяснение правильно, то чем частицы легче и мельче, тем брауновское движение должно быть интенсивнее. Так и есть в действительности — уже Браун сумел это заметить. Кроме того, ведь мы знаем, что движение молекул жидкости происходит тем быстрее, чем выше температура; и в самом деле, Гуи нашел, что при повышении температуры брауновское движение делается все интенсивнее и интенсивнее. Когда Жигмонди изобрел ультрамикроскоп и смог наблюдать ничтожнейшие частицы золота в коллоидном растворе (диаметр частиц меньше миллионной доли сантиметра), то брауновское движение этих частиц оказалось таким быстрым, что получилось какое-то сплошное мелькание. Жигмонди описывает свое первое впечатление так: «Это какое-то непрерывное прыганье, пляска, скакание, столкновения и разлетания, так что трудно разобраться в этой путанице»...
Мы переходим теперь к рассказу о классических работах, которые сделал французский физик Жан Перрен (1908 г.). В этих работах было окончательно проверено и установлено,что брауновское движение в жидкостях вызвано движением молекул и тем самым дано решающее доказательство действительного существования молекул и атомов.
Перрен брал кусочки резиновой смолы «гуммигута» и растирал их рукой в воде, пока она не становилась ярко-желтого цвета. После этого Перрен брал немножко такой жидкости под микроскоп. Под микроскопом оказывалась, что гуммигут на самом деле не растворился в воде, а распался на множество шаровидных мелких зернышек, которые разбрелись по всему объему воды. Зернышки эти очень различны по размерам. А Перрену хотелось иметь такую жидкость, в которой были бы совершенно одинаковые по размерам частицы гуммигута. Для этого он воспользовался «центрифугой» (центробежной машиной), такой же самой, какой пользуются на крупных молочных фермах для отделения сливок от молока или же в медицинских лабораториях для удаления кровяных шариков из крови, после чего остается однородная жидкость — кровяная плазма. Центрифуга Перрена делала 2500 оборотов в минуту, и возникающая при этом центробежная сила выбрасывала из жидкости зернышки гуммигута. Перпендикулярно к оси центрифуги были расположены стеклянные пробирки, в которых содержалась эмульсия гуммигута (так называется вода с взвешенными в ней частичками гуммигута).
Первыми выпадали тяжелые частицы, а вслед за ними и легкие. Это давало возможность отделить частицы друг от друга по весу (а значит, и по размерам, потому что все частицы сделаны из одного и того же материала, и поэтому, чем больше их масса, тем больше и размеры).
Это очень кропотливая и тяжелая работа: приходится работать целый месяц для того, чтобы из одного килограмма гуммигута получить несколько десятых или даже сотых долей грамма круглых зерен нужной величины. Таким образом, Перрен сумел получить несколько порций эмульсии с диаметром зерен в 0,5, 0,46, 0,37, 0,21 и 0,14 микрона (микрон — это тысячная доля миллиметра).
С помощью таких эмульсий Жан Перрен произвел множество замечательных опытов, о которых мы здесь и расскажем. Он поместил каплю эмульсии с определенным диаметром зерен в плоскую ванночку (кюветку) с глубиной 0,1 мм. Кюветка была затем покрыта тонким покровным стеклышком, края которого были залиты парафином: таким образом, капля оказалась размазанной в сосуде, в котором она герметически заперта, так что никакое испарение уже невозможно.
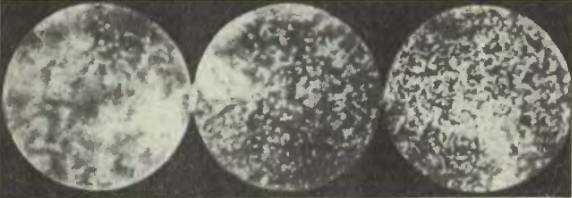
Перрен сперва поставил свою кюветку набок и стал смотреть на нее в микроскоп. В поле зрения микроскопа оказалась тонкая вертикальная водяная стенка, внутри которой распределялись участвующие в брауновском движении зернышки гуммигута. Распределение зернышек сперва было однородным, но потом, с течением времени, распределение изменилось и в конце концов стало таким: очень много зернышек внизу, а по мере продвижения вверх их становится все меньше и меньше (см. рисунок). Число зернышек в одном кубическом микроне уменьшается с увеличением высоты и притом по некоторому вполне определенному закону.
Этот закон уменьшения плотности эмульсии с высотой Перрен захотел исследовать. Для этого он положил кюветку на дно, и после того как частицы расположились по высоте подобно тому, как в кювете, стоящей вертикально, стал смотреть на кюветку сверху в микроскоп, имевший очень маленькую глубину поля зрения: в микроскоп было видно все, что происходит в тонком слое глубиной в один микрон. Передвигая микроскоп вверх и вниз, можно было помещать этот слой то выше, то ниже. Перрен стал работать так: поставил микроскоп на какой-то высоте и начал считать, сколько зернышек виднеется в поле зрения на этой высоте, затем передвинул микроскоп на новую высоту и снова сосчитал число зернышек и т. д. Заметим, что при этом числом зернышек считается среднее из нескольких наблюдений, потому что зернышки движутся совершенно хаотически и, следовательно, их число в поле зрения микроскопа бывает то больше, то меньше в зависимости от случая. Поэтому на одной и той же высоте Перрен производил подсчет зернышек много раз и затем уже вычислял значение, характерное для каждой такой высоты.
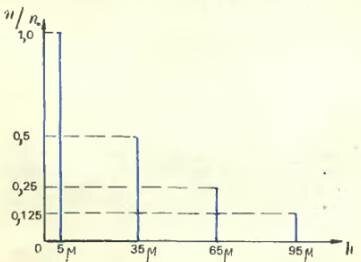
Приведем результаты одного из опытов Перрена. Глубина кюветки была, как мы уже говорили, 100 микрон (то есть 0,1 мм). Отсчеты производились на высотах 5, 35, 65 и 95 микрон над уровнем донышка кюветки. Оказалось, что среднее число частиц на высоте 35 микрон составляет половину того, которое было на высоте 5 микрон, число частиц на высоте 65 микрон было равно половине числа частиц на высоте 35 микрон, а число частиц на высоте 95 микрон равнялось половине числа частиц на высоте 65 микрон. Иными словами, при поднятии вверх на каждые 30 микрон число частиц в данном объеме (соответствующем глубине и ширине выбранного поля зрения) уменьшалось вдвое. Поэтому математический закон убывания плотности (числа частиц в данном объеме, а значит, и в каждой единице объема) с высотой может быть словами выражен так: если высоты образуют арифметическую прогрессию, то числа зерен образуют геометрическую прогрессию.
Такой закон убывания плотности зерен с высотой должен был сильно поразить и заинтересовать Перрена: ведь по такому же самому закону спадает плотность при поднятии в нашей атмосфере. Блэз Паскаль, знаменитый французский ученый, живший в XVII столетии и впервые применивший к изучению атмосферы барометр, изобретенный итальянцем Торричелли, обнаружил закон, по которому спадает с увеличением высоты плотность атмосферного воздуха. Этот закон, получивший название барометрической формулы, гласит то же самое: плотность каждого из газов, составляющих атмосферу, убывает вместе с увеличением высоты в геометрической прогрессии.
[Закон этот можно выразить и математически, в виде формулы.
Предположим, что на какой-то высоте h0 над Землей в каждом кубическом сантиметре содержится n0 молекул какого-то газа. На какой-то другой, большей высоте h таких же молекул в одном кубическом сантиметре будет, конечно, меньше, например n. Тогда барометрическая формула может быть записана в таком виде:
Здесь А — это некоторая постоянная величина, одинаковая для всех газов (при данной температуре), а m — масса молекулы того газа, о котором идет речь, g — ускорение силы тяжести.
Сразу видно, что в левой части равенства стоит отношение чисел частиц в единице объема (правда, под знаком логарифма), а в правой — разность высот. Это и означает, что если высоты образуют арифметическую прогрессию, то числа частиц образуют прогрессию геометрическую.
Выберем такую разность высот h - h0, чтобы число частиц n на высоте h было вдвое меньше числа частиц n0 на высоте h0. Тогда формула (1) примет вид
В таблице логарифмов легко найти, что lg 2 = 0,30103, так что
Если бы было известно численное значение постоянной А, то, подсчитав число частиц в единице объема n и n0 на высотах h и h0, легко было бы вычислить и массу молекулы m, то есть взвесить ее. Правда, сосчитать молекулы мы тоже не можем, но ведь нам и не надо знать каждое из чисел n и n0 в отдельности. Нужно знать только их отношение. А его легко найти, если измерить барометром давления на высотах h и h0: отношение давлений как раз и равно отношению чисел частиц в единице объема. Но дело в том, что величина А во времена Перрена не была известна (именно опыты Перрена и позволили определить ее). Поэтому Перрен мог рассуждать так: известно, например, что] при поднятии на 5 км количество кислорода, находящегося в кубическом сантиметре, уменьшается вдвое; при поднятии на следующие 5 км оно уменьшается еще вдвое и т. д. и т. д. Это — тот же закон, по которому уменьшается с высотой число зернышек гуммигута в кубическом сантиметре эмульсии, но только здесь иные масштабы — вместо 30 микрон здесь мы имеем 5 км. Отчего же здесь получаются другие масштабы?
Слой гуммигутовой эмульсии в 100 микрон — это, в сущности, такая .же атмосфера, но только состоящая не из молекул кислорода или азота, а из зернышек гуммигута, которые уже достаточно велики, чтобы их можно было видеть в микроскоп. Вследствие большей массы этих зернышек (по сравнению с молекулами газа) уменьшение плотности с высотой происходит быстрее, чем в обыкновенной атмосфере, окружающей нашу Землю, а именно (в случае гуммигутовых зернышек диаметром 0,21 микрона) плотность уменьшается вдвое при поднятии на 30 микрон. «Эмульсия,— говорит Перрен, — это атмосфера в миниатюре, тяготеющая к Земле. В масштабе такой атмосферы высота Альп представилась бы несколькими микронами, а отдельные холмы стали бы равны молекулам». Для нас всего важнее, что молекулы этой миниатюрной «атмосферы» — зернышки гуммигута — могут быть взвешены, а это . позволяет вычислить и массу молекул обыкновенного газа. Так Перрен сумел сделать то, что казалось совершенно невозможным, — взвесить молекулы и атомы.
[Из формулы (3) видно, что произведение массы молекулы m на разность высот, между которыми число молекул в единице объема изменяется вдвое, во всех случаях (то есть для любых частиц) равно одной и той же величине \(~\frac{0,30103}{A}\).
Поэтому, если для гуммигутовых зерен разность высот меньше, чем для кислорода в атмосфере, то это потому, что масса гуммигутового зернышка больше массы молекулы кислорода и как раз во столько раз, во сколько раз 5 км больше, чем 30 микрон.]
Проделаем нехитрый расчет... 5 км в 166 миллионов раз больше, чем 30 микрон. Значит, масса гуммигутового зернышка с диаметром 0,21 микрона превышает массу кислородной молекулы в 166 миллионов раз.
Сколько же весит такой гуммигутовый шарик? Это нетрудно рассчитать, если измерить предварительно массу кубического сантиметра гуммигута. При этом расчете не следует забывать, что в опытах Перрена зернышки гуммигута находились в воде, а значит, по закону Архимеда каждый кубический сантиметр гуммигута терял в весе ровно столько, сколько весит кубический сантиметр воды, то есть 1 г. Значит, каждый кубический сантиметр гуммигута был в воде на один грамм легче, чем в воздухе. В результате всех расчетов (которые мы пропускаем) получается, что масса зернышка (с поправкой на закон Архимеда) была равна 8,5·10-15 г. И она в 166 миллионов раз больше массы молекулы кислорода. Значит, масса молекулы кислорода равна 5,1·10-23 г. А так как молекула кислорода в 32 раза тяжелее атома водорода (молекулярный вес кислорода равен 32), то масса атома водорода — этого самого легкого из всех атомов — равна 1,6·10-24 г. В грамме водорода содержится, следовательно, 6·1023 атомов.
[Так атомы и молекулы были не только взвешены, но и сосчитаны!]
Эти цифры, найденные Перреном, позволили связать употреблявшуюся в то время единицу атомного веса — массу атома водорода — с граммом. Масса атома водорода, выраженная в граммах, получилась настолько ничтожной, что ее никак невозможно себе представить, тем не менее она получилась вполне определенной. Атом был взвешен. Важнейшая задача атомной физики была решена.
[Заметим здесь, что цифры, полученные Перреном, конечно, не очень точны. Впоследствии были найдены другие способы определения масс атомов и молекул, и теперь мы располагаем более правильными значениями масс. По современным данным масса атома водорода, например, равна 1,673·10-24 г, а молекулы кислорода — 5,314·10-23 г. Как видите, эти цифры не так уж сильно отличаются от тех, что впервые были получены Перреном.]
Вот какой результат получил Перрен, изучая распределение зернышек гуммигута в гуммигутовой эмульсии в зависимости от высоты. Но всего любопытнее то обстоятельство, что точно такой же результат был выведен с помощью тех же гуммигутовых шариков, но совершенно иным путем, о котором мы также скажем несколько слов.
Брауновское движение в гуммигутовой эмульсии совершается необыкновенно быстро. Нет никакой возможности проследить за движением отдельного гуммигутового зернышка. Поэтому Перрен и не пытался этого делать, а поступал следующим образом: он отмечал на чертеже положение гуммигутового зернышка через определенные промежутки времени, например через каждые 30 секунд, и полученные точки соединял прямыми линиями (хотя на самом деле гуммигутовое зернышко за это время двигалось не по прямой, а по причудливой ломаной линии). Полученные рисунки дают возможность судить о беспорядочности, хаотичности брауновского движения вообще. Но Перрен делал эти рисунки не только для того, чтобы получить наглядную иллюстрацию к брауновскому движению. Его интересовала количественная сторона дела. Знаменитый Альберт Эйнштейн, который был тогда еще молодым человеком, написал (в 1905 — 1906 годах) замечательные работы, где он вывел формулу, определяющую для заданного промежутка времени среднее смещение гуммигутового зернышка относительно его первоначального положения в жидкости. Мы не станем здесь приводить эту замечательную формулу, заметим только, что в эту формулу входит величина, равная числу атомов водорода в одном грамме. Поэтому, сравнивая формулу Эйнштейна с рисунками Перрена, определяющими перемещение частицы за 30 секунд, можно вычислить эту величину. Так и сделал Перрен, и у него получилось, что число атомов водорода в одном грамме равно 6·1023, то есть получилось такое же число, как и раньше.
Совпадение двух чисел, которые были получены совершенно различными способами, является лучшим доказательством правильности всех сделанных предположений. Значит; молекулы и атомы действительно существуют, а не только являются удобной для химиков выдумкой. Такое заключение вынуждены были сделать даже те, которые долго и упорно не хотели признавать существования атомов.
... Вековой спор между сторонниками и противниками атомов закончился, таким образом, победой сторонников атомной теории. И в настоящее время мы можем с уверенностью утверждать, что все вещи на свете — и вода, и камни, и растения, и животные, и воздух, и железо и т. д. и т. д.— все это состоит из мельчайших невидимых глазу атомов.
Задачи к статье
- Пользуясь приведенными в статье данными, найдите, на какой высоте давление уменьшается вдвое. Воздух легче кислорода в отношении 28,8 : 32.
- P0 — давление воздуха на уровне моря, P1 — на высоте h. Каково давление воздуха на высотах: 2h, 3h, nh? Считать, что температура воздуха и ускорение свободного падения не меняются с высотой, и поэтому постоянная А не зависит от высоты.
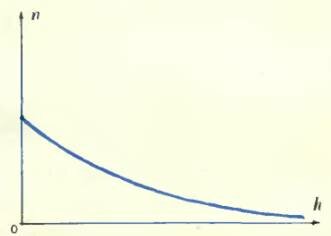
- Найдите высоту над поверхностью Земли, где давление воздуха равно 0,25 и 0,125 атмосферного. Постройте кривую зависимости давления воздуха от высоты.
Ответы
- 5,55 км.
-
\(~P_2 = P_1 \left( \frac{P_1}{P_0} \right)\) , -
\(~P_3 = P_2 \left( \frac{P_1}{P_0} \right) P_1 \left( \frac{P_1}{P_0} \right)^2\) , -
\(~P_n = P_1 \left( \frac{P_1}{P_0} \right)^{n - 1}\) .
-
- 11,1 км; 16,65 км. Удобно воспользоваться результатом задачи 1. Давление пропорционально плотности воздуха.
Примечания
-
↑ Если k — это число «шагов», за которое мы поднимаемся на высоту h, а Δh — высота «шага», то \(~h = h_0 + (k - 1) \Delta h\), а \(~n = n_0 \left( \frac 1q \right)^{k - 1}\), где \(~\frac 1q\) — знаменатель прогрессии, которую составляет плотность газа (q > 1). Из этих двух формул, исключив k, мы найдем, что
\(~\lg \frac{n_0}{n} = \frac{\lg q}{\Delta h} (h - h_0)\) . (*) Аналогичную формулу можно записать и для другого газа; величины, относящиеся к нему, мы снабдим штрихом:
\(~\lg \frac{n'_0}{n'} = \frac{\lg q'}{\Delta h'} (h' - h'_0)\) . (**) Очень важным оказывается то обстоятельство, что, если плотности первого и второго газов уменьшились в одно и то же число раз, то есть \(~\frac{n_0}{n} = \frac{n'_0}{n'}\), то отношение разностей высот, при которых это произошло, \(~\frac{h - h_0}{h' - h'_0}\) в точности равно обратному отношению масс молекул этих газов:
\(~\frac{h - h_0}{h' - h'_0} = \frac{m'}{m}\) . Разделим почленно уравнение (*) на уравнение (**):
\(~1 = \frac{\lg q (h - h_0)\Delta h'}{\lg q' (h' - h'_0)\Delta h} \) , или \(~\frac{\lg q}{\lg q'} = \frac{\Delta h m}{\Delta h' m'} \) . Таким образом, \(~\lg q \sim \Delta h m\). Это дает возможность записать, что
\(~\lg q = A_1 \Delta h m\) . где A1 — это некоторая постоянная величина, не зависящая от величины шага и одинаковая для всех газов (при данной температуре).
Теперь барометрическую формулу (*) мы можем записать в таком виде:
\(~\lg \frac{n_0}{n} = A_1mg (h - h_0)\) .