Kvant. Карусель
Стасенко А.Л. Кинематика на карусели //Квант. — 1994. — № 5. — С. 41-42.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
«Неужели в самом деле все сгорели карусели?» — спрашивается в детской классике. Надеемся, что не все, и вообразим себе такую идиллию: девочка-отличница угощает мальчика вишенками, бросая ему в рот по одной штуке. Расстояние между ними L, угол бросания α, начальная скорость υ0 — все, как на обычном уроке. Но при этом мальчик стоит на вращающейся карусели, прямо в ее центре.
Давайте исследуем траекторию летящей ягоды в двух системах координат; одна из них связана с землей и неподвижной девочкой — назовем ее Д-системой, а другая жестко связана с каруселью и вращается вместе с мальчиком — это М-система. А чтобы не писать скучных формул, выполним построение траекторий графически.
Но прежде уточним исходные данные. Пусть α = 60°, a L, υ0 и скорость вращения выбраны так, что за все время τ полета вишенки карусель с мальчиком сделает два оборота (ясно, что это число оборотов должно быть целым числом, чтобы ягода достигла цели).
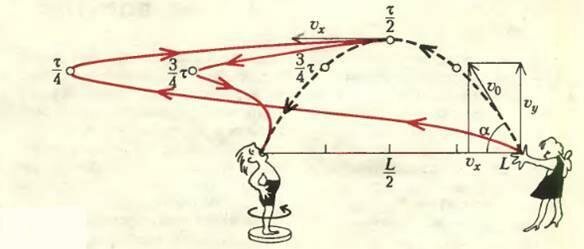
В Д-системе траектория ягоды в вертикальной плоскости будет параболой (вид сбоку), а в горизонтальной (вид сверху) — прямой линией (рис. 1 и 2; черные штриховые линий). В момент бросания t = 0 горизонтальная скорость равна υx = υ0 cos α, а вертикальная υy = υ0 sin α. Конечно, сопротивление воздуха не учтено.
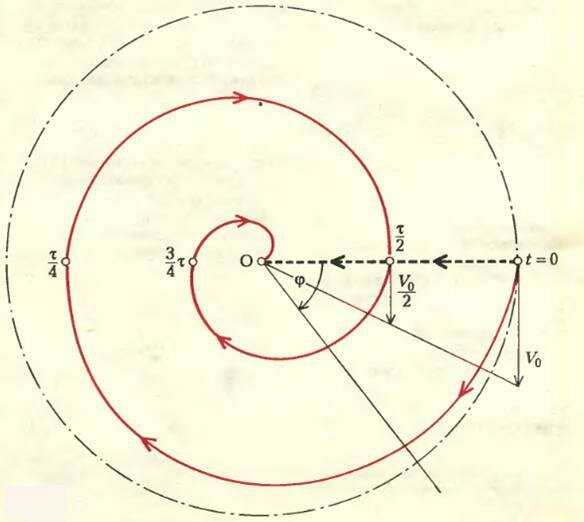
В М-системе мальчик, разумеется, неподвижен, а девочка мчится по окружности в сторону, противоположную вращению, с линейной скоростью \(~V_0 = \frac{2 \pi L}{T}\) и угловой скоростью \(~\omega_0 = \frac{2 \pi}{T}\) (Здесь \(~T = \frac{\tau}{2}\) — период, или время одного оборота карусели.) Траектория девочки в М-системе изображена на рисунке 2 штрих-пунктирной линией. Поскольку скорость вращения постоянна, угловая координата девочки и ягоды (азимут) в М-системе линейно растет со временем\[~\varphi = \omega_0 t = \frac{4 \pi t}{\tau}\].
Отметим несколько характерных точек на траектории ягоды, которые особенно просто построить. Например, ясно, что в момент времени \(~t = T = \frac{\tau}{2}\) вишенка будет находиться в самой верхней точке на расстоянии \(~\frac L2\) от оси вращения. В этой точке ее горизонтальная скорость, постоянная во все время движения, равна υx = υ0 cos α, вертикальная скорость равна нулю, а линейная равна \(~\frac{V_0}{2}\) (так как линейные скорости точек жесткой карусели пропорциональны расстоянию от оси вращения). По истечении времени τ = 2T (через два оборота) ягода окажется на оси, где линейная скорость равна нулю, горизонтальная скорость по-прежнему υx, а вертикальная равна -υy (равна по модулю и противоположна по направлению той, что была в момент бросания).
В моменты времени \(~\frac{\tau}{4}\) и \(~\frac{3 \tau}{4}\) вишенка будет на одной и той же высоте, но, конечно, на различных расстояниях от центра.
Если вы поняли, как построены эти характерные точки, то сможете нарисовать и всю траекторию или научить этому ваш компьютер, а уж он-то изобразит на своем экране любую проекцию траектории. Автор и художник не стали обращаться к компьютеру, поэтому к их рисункам (рис. 1 и 2; красные линии) не нужно подходить слишком строго.
Заметим, что в Д-системе на ягоду действует единственная сила — сила притяжения Земли (ведь силой сопротивления воздуха мы пренебрегли). Но во вращающейся М-системе траектория довольно-таки замысловата, и мальчик может вообразить себе, что на ягоду, помимо тяготения, действуют еще какие-то силы (когда он будет изучать динамику, он назовет их силами инерции — но об этом позже).
А если мальчик будет бросать назад девочке косточки от ягоды под тем же углом α и с той же начальной скоростью? Наверное, вам нетрудно будет изобразить и траектории косточек в обеих системах координат.
Ну а если вместо девочки представить себе ДОТ, вместо мальчика — вращающийся танк, линкор или самолет (которые перебрасываются отнюдь не вишенками), то все это можно назвать модным словом конверсия и сообразить, как можно поставить аналогичную задачу для бортового компьютера.