Kvant. Конденсатор в м. поле
Стасенко А.Л. Зачем быть конденсатору в магнитном поле? //Квант. — 1998. — № 5. — С. 38.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Так уж повелось издавна, что в конденсаторе, этом хранителе зарядов, существует электрическое поле, а в катушке с током - магнитное. Но повесить конденсатор в магнитном поле - такое могло прийти в голову только очень Любопытному ребенку. И не зря - он узнал нечто новое.
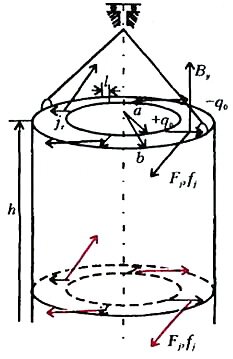
А дело было так. Смастерил Любопытный ребенок конденсатор из двух длинных коаксиальных цилиндров с мало отличающимися радиусами a и b, так что их разность, т.е. ширина зазора b - a = l, много меньше любого из этих радиусов (l << a < b), да и повесил его вертикально в вертикальном же магнитном поле \(~\vec B_y\), причем так, что конденсатор мог вращаться вокруг своей оси совсем без трения (см. рисунок).
На внутренний цилиндр он поместил положительный заряд +q0, на внешний -отрицательный -q0. В результате между обкладками конденсатора возникло радиальное электрическое поле Er. Да вот беда: конденсатор оказался заполненным веществом, обладающим электропроводностью, так что началась утечка заряда и возник радиальный электрический ток. Но на каждый заряд e0, движущийся поперек линий магнитного поля, действует, как известно, сила Лоренца, перпендикулярная обоим векторам — скорости заряда \(~\vec \upsilon_r\) и индукции магнитного поля \(~\vec B_y\), а значит, направленная по касательной к окружности, и равная
(индексы у букв как раз и подчеркивают взаимную перпендикулярность этих трех векторов).
Если концентрация движущихся зарядов n, то на единицу объема будет действовать сила, ее можно назвать объемной плотностью силы,
Поскольку эта сила направлена по касательной, то весь конденсатор начнет вращаться. Цилиндрический слой вещества между обкладками конденсатора и связанные с ним обкладки будут ускоряться в своем вращательном движении под действием суммарной силы, действующей на весь объем 2πalh и равной
(тут-то Любопытному ребенку и пригодилось предположение о тонкости зазора между обкладками конденсатора - а то пришлось бы интегрировать по объему). Итак, уравнение второго закона Ньютона, описывающего ускоренное вращательное движение конденсатора (пусть его масса m) можно записать в виде
Выражение в первой скобке - это плотность тока \(~j_r = ne \upsilon_r\), а во второй - площадь обкладок \(~S = 2 \pi ah\) (она почти одинакова для обеих обкладок, опять же в силу малости зазора между ними). Но если плотность тока умножить на поперечную площадь, получится полный ток \(~I = j_r S\). Таким образом,
Снова не напрасно появились скобки. В скобках справа заключено изменение положительного заряда на внутренней обкладке:
(знак «минус» указывает на тот факт, что положительный радиальный ток уменьшает положительный заряд). Получилось, что приращение импульса конденсатора во вращательном движении \(~d (m \upsilon_{\varphi})\) пропорционально убыли заряда конденсатора. Значит, когда конденсатор полностью разрядится, его «вращательный» импульс достигнет максимально возможной величины
Образованный физик предпочел бы (в случае вращательного движения) говорить не об импульсе (поскольку центр масс конденсатора остается в покое), а о моменте импульса. Он умножил бы силу и импульс силы на плечо a (расстояние до оси вращения) и получил бы совсем грамотное уравнение
для момента импульса конденсатора. Но дело не в этой тонкости (тем более, что Любопытному ребенку многое простительно). Возникает вопрос: откуда взялся вращательный импульс (или момент импульса) у конденсатора, который первоначально покоился? Ведь, согласно фундаментальным законам физики, эти величины не могут уничтожаться или возникать из ничего. Вывод один: они раньше принадлежали электромагнитному полю. В начальный момент конденсатор покоился, но существовали поля Er и By. По мере разрядки конденсатора уменьшалось электрическое поле, и момент импульса электромагнитного поля постепенно переходил к ускоряющемуся (во вращательном движении) конденсатору. Наконец, электрическое поле исчезло совсем, и вместе с этим перестало существовать электромагнитное поле (осталось только магнитное), а конденсатор приобрел наибольшую угловую скорость.
Оказывается, - сказал себе Любопытный ребенок, - электромагнитное поле обладает атрибутами механики: плотностью импульса и момента импульса!