Kvant. Летать дальше или тише

Стасенко А.Л. Как летать: дальше или тише? //Квант. — 2003. — № 5. — С. 28-29.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Войдя в глубокое состояние ЦИГУН,

после определенной тренировки можно понимать язык птиц.

Школа мастера Сюн Минтана

Хорошо, когда есть выбор. Но с чем он связан для крылатых летательных аппаратов (самолетов, птиц)? Попробуем разобраться.

На тело, движущееся в воздухе, действует аэродинамическая сила. Что ж тут удивительного? Ведь «аэро» означает воздух, а «динамис» - сила. Но найти эту силу теоретически очень непросто.

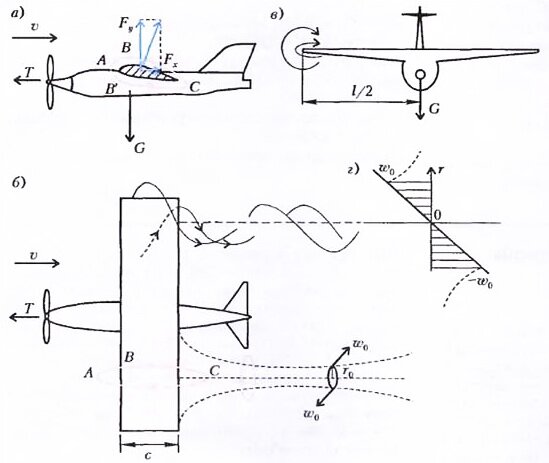
Понятно, что при горизонтальном полете с постоянной скоростью υ ее можно представить в виде векторной суммы двух взаимно перпендикулярных составляющих: вертикальной \(~\vec F_y\), называемой подъемной силой и по величине в точности равной весу \(~\vec G\), и горизонтальной \(~\vec F_x\), которая называется силой сопротивления и должна уравновешиваться силой тяги двигателей \(~\vec T\) (рис. 1,а).

Рис. 1

Далее, легко проверить, что обе эти составляющие пропорциональны произведению ρυ²lc, где ρ - плотность воздуха, lc - площадь крыла самолета (рис. 1,б и в). (Проверьте, по крайней мере, что размерность этого произведения есть ньютон.) Но «пропорциональны» совсем не значит «равны». Любому конструктору самолета хочется, чтобы F_x была поменьше: ведь тогда и мощность двигателя N = F_xυ (значит, и запас горючего) потребуется меньше. Поэтому качество летательного аппарата характеризуют отношением

\(~\frac{F_y}{F_x} = \frac GT\) .

Для современных крылатых летательных аппаратов оно порядка 10 — 20. Это означает, что две составляющие аэродинамической силы «качественного»- летательного аппарата заметно различимы по величине.

Еще на заре авиации, около сотни лет назад, ученые пытались понять, как «устроены» эти силы. И вот что придумали.

Одна из самых изящных идей состоит в том, что подъемная сила крыла связана с так называемой циркуляцией Г:

\(~F_y = \Gamma \rho \upsilon l\) . (1)

Сравнивая с записанным выше выражением для F_y, видим, что Г ~ υc. Немного еще о циркуляции. Когда вода сливается в отверстие ванны, часто образуется вихрь с выделенным направлением вращения (по часовой стрелке или против нее), такой, что на окружности радиусом r скорость воды w(r) одна и та же. Если умножить эту скорость на длину окружности, мы и получим то, что называется циркуляцией:

\(~\Gamma = 2 \pi r w\) . (2)

Во время полета самолета за его крылом образуются два вихря. Действительно, самолет держится в воздухе за счет того, что его крыло, образно говоря, «дует вниз», т.е. создает поток импульса, равный весу летательного аппарата. Масса воздуха, отклоненная вниз, должна вернуться на свое место сверху (см. рис. 1,в), но, поскольку за время этого возвращения самолет улетает вперед, она совершает винтовое движение в системе координат, связанной с самолетом (см. рис. 1,б).

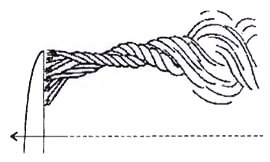
Одно из объяснений подъемной силы таково (см. рис. 1 ,а и б). Масса набегающего воздуха разделяется крылом на две части. Одна из них проходит над крылом путь ABC, больший, чем путь АВ’С той части, которая проходит под крылом. Если мы умножим значение скорости в каждой точке пути АВСВ’А на небольшой участок этого пути и потом все это сложим (в пределе проинтегрируем), то и получим циркуляцию Г. Значит, крыло родило вихрь. А поскольку вихрь в газе или жидкости не может нигде закончиться (разве что замкнуться на себя или на твердую стенку — так называемая теорема Гельмгольца), то с двух концов крыла будут сбегать спутные вихри (см. рис. 1,б), которые на большом удалении могут образовать эллиптические кольца - понаблюдайте за следом самолета в чистом небе. (В частности, еще в 1907 году один из зарубежных азродинамиков - Ланчестер - очень наглядно изобразил процесс сворачивания вихревой пелены крыла; см. рис. 2.)

Рис. 2

Приятно отметить, что зависимость подъемной силы от циркуляции (1) связана с именем русского профессора Николая Егоровича Жуковского.

Рис. 3

А что же сопротивление, т.е. горизонтальная составляющая аэродинамической силы? Прежде всего, оценим так называемое индуктивное сопротивление F_xi, связанное со спутными вихрями. Представим себе вихрь в виде стержня (см. рис. 1,б) радиусом r₀, на поверхности которого окружная (линейная) скорость равна w₀ (а движением воздуха вокруг вихря пренебрежем). Тогда кинетическая энергия единицы объема воздуха в вихре равна \(~\frac{\rho w^2_0}{2} \cdot \frac 12\) (здесь коэффициент \(~\frac 12\) появляется потому, что мы предположили линейную зависимость окружной скорости от радиуса — см. рис.1,г, но это не важно для дальнейшего). Далее, самолет, пролетая в единицу времени расстояние, равное υ, порождает вихревой объем \(~2 \cdot \pi r^2_0 \upsilon\) (так как вихрей - два). А для этого требуется мощность

\(~F_{xi} \upsilon = \frac{\rho w^2_0}{2} \cdot \frac 12 \cdot 2 \cdot \pi r^2_0 \upsilon\) .

Следовательно, сила индуктивного сопротивления равна (см. также (1) и (2))

\(~F_{xi} = \frac{\rho w^2_0}{2} \pi r^2_0 = \frac{\rho \Gamma^2}{8 \pi} = \frac{G^2}{8 \pi \rho \upsilon^2 l^2} = \frac{\alpha}{\upsilon^2}\) ,

где в α входят все характеристики данного самолета (вес, площадь крыла,..). Из последнего выражения видно, что, чем больше скорость полета, тем меньше индуктивное сопротивление, и наоборот. Поэтому при посадке большой самолет порождает мощные вихри над аэродромом, опасные для следующих за ним летательных аппаратов.

Подчеркнем еще раз, что индуктивное сопротивление связано с циркуляцией спутных вихрей. Ведь даже если подъемная сила и, следовательно, циркуляция равны нулю (например, для пикирующего штурмовика), то сопротивление воздуха все равно существует. Это так называемое профильное сопротивление F_xp. Оно пропорционально ρυ²S_⊥, где S_⊥ - лобовое сечение движущегося тела. Видно, что профильное сопротивление тоже связано с квадратом скорости:

\(~F_{xp} = \beta \upsilon^2\) .

Запишем теперь сумму этих двух видов сопротивления:

\(~F_x = \frac{\alpha}{\upsilon^2} + \beta \upsilon^2\) .

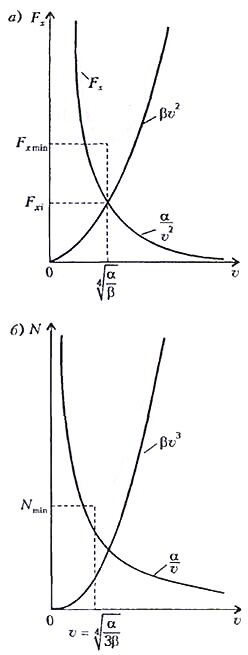
Качественный вид этих зависимостей показан на рисунке 3,а. В частности, легко показать, что суммарное сопротивление достигает минимального значения, когда обе его составляющие равны друг другу, откуда

\(~\upsilon = \sqrt[4] {\frac{\alpha}{\beta}}\)

и

\(~F_{x\ min} = 2 \sqrt {\alpha \beta}\) .

Значит, если мы хотим пролететь как можно дальше, нужно обеспечить равенство профильного и индуктивного сопротивлений в течение всего полета. При этом нужна мощность двигателей

\(~N(F_{x\ min}) = 2 \sqrt {\alpha \beta} \sqrt[4] {\frac{\alpha}{\beta}}\) .

Но, может быть, наша мощность ограничена? Тогда нужно постараться лететь с наименьшей мощностью. Следовательно, нужно найти минимум функции

\(~N = F_x \upsilon = \frac{\alpha}{\upsilon} + \beta \upsilon^3\) .

(рис. 3,б). Можно показать, что ему соответствует скорость \(~\upsilon = \sqrt[4] {\frac{\alpha}{3 \beta}}\) . При этом индуктивное сопротивление составляет уже не половину (как в первом случае), а три четверти от суммарного сопротивления. Подставив найденное значение скорости в формулу для N, получим

\(~N_{min} = \left( \sqrt[4] 3 + \frac{1}{\sqrt[4]{3^3}} \right) \sqrt {\alpha \beta} \sqrt[4] {\frac{\alpha}{\beta}}\) .

Отношение мощностей в двух рассмотренных случаях составит

\(~\frac{N_{min}}{N(F_{x\ min})} = \frac{3^{\frac 14} + 3^{-\frac 34}}{2} \approx 0,87\) .

По-видимому, эти 13% и небезразличны для птиц и двигателей.

Так что «думайте сами, решайте сами», как сказано в одной хорошей песне.