Kvant. Метод электростат. изображений

Черноуцан А.И. Метод электростатических изображений //Квант. — 1987. — № 3. — С. 39-42.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

В школьном курсе физики вы познакомились с явлением электростатической индукции. Вспомним, в чем оно заключается.

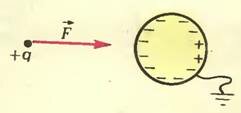
Поднесем точечный заряд +q к какому-либо проводнику, например к незаряженному металлическому шарику. За очень малое время свободные заряды на шарике перераспределятся так, что напряженность результирующего поля внутри него станет равной нулю. После этого движение зарядов прекратится. Поле внешнего заряда оказывается скомпенсированным полем зарядов, «появившихся» на поверхности шарика. Будем называть их наведенными зарядами.

Поле наведенных зарядов есть и вне проводника, в частности, оно действует на заряд +q — заряд притягивается к шарику, хотя полный заряд шарика равен нулю (рис. 1, а). Если бы шарик был заземлен, притяжение было бы сильнее, поскольку на шарике появился бы избыточный отрицательный заряд (рис. 1, б). Этот заряд перетек бы на проводник с земли под действием поля заряда +q.

• 

  а
• 

  б

Рис. 1

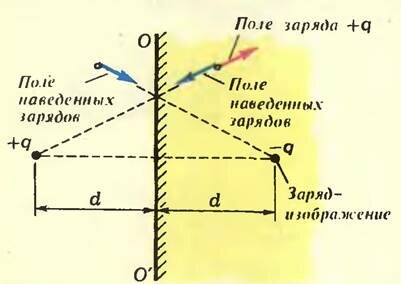
Как рассчитать поле наведенных зарядов? Рассмотрим пример. Пусть проводник занимает все правое полупространство (рис. 2). Тогда на его плоской границе ОО’ соберутся наведенные отрицательные заряды, которые уничтожат поле всюду в проводнике. Вычислить поле вне проводника (слева от ОО’) нам поможет тот очевидный факт, что поле наведенных зарядов симметрично относительно плоскости ОО’. Посмотрите на рисунок 2 — на нем хорошо видно, чему равно поле наведенных зарядов справа от ОО’ (в проводнике). Раз это поле компенсирует поле заряда +q, то, очевидно, оно совпадает с полем воображаемого заряда -q, помещенного в ту же точку, что и заряд +q. Теперь ясно, какое поле создают наведенные заряды слева от ОО’ (вне проводника). Оно в точности равно полю воображаемого заряда -q, но помещенного по другую сторону от плоскости ОО’, симметрично по отношению к заряду +q. Заряд -q называют изображением заряда +q.

Рис. 2

Итак, плоская поверхность проводника притягивает точечный заряд +q, удаленный от нее на растояние d, с такой же силой, с какой его притягивал бы заряд -q, удаленный на расстояние 2d:

\(~F = k \frac{q^2}{(2d)^2}\) .

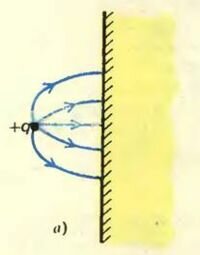
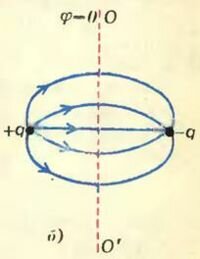
Мы получили удивительный результат: поле, создаваемое зарядом и проводником (рис. 3, а), в пространстве вне проводника совпадает с полем всего двух точечных зарядов (рис. 3, б). Почему оказалась возможной такая подмена? Вспомним, что поверхность проводника представляет собой эквипотенциальную поверхность, причем в нашем примере потенциал проводника равен нулю. Поле же двух зарядов +q и -q обладает следующим свойством: эквипотенциальная поверхность φ = 0 совпадает с плоскостью симметрии ОО’, т. е. точно повторяет форму поверхности рассматриваемого проводника. Именно в этом скрыта причина совпадения полей, изображенных на рисунке 3, а и б. И в других случаях надо стремиться расположить заряды-изображения внутри проводника так, чтобы поверхность проводника совпала с поверхностью постоянного потенциала, равного потенциалу проводника.

• 
• 

Рис. 3

Возникает резонный вопрос — как это сделать? Как найти заряды-изображения и их положения, если известны форма и потенциал проводника? К сожалению, в общем случае такого рецепта не существует, и обычно приходится действовать, как говорят, «с конца» — от зарядов к проводнику.

Возьмем несколько точечных зарядов, рассчитаем их поле, найдем любую эквипотенциальную поверхность φ = φ₀ и заполним пространство внутри этой поверхности проводником с потенциалом φ₀. Тогда поле, которое мы уже рассчитали, представляет собой готовое решение для получившегося проводника и тех зарядов, что оказались вне его! Заряды же, которые «погибли» внутри проводника, играют роль зарядов-изображений. Таким способом можно построить много «готовых» решений, но нет гарантии, что среди них найдется проводник заранее заданной формы.

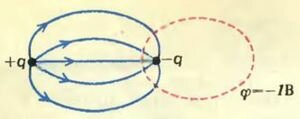
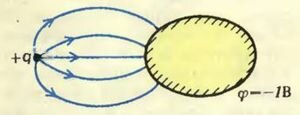
Рассмотрим пример. Возьмем какую-нибудь эквипотенциальную поверхность для тех же зарядов +q и -q, например с φ = -1 В (рис. 4, а). Поле этих двух зарядов вне этой поверхности совпадает с полем заряда +q и проводника, имеющего фиксированный потенциал φ = -1 В (рис. 4, б).

• 

  а
• 

  б

Рис. 4

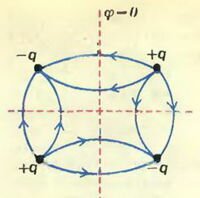
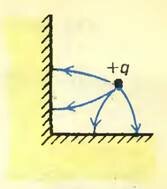
Еще пример. Поле четырех зарядов +q, +q, -q и -q, размещенных в вершинах прямоугольника (рис. 5, в), имеет эквипотенциальную поверхность φ = 0 в виде двух взаимно перпендикулярных плоскостей. Значит, часть этого поля, заключенная в первом квадранте, совпадает с полем заряда +q, помещенного в двухгранный угол (рис. 5, б). Три других заряда являются изображениями заряда +q. Попробуйте сами найти решение для заряда, помещенного в трехгранный угол, — для этого вам придется использовать семь дополнительных зарядов.

• 

  а
• 

  б

Рис. 5

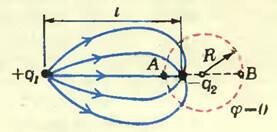
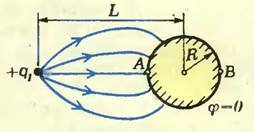
Вернемся теперь к примеру с металлическим шариком, о котором шла речь в начале статьи. Возьмем два заряда +q₁ и -q₂ (q₁ > q₂), расположенные на расстоянии l друг от друга. Оказывается, что эквипотенциальная поверхность φ = 0 представляет собой сферу (рис. 6, а). Чтобы определить радиус этой сферы R и расстояние L от ее центра до заряда +q₁ можно приравнять к нулю потенциалы точек А и В (рис. 6, б):

\(~\begin{matrix} k \frac{q_1}{L - R} - k \frac{q_2}{R - (L - l)} = 0 \\ k \frac{q_1}{L + R} - k \frac{q_2}{R + (L - l)} = 0 \end{matrix}\) . (*)

• 

  а
• 

  б

Рис. 6

Поле этих двух зарядов в пространстве вне сферы в точности совпадает с полем, которое возникает, если заряд +q₁ поместить на расстоянии L от центра заземленного металлического шара радиусом R (рис. 6, б). В этом случае, когда задано положение шара, нам известны R и L, а положение отрицательного заряда-изображения (l) и его величину (q₂) можно найти из той же системы (*):

\(~\begin{matrix} l = L - \frac{R^2}{L} \\ q_2 = q_1 \frac{R}{L} \end{matrix}\) .

Сила, с которой заряд +q₁ притягивается к шару, равна

\(~F = k \frac{q_1 q_2}{l^2}\) .

А как же найти поле и силу притяжения в случае незаряженного шарика? Тогда кроме изображения -q₂ надо поместить в центр сферы еще один воображаемый заряд +q₂. Поле этих трех зарядов вне сферы будет совпадать с полем заряда +q₁ и незаряженного шарика. Почему? Заметим, что поверхность сферы останется эквипотенциальной поверхностью и после добавления третьего заряда. Зато число силовых линий, входящих внутрь сферы, теперь точно равно числу силовых линий, из нее выходящих, — ведь полный заряд внутри сферы равен нулю. Но такому же условию удовлетворяет поле и в случае незаряженного проводника! Значит, мы нашли правильное поле. Сила притяжения заряда +q₁ к шару в этом случае будет заметно меньше — ведь он не только притягивается к изображению -q₂, но и отталкивается (с меньшей силой) от другого изображения +q₂:

\(~F = k \frac{q_1 q_2}{l^2} - k \frac{q_1 q_2}{L^2}\) .