Kvant. М. сила и закон ЭМИ

Ромишевский Е., Стасенко А.Л. Магнитная сила и закон электромагнитной индукции //Квант. — 2008. — № 5. — С. 38-40.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Лаплас присутствовал на первой публичной демонстрации опыта Ампера.
Публика уже расходилась, и Лаплас у выхода стал ждать ассистента...
хлопнул его по плечу и, пристально глядя на него, спросил:
«А не вы ли это, молодой человек, подталкивали провод?»
М. Льоцци. История физики

К настоящему времени уже миллиарды людей воспользовались услугами электропоездов, автомобилей, автобусов, самолетов, кораблей, электростанции и т.п., в которых неустанно вращаются роторы электромоторов и генераторов тока. В основе работы этих старательных тружеников лежат фундаментальные законы электромагнетизма, открытые замечательными учеными девятнадцатого века. Вспомним Вкратце лишь о тех из них, о которых пойдет речь в этой статье.

Андре Мари Ампер (1775-1836) открыл взаимодействие электрических токов и установил соответствующий закон, разработал теорию магнетизма (1820).

Майкл Фарадей (1791-1867) в 1821 году впервые осуществил вращение магнита вокруг проводника с током, а также, наоборот, проводника с током вокруг магнита, создав, таким образом, принципиальную модель электродвигателя. В этом несложном опыте была наглядно показана связь между электрическими и магнитными явлениями. Через десять лет он уже открыл явление электромагнитной индукции - возникновение тока в замкнутом проводнике при изменении магнитного потока через контур этого проводника.

Эмилий Христианович Ленц (1804-1865) в 1833 году установил правило определения направления индукционного тока (правило Ленца).

Кстати сказать, и Ампер, и Фарадей, и Ленц были членами Петербургской Академии наук.

Хендрик Антон Лоренц (1853-1928) дал выражение для силы, действующей на движущийся заряд в электромагнитном поле (сила Лоренца). Иностранный член Академии наук СССР.

Продемонстрируем «работу» законов, открытых этими физиками, в самом простом случае поступательного движения проводника в постоянном магнитном поле. Сила Лоренца «направляет» в разные стороны движущиеся электрические заряды разных знаков, а значит, создает в пространстве кулоновские электрические поля и в проводящей среде возбуждает электрические токи, т.е. является создателем источников электрических токов.

Рис. 1

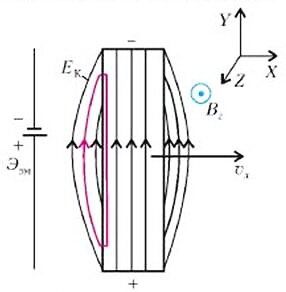
Рассмотрим такой пример. В однородном горизонтальном магнитном поле \(~\vec B_z\), поступательно движется вертикальный длинный проводящий стержень длиной l с постоянной скоростью \(~\vec \upsilon_x \perp \vec B_z\); (рис. 1); (Здесь индексы удобно указывают направления соответствующих векторов в декартовой системе координат XYZ. Кружок с точкой означает, что ось Z и магнитное поле направлены к нам.) Положительные ионы (к примеру, ионы меди Cu⁺) закреплены в узлах кристаллической решетки, а свободные электроны, перемещаясь вверх под действием магнитной силы Лоренца \(~\vec F_L = e (\vec \upsilon_x \times \vec B_z)\), создают в объеме проводника однородное кулоновское электрическое поле \(~\vec E_K = (\vec \upsilon_x \times \vec B_z)\), уравновешивающее действие магнитной силы. (Заметим, что здесь учтен отрицательный заряд электрона, равный -е, где е = 1,6•10^-19 Кл - положительная фундаментальная константа.) В результате между концами стержня возникает постоянная разность потенциалов, равная \(~E_K l = \upsilon_x B_z l\). Таким образом, создается «электромагнитная батарейка» с электродвижущей силой \(~\varepsilon_{em} = \upsilon_x B_z l\) и сторонней (т.е. не кулоновского происхождения) напряженностью.

А что это за изогнутые линии с боку от стержня? Они нарисованы для того, чтобы подчеркнуть существенное отличие кулоновского поля от сторонних полей: работа по перенесению пробного заряда в кулоновском поле но замкнутому контуру (выделен цветом) равна нулю. Заметим, что электродвижущие силы (ЭДС) и связанные с ними сторонние напряженности в своей основе опять-таки имеют электромагнитный характер, но уже другого (тоже некулоновского) рода.

Рис. 2

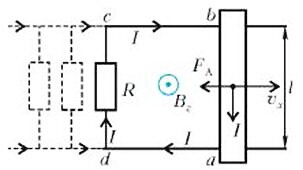
Теперь используем эту «электромагнитную батарейку» для получения электрического тока и электрической энергии. Для этого будем двигать наш стержень вдоль двух параллельных горизонтальных проводников, находящихся на расстоянии l друг от друга (рис. 2). Проводники замкнем на резистор сопротивлением R. Причем двигаться будет только стержень, а проводники и резистор должны быть неподвижными. (Иначе в них тоже будет создаваться «электромагнитная батарея» той же силы, что и возникающая в стержне, но противоположно «направленная», так что тока в замкнутом контуре не будет.) Тогда в замкнутом контуре abcd потечет электрический ток \(~I = \frac{\varepsilon_{em}}{R}\), и на сопротивлении R будет выделяться тепловая мощность \(~I^2R\).

За счет чего же выделяется тепловая энергия, и справедлив ли здесь закон сохранения энергии?

По движущемуся стержню сверху вниз течет электрический ток I. Значит, на проводник с током, находящийся в однородном магнитном поле \(~\vec B_z\), действует сила Ампера, направленная противоположно направлению движения стержня, т.е. вектору \(~\vec \upsilon_x\). Чтобы стержень сохранял постоянную скорость движения υ_x, к нему необходимо приложить силу \(~\vec F^*\), равную по величине силе Ампера \(~F_A = IB_zl\), но направленную противоположно ей. При этом мощность этой силы (\(~N = F^* \upsilon_x = IB_zl \upsilon_x = I^2R\)) в точности равна тепловой мощности, выделяющейся па сопротивлении R, что, конечно же, неудивительно. Закон сохранения энергии верен!

Подключим теперь к параллельным проводам, по которым скользит стержень, еще один резистор сопротивлением R (см. рис. 2). Тогда, если стержень по-прежнему будет двигаться со скоростью υ_x, через него уже потечет электрический ток величиной 2I. Сила Ампера увеличится в два раза, и в два раза больше станет выделяющаяся на сопротивлениях тепловая мощность. Таким образом, мы получили электрический генератор постоянного тока. Включение нескольких параллельных сопротивлении R во столько же раз увеличит силу Ампера, тормозящую стержень.

Рис. 3

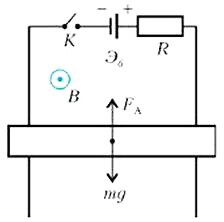
Расположим теперь параллельные проводники вертикально (рис. 3), и пусть по ним скользит наш проводящий (уже горизонтальный) стержень массой m, замыкающий цепь с резистором сопротивлением R и аккумуляторной батареей с электродвижущей силой ε_b. Контур пронизывается прежним однородным горизонтальным магнитным полем \(~\vec B\), направленным к нам, и находится в поле тяготения Земли. (Индексы для векторов и их проекций для простоты опустим, так как мы уже разобрались что куда направленно.) Если замкнуть ключ К и отпустить стержень, то по цепи потечет ток \(~I = \frac{\varepsilon_b}{R}\), направленный по часовой стрелке. Если величина ε_b будет достаточно большой, то сила Ампера, действующая на стержень, будет больше силы тяжести mg, и стержень начнет двигаться вверх с начальным ускорением а, определяемым равенством

\(~ma = F_A - mg\) .

Если скорость стержня υ, он превращается в «электромагнитную батарейку», имеющую электродвижущую силу \(~\varepsilon_{em} = \upsilon Bl\) и «действующую», по правилу Ленца, против вызывающей ее причины, т.е. против ε_b. В койне концов может установиться стационарное состояние (отметим его индексом 0):

\(~I_0Bl = mg, I_0R = \varepsilon_b - \varepsilon_{em} = \varepsilon_b - \upsilon Bl\) , (*)

откуда получим постоянную скорость движения стержня:

\(~\upsilon_0 = \frac{\varepsilon_b Bl - mgR}{(Bl)^2} = \frac{\varepsilon_b}{Bl} \left( 1 - \frac{mgR}{\varepsilon_b Bl}\right)\) .

Если первое равенство выражения (*) умножить на υ₀, а второе - на I₀, мы опять получим закон сохранения энергии:

\(~\varepsilon_b I_0 = \varepsilon_{em} I_0 + I^2_0R = mg \upsilon_0 + I^2_0R\) .

Видно, что мощность аккумуляторной батареи расходуется на полезную мощность поднятия груза массой m со скоростью υ₀ и на выделяющуюся при этом тепловую мощность. Таким образом, на рисунке 3 фактически изображена принципиальная схема электрического мотора: ведь к нашему проводящему стержню вполне можно прикрепить, например, ведро волы, поднимаемое из колодца.

Итак, полезная (механическая) мощность нашего мотора равна

\(~N_{pol} = \varepsilon_{em} I_0 = \frac{\varepsilon_{em} (\varepsilon_b - \varepsilon_{em})}{R}\) ,

следовательно, его коэффициент полезного действия равен

\(~\eta = \frac{N_{pol}}{N_z} = \frac{\varepsilon_{em} I_0}{\varepsilon_b I_0} = \frac{\varepsilon_{em}}{\varepsilon_b}\) ,

где N_z - полная мощность, затрачиваемая батареей.

Рис. 4

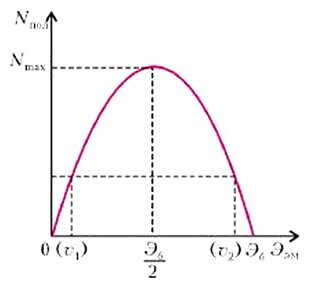
На рисунке 4 изображен график зависимости полезной мощности от ε_em в нашем случае от \(~\varepsilon_{em} = \upsilon Bl\). Это - парабола. Легко видеть, что максимальная полезная мощность мотора N_max достигается, когда «электромагнитная» ЭДС ε_em оказывается в двое меньше ЭДС включенной в цепь батареи ε_b. При этом коэффициент полезного действия мотора составляет \(~\frac{\varepsilon_{em}}{\varepsilon_b} = 0,5\), т.е. 50%. Это значит, что если мы имеем электрический мотор, в цепи которого содержится батарея с ЭДС ε_b и сопротивлением R, и он поднимает груз массой m, то максимальную скорость поднятия этого груза можно найти так:

\(~mg \upsilon_{max} = \varepsilon_{em} I_{max} = \frac{\varepsilon_b}{2} \frac{\varepsilon_b - \frac{\varepsilon_b}{2}}{R} = \frac{\varepsilon^2_b}{4R}\), и \(~\upsilon_{max} = \frac{\varepsilon^2_b}{4mgR}\).

По графику рисунка 4 видно, что одну и ту же полезную мощность с одним и тем же мотором можно получить, поднимая быстро (υ₂ > υ₁) легкий груз или медленно - тяжелый груз. Причем поднимать быстро легкий груз значительно выгоднее, потому что коэффициент полезного действия может быть значительно больше и мотор при этом будет греться существенно меньше. Максимально возможная скорость движения бесконечно легкою груза (mg → 0 ) достигается, когда \(~\varepsilon_{em} = \upsilon^* Bl = \varepsilon_b\), при этом I → 0 и КПД → 1. Эту скорость \(~\upsilon^* = \frac{\varepsilon_b}{Bl}\) называют скоростью холостого хода мотора.

Вернемся снова к схеме «электромотора» (см. рис. 3). Эту схему очень просто превратить в схему «генератора», поменяв полюса батареи. Если в начальный момент замкнуть ключ и отпустить стержень, то вначале сила Ампера будет направлена вниз, и стержень будет падать с ускорением, большим ускорения свободного падения:

\(~ma = mg + IBl\) ,

когда \(~\varepsilon_{em} = \upsilon Bl\) станет больше ε_b, и в дальнейшем установится стационарное состояние:

\(~\upsilon_{ust} Bl - \varepsilon_b = I_{ust} R, mg = I_{ust} Bl, \upsilon_{ust} = \frac{\varepsilon_b}{Bl} \left( 1 + \frac{mgR}{\varepsilon_b Bl}\right)\) .

При этом за счет уменьшения потенциальной энергии стержня в поле тяжести начнет заряжаться батарея и, кроме того, будет выделяться тепловая мощность на сопротивлении. На языке мощности запишем:

\(~mg \upsilon_{ust} = \upsilon_{ust} Bl I_{ust} = \varepsilon_b I_{ust} + I^2_{ust} R\) .

Рассмотренные примеры убедительно показывают, что такие важные для человечества физические объекты, как электрические генераторы и электрические моторы, являются как бы «родственными» по линии магнитных сил Лоренца и Ампера.

Обобщим теперь полученные результаты. Вернемся к нашему начальному примеру, изображенному на рисунке 2. Параллельные провода и перемычка с резистором сопротивлением R неподвижны. Стержень длиной l движется со скоростью υ_x. В данный момент времени t координата стержня равна х. Магнитный поток Ф(t) через замкнутый контур abcd равен произведению индукции поля B па площадь lx(t) перпендикулярной нолю площадки:

\(~\Phi(t) = Blx(t)\) .

Заметим, что

\(~\frac{d \Phi}{dt} = Bl\frac{dx}{dt} = Bl \upsilon_x\) .

Значит, можно записать, что

\(~\varepsilon_{em} = -\frac{d \Phi}{dt}\) .

Почему стоит знак «минус»? В нашем случае магнитный поток увеличивается, так как увеличивается площадь контура abсd, а ток в контуре будет течь против часовой стрелки и создавать внутри контура собственное магнитное поле, по направлению противоположное магнитному полю В. Это положение и называется правилом Ленца. Нашу электромагнитную электродвижущую силу ε_em назвали электродвижущей силой электромагнитной индукции, а установленный опытными фактами закон

\(~\varepsilon_i = -\frac{d \Phi}{dt}\)

- законом электромагнитной индукции Фарадея.

Дальнейшее обобщение закона (это опять-таки установлено опытными фактами) говорит о том, что если поток Ф магнитного поля \(~\vec B\) через любую поверхность, опирающуюся на замкнутый контур, зависит от времени, то в этом контуре возникает ЭДС электромагнитной индукции, определяемая законом Фарадея. Причем со временем могут изменяться (в отдельности или одновременно) форма контура, его площадь, ориентация в пространстве относительно магнитного поля \(~\vec B\), а также само магнитное поле B(t), которое в общем случае должно складываться из внешнего магнитного поля и собственного магнитного поля, создаваемого возникающим собственным электрическим током в проводящем контуре.

Если вы запомните предыдущий абзац, то прослывете в школе большим знатоком физик. Чего вам и желаем.