Kvant. Номограммы
Шапиро А.И. Номограммы в геометрической оптике //Квант. — 1986. — № 11. — С. 20-22.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Из школьного курса физики вы узнали о том, как можно графически решать различные задачи геометрической оптики. Например, чтобы найти положение изображения точечного источника света в тонкой линзе, достаточно построить ход двух произвольных лучей, вышедших из источника и прошедших через линзу.
В этой заметке будет рассказано еще об одном, несколько необычном графическом способе решения подобных задач. При этом на предлагаемых вам рисунках вы не увидите ни световых лучей, ни оптических осей линзы, ни даже самой линзы. О каких же тогда графиках пойдет речь?
В математике существует специальный раздел, называемый номографией (от греческих слов nomos — закон и grapho — пишу), в котором изучаются методы построения особых чертежей — номограмм. С их помощью можно, например, не производя вычислений, получать приближенные решения уравнений или находить приближенные значения интересующих нас функций. Воспользуемся и мы такой возможностью.
Пусть светящийся предмет находится на расстоянии d от линзы с фокусным расстоянием F, а его изображение — на расстоянии f. Можно показать (это сделано в § 60 «Физики 10»), что эти три величины связаны простым соотношением — формулой тонкой линзы:
Заметим, что каждое слагаемое, входящее в формулу, может быть как положительным, так и отрицательным. Если предмет, или его изображение, или фокус линзы действительные, величины d, или f, или F берутся со знаком «плюс», в случае же если предмет, или изображение, или фокус линзы мнимые, соответствующие величины считаются отрицательными.
Построим номограмму для формулы линзы и покажем, как с ее помощью можно решать конкретные задачи.
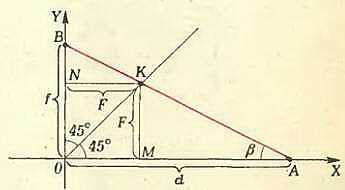
.Изобразим на плоскости прямоугольную систему координат XOY (рис. 1). По оси X отложим отрезок ОА длиной d, а по оси Y — отрезок ОВ длиной f. Пока для определенности d и f будем считать положительными. Соединим точки A и В отрезком прямой, проведем биссектрису прямого угла АОВ и найдем точку К ее пересечения с АВ. Из точки К опустим на оси координат перпендикуляры и обозначим длину полученных равных отрезков КМ и KN через F.
Из подобия треугольников АОВ и АМК следует, что
или
откуда легко получается знакомое нам уравнение (*).
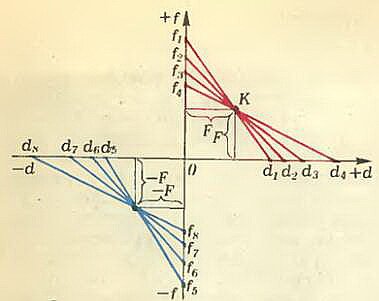
Таким образом, мы получили, что длины d, f и F построенных на чертеже отрезков связаны между собой уравнением тонкой линзы (вот почему при построении мы использовали именно такие обозначения длин отрезков). А это, в свою очередь, означает, что мы умеем строить номограмму для формулы линзы. Действительно, если по горизонтальной оси прямоугольной системы координат откладывать расстояния d от предмета до линзы, а по вертикальной оси — расстояния f от линзы до изображения, то все прямые, соединяющие концы соответствующих отрезков, пересекаются в одной точке (рис. 2). Проекции этой точки на оси координат одинаковы и равны фокусному расстоянию F данной линзы.
Как вы знаете, для определения прямой на плоскости достаточно знать всего две принадлежащие ей точки. Поэтому с помощью построенной номограммы по известным двум из трех величин d, f и F всегда можно графически определить недостающую третью. Так, например, при построении, приведенном на рисунке 1, мы фактически определили фокусное расстояние линзы (F) по известным расстояниям от линзы до предмета (d) и от линзы до изображения (f).
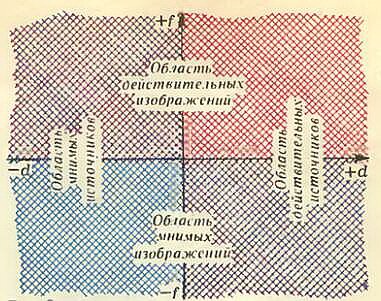
Легко убедиться в том, что предложенный способ годится не только для собирающих линз, но и для рассеивающих, а также для любых расположений предмета и изображения относительно линзы. Если, например, предмет или изображение мнимые, то соответствующие значения d или f являются отрицательными и, следовательно, их надо откладывать в отрицательном направлении от начала координат (влево или вниз). Может случиться, что точка К пересечения всех отрезков, соответствующая фокусу линзы, будет иметь отрицательные проекции. Это будет означать, что фокус линзы — мнимый, то есть что линза — рассеивающая. Области расположения действительных и мнимых предметов и изображений показаны на рисунке 3.
Номограммы можно использовать и для определения линейного увеличения линзы — отношения линейного размера Н изображения к линейному размеру h предмета\[~\Gamma = \frac{H}{d} = \frac{f}{d}\] (см. § 60 «Физики 10»). Из рисунка 1 видно, что
Таким образом, изображение может быть увеличенным, уменьшенным или такого же размера, как и сам предмет. Можно решить и обратную задачу — по заданному увеличению и известному фокусному расстоянию линзы определить расстояния d и f. Для этого достаточно построить знакомую нам точку К и провести через нее прямую, наклоненную к горизонтальной оси под углом β. Точки пересечения этой прямой с осями координат и дадут нам искомые значения d и f.