Kvant. Остановка Земли

Стасенко А.Л. Как Студент думал Землю остановить //Квант. — 2006. — № 5. — С. 28-29.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Бывает, что усердие превозмогает и рассудок.

Козьма Прутков

Однажды под утро подумалось студенту: есть же на Земле такие счастливые места, где ночь длится полгода! И тут пришла ему в голову Идея: остановить вращение Земли — чтобы утро вообще не наступило. Ведь повернута же Луна к нам только одним своим полушарием.

Понятно, что затормозить вращение можно, например, при помощи реактивной силы выбрасываемой массы. Но какую массу для этого придется выбросить в космос? С какой скоростью? И вот, чтобы не утруждать себя деталями, в «тонком полусне» Студент сделал простые численные оценки.

Рис. 1

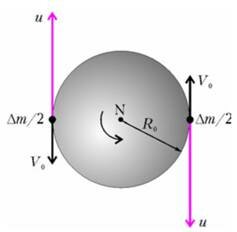
Ясно, что искомую массу Δm нужно выбрасывать симметрично относительно оси вращения — чтобы не изменить движение центра масс Земли. И, конечно, противоположно направлению ее окружной (линейной) скорости V₀. Например, так, как изображено на рисунке 1, где N — северный полюс, а u — искомая скорость выброса относительно Земли. В системе неподвижных звезд скорость выброса будет равна u - V₀.

Рис. 2

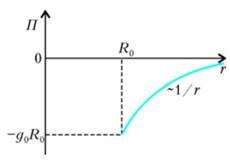
Для того чтобы выброшенная масса не возвратилась, ее скорость на бесконечном удалении от Земли должна по крайней мере обратиться в ноль. Значит, там равна нулю ее кинетическая энергия. Но и потенциальная энергия П там тоже равна нулю — см. рисунок 2, где -g₀R₀ это потенциальная энергия единицы массы на поверхности Земли. Следовательно, закон сохранения полной механической энергии единицы массы можно записать в виде

\(~\frac{(u - V_0)^2}{2} + (-g_0R_0) = 0 + 0\) .

Отсюда находим

\(~u = \sqrt{2g_0R_0} + V_0\) .

«Конечно, это только оценка, — успокоил себя Студент, — ведь в процессевыброса будет изменяться и масса Земли, и ее радиус, и, следовательно, ускорение тяготения на поверхности». (Поэтому величины V, g, R и отмечены индексом «0» — чтобы подчеркнуть, что для оценки берутся их начальные значения.) Но если в результате окажется, что искомая масса Δm много меньше начальной массы Земли M₀ (Δm << M₀), то эта оценка вполне разумна и может быть принята в качестве «первого приближения» — как любят говаривать физики.

Далее, чтобы не утруждать себя такими понятиями, как момент силы и момент инерции, Студент смело принял упрощенную модель Земли. Он представил ее в виде обруча, вдоль которого распределена вся ее масса. Тогда начальный «вращательный» импульс Земли равен \(~M_0V_0 = (M_0 - \Delta m)V_0 + \Delta m V_0\) (в этом выражении уже выделена отбрасываемая масса Δm). Сразу после выброса вращение оставшейся массы M₀ - Δm, по предположению, прекратилось, а отброшенная масса приобрела скорость u - V₀ Тогда закон сохранения импульса будет выглядеть так:

\(~(M_0 - \Delta m)V_0 + \Delta m V_0 = (M_0 - \Delta m) \cdot 0 + \Delta m (u - V_0)\) ,

откуда получаем

\(~\frac{\Delta m}{M_0} = \frac{V_0}{u - V_0} = \frac{V_0}{\sqrt{2g_0R_0}}\) .

Осталось найти численные значения. Тут время вспомнить, что радиус Земли R₀ = 6,4·10⁶ м, ее масса M₀ = 6·10⁸ кг, а период обращения вокруг своей оси T₀ = 24 ч. Тогда окружная скорость на экваторе Земли равна

\(~V_0 = \frac{2 \pi R_0}{T_0} = \frac{2 \cdot 3,14 \cdot 6,4 \cdot 10^6}{3600 \cdot 24}\) ≈ 465 м/с.

(больше скорости звука в воздухе!). Стоящее в знаменателе предыдущей формулы выражение \(~\sqrt{2g_0R_0}\) — это вторая космическая скорость υ_II, равная

\(~\upsilon_{II} = \sqrt{2g_0R_0} = \sqrt{2 \cdot 10 \cdot 6,4 \cdot 10^6}\) ≈ 11 км/с.

В итоге получаем

\(~\frac{\Delta m}{M_0} = \frac{0,46}{11} \approx 4%\) .

«А если учесть, что Земля — это не обруч, а шар, — подумал Студент, — то ее затормозить легче, поскольку не вся ее масса находится на расстоянии R₀ от оси вращения». Действительно, неслучайно есть такое понятие, как момент инерции: для шара он равен \(~\frac 25 M_0 R^2_0\), а для обруча \(~M_0 R^2_0\). (Иными словами, Землю можно было бы представить обручем радиусом \(~R = \sqrt{\frac 25} R_0\).) Значит, потребуется выбросить массу еще приблизительно в \(~\frac 25\) раз меньшую, т.е.

\(~\frac{\Delta m}{M_0} < 2%\) .

Именно с такой точностью верно принятое нами предположение Δm << M₀.

Но много это или мало? Сравним, например, с массой земной коры, плавающей на более тяжелой магме (той самой, которая иногда вытекает из вулканов). Земная кора сложена, в основном, из базальтов и гранитов, покрытых менее плотным слоем осадочных пород. Положим для оценок среднюю толщину коры равной h = 20 км, а плотность — порядка ρ = 3·10³ кг/м³. Тогда масса этого шарового слоя будет порядка

\(~m_k = \rho h \cdot 4\pi R^2_0 = 3 \cdot 10^3 \cdot 20 \cdot 10^3 \cdot 4 \pi (6,4 \cdot 10^6)^2\) ≈ 3·10²² кг.

А масса океана еще меньше:

m_ok ≈ 1,4·10²¹ кг.

(Более точные данные можно найти, например, в книге А.В. Бялко «Наша планета — Земля» — М.: Наука, Библиотечка «Квант», вып.29.) В сумме эти массы составляют приблизительно

\(~\frac{3 \cdot 10^{22}}{6 \cdot 10^{24}} = 5 \cdot 10^{-3} = 0,5%\)

от массы Земли. Таким образом, даже если выбросить в космос все океаны и всю земную кору (вплоть до более плотных пород, куда еще никто не добирался), то и этого не хватит, чтобы остановить вращение Земли.

Но пусть даже хватило бы массы. А какую наименьшую энергию надо было бы затратить, чтобы сообщить выбрасываемой массе вторую космическую скорость? Кинетическая энергия этой массы равна

\(~\frac{\Delta m \upsilon^2_{II}}{2} = \frac{0,02 \cdot 6 \cdot 10^{24} \cdot (11 \cdot 10^3)^2}{2}\) ≈ 10³¹ Дж.

Сколько же потребовалось бы, например, керосина, чтобы обеспечить такую потребность в энергии? При сгорании одного килограмма керосина выделяется примерно 4·10⁷ Дж тепла. Если предположить, что все оно идет в «дело» без потерь, то необходимая минимальная масса сгоревшего керосина должна составить

\(~m_{ker} = \frac{10^{31}}{4 \cdot 10^7}\) ≈ 2·10²³ кг.

О, да это ведь сотня океанов из чистого керосина! И Студенту стало жаль и массы, и энергии Земли. «Нет уж, — подумал он, — лучше встать и пойти на лекцию».