Kvant. О законах сохранения

Стасенко А.Л. Рыцарь над пропастью, или Немного о законах сохранения //Квант. — 1998. — № 1. — С. 39-40

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Жил на свете рыцарь бедный,

Молчаливый и простой,

С виду сумрачный и бледный,

Духом смелый и прямой.

А.С.Пушкин

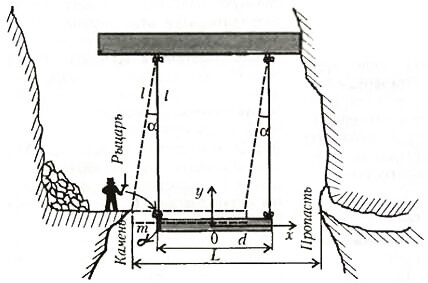
И вот однажды, надев тяжелые боевые доспехи, отправился этот Рыцарь освобождать очередной раз похищенную Принцессу. Вдруг узкая горная тропинка прервалась пропастью, над которой в самой середине висела часть «моста» на нерастяжимых нитях (рис.1). Точнее, это была платформа, до которой ни дотянуться, ни допрыгнуть, да к тому же еще и покрытая тонкой коркой скользкого льда (высокогорье!).

Рис. 1

В крайнем огорчении схватил Рыцарь лежавший на тропе камень массой m и швырнул в мост. Горное эхо двадцать пять раз повторило звук абсолютно упругого удара, а камень низринулся в пропасть. Но — о чудо! — мост начал тихонько качаться. И тут Рыцарь сообразил, что же произошло.

Рис. 2

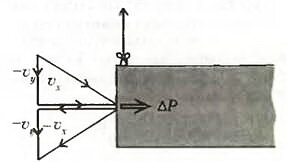
При упругом ударе камня о торец тяжелой платформы и последующем отскоке горизонтальная составляющая импульса камня изменилась на \(~\Delta p = -2m \upsilon_x\) (рис.2). Значит, такое же приращение импульса, но противоположное по знаку, получил и мост:

\(~\Delta P = 2m \upsilon_x\) .

При этом Рыцарь учел для простоты рассуждений — ведь он торопился, — что масса платформы много больше массы камня; а у кого есть время, тот может посчитать точнее, учитывая, что камень отражается от уже начавшей двигаться платформы. Итак, после первого броска платформа получила приращение скорости

\(~\Delta V = \frac{\Delta P}{M}\) .

и стала потихоньку качаться почти без затухания.

Рис. 3

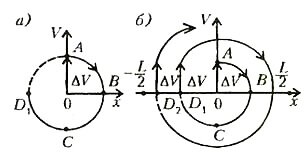
Рыцарь решил изобразить на пыльной тропинке этот процесс. Он нарисовал плоскую систему координат скорость — смещение (V,х). (Позднее эту плоскость назвали фазовой.) До первого удара платформа находилась в начале этой системы координат, в точке 0 (рис.3). В момент удара она получила приращение скорости ΔV (см. вертикальную стрелку и точку А на рисунке а), значит, ей была сообщена начальная кинетическая энергия. И платформа начала двигаться в сторону положительных значений х. Но поскольку тросы, на которых подвешена платформа, нерастяжимы, центр масс платформы движется по окружности и, следовательно, поднимается в поле тяготения. При этом кинетическая энергия переходит в потенциальную, так что в точке B скорость становится равной нулю при максимальном отклонении от положения равновесия. После этого платформа начинает двигаться в сторону Рыцаря, достигая в точке C максимальной скорости, и на мгновение останавливается в точке D₁. Если нет затухания, этот процесс повторяется вечно.

Из рисунка Рыцарю стало ясно, что имеет смысл в точке D₁ бросить еще один камень. При этом, совершив еще одно качание, платформа окажется в точке D₂ (см. рисунок б) — и так будет продолжаться, пока точка D_N не совпадет с координатой \(~x = - \frac L2\). И Рыцарь без колебаний решил оценить, сколько бросков нужно сделать, чтобы край скользкой платформы подошел вплотную к краю пропасти и можно было бы осторожно ступить на платформу.

Он взял свой пыльный щит и написал на нем закон сохранения энергии:

\(~\frac{M V^2_{max}}{2} = Mgl(1 - \cos \alpha)\) .

где V_max — максимальная скорость платформы (очевидно, когда она в своем качании проходит нижнюю точку), а α_max — максимальный угол отклонения, который, как легко видеть из рисунка 1, находится из прямоугольного треугольника:

\(~\cos \alpha = \frac{L - d}{2l}\) .

При этом угле скорость платформы равна нулю: вся кинетическая энергия перешла в потенциальную. Считая, что при каждом ударе камня о платформу (когда она останавливается на мгновение в точке, ближайшей к Рыцарю) последняя получает один и тот же импульс, можно найти требуемое число ударов из условия

\(~V^2_{max} = N \Delta V = N \frac{\Delta P}{M} = N \frac{2m \upsilon_x}{M}\) .

Подставив все это в закон сохранения энергии, Рыцарь получил

\(~\frac 12 \left(\frac{N \cdot 2m \upsilon_x}{M}\right)^2 = gl\left(1 - \frac{L - d}{2l}\right)\) ,

откуда

\(~N = \frac{M}{2m \upsilon_x} \sqrt{g(2l - L + d)}\) .

Теперь нужно сделать численные оценки. Подставив в формулу массу платформы М = 10³ кг, массу камня m = 1 кг, горизонтальную составляющую скорости камня в момент удара υ_x = 10 м/с, ширину пропасти L = 50 м, длину платформы d = 30 м, длину подвеса l = 50 м, он нашел число бросаний камня:

\(~N = 1,4 \cdot 10^3\) .

А сколько времени Рыцарю придется трудиться? Число колебаний платформы известно, осталось узнать их период. Он зависит, конечно, от длины маятника l (м) и от ускорения поля тяготения g (м/с²). Из этих двух величин можно составить единственную формулу, дающую нужную нам размерность периода (с):

\(~\sqrt{\frac lg} \sim T\) .

И Рыцарь вспомнил также, что еще в XV веке дедушка говорил ему: «Помни, что когда речь идет о колебаниях, то, я не знаю почему, всегда появляется 2π».

Итак, период колебаний платформы равен

\(~T = 2\pi \sqrt{\frac lg}\) = 14 с.

Поскольку Т есть одновременно и время между ударами камней, то стало ясно, что трудиться придется не менее чем

\(~t = 14 \cdot 1,4 \cdot 10^3\) с ≈ 2·10⁴ с ≈ 5 ч.

(Хорошо еще, что можно пренебречь затуханием!) Труд не малый, но впереди — Принцесса. И Рыцарь взялся за дело.