Kvant. Планетарная модель атома
Коржуев А. Планетарная модель атома и теория Бора: история, гипотезы, эксперимент //Квант. — 1997. — № 2. — С. 18-20.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Заканчивается XX век. Как он будет назван: веком электроники, авиации, компьютеров? Трудно сказать, но наверняка физики XXI века, оглядываясь в прошлое, назовут его веком квантовой механики, возникновению которой и предшествовали открытия, связанные с «устройством» атома и его закономерностях. О них мы и поговорим.
Немного истории
Начнем со спектроскопии. В 1859 году Г.Кирхгоф и Р.Бунзен разработали метод спектрального анализа и объяснили, в частности, происхождение четырех темных линий поглощения в спектре Солнца. Их обнаружил еще в 1814 году Й.Фраунгофер, а теперь, 45 лет спустя, было показано, что эти линии хорошо совпадают с яркими линиями в спектрах, испускаемых накаленными газами и парами различных веществ в обычных земных условиях. В 1885 году И.Бальмер опубликовал статью, в которой установил, что длины волн этих линий с хорошей точностью подчиняются формуле
где m = 3,4,5 и 6, а k — некоторая постоянная, и могут быть приписаны водороду. Вскоре были обнаружены еще пять линий водорода, но уже в ультрафиолетовой области солнечного спектра поглощения, и их длины волн также с хорошей точностью укладывались в формулу Бальмера. Кстати, эта формула в 1890 году была переписана Ю.Ридбергом для волновых чисел:
Коэффициент \(~\dfrac 4k\) получил название постоянной Ридберга R (по современным данным R = 10973731,77 м-1). Затем обнаружили целых три серии линий в инфракрасной области спектра атома водорода, которые тоже охватывались упомянутой формулой. И вообще, как оказалось, все пять серий линий можно описать одной формулой — формулой Бальмера — Ридберга
где для каждой серии число n свое: n = 1, 2, 3, 4, 5, а внутри серии число m принимает ряд значений, начиная с n + 1. Однако, фундаментального физического обоснования закономерностей линейчатых спектров в то время не было. В частности, существовавшая «пудинговая» модель атома Дж.Дж.Томсона, согласно которой отрицательно заряженные электроны, как изюминки в пудинге, были распределены в неком жидком положительно заряженном веществе, к указанным результатам не приводила.
Теперь следует вспомнить о том, что в 1900 году М.Планку для объяснения закономерностей теплового излучения пришлось выдвинуть идею о квантовой, дискретной структуре излучения и распространения света (уже имевшую, кстати сказать, к моменту рождения «экспериментальное подтверждение» — еще в 1887 году Г. Герц наблюдал внешний фотоэффект), и не забыть о явлениях, также подтверждавших сложное строение атома, — открытии Дж.Дж.Томсоном электрона, обнаружении радиоактивности и термоэлектронной эмиссии.
Что же было общим для всех этих явлений? Очевидно, то, что они не могли быть удовлетворительно объяснены, исходя из существовавших в то время представлений о строении атома. Однако (и история физики это подтверждает) накопление такого рода фактов может происходить достаточно долго, пока не произойдет «скачок» — такое событие в истории науки, которое вынесет окончательный приговор либо в пользу накопившихся фактов, либо в пользу опровергаемой ими теории. Таким «скачком» в истории атома стали опыты Резерфорда, которые легли в основу создания новой теории строения атома.
Опыты Резерфорда
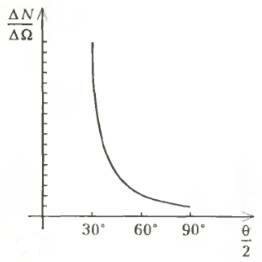
Еще с 1906 года Э.Резерфорд изучал прохождение α-частиц через различные по своим свойствам вещества, а в декабре 1910 года им была выведена формула, описывающая рассеяние α-частиц. Из формулы следовало, что для конкретного источника (с заданными плотностью потока и кинетической энергией частиц) число частиц ΔN, рассеивающихся в телесном угле ΔΩ, связано с углом рассеяния θ соотношением
Соответствующий график изображен на рисунке 1 (коэффициент пропорциональности условно принят за 1).
Помощники Резерфорда (Гейгер и Марсден) провели многие недели в полной темноте, регистрируя вспышки рассеянных фольгой α-частиц на люминесцирующих экранах (они насчитали около двух миллионов различных актов рассеяния). И что же? Оказалось, что некоторые частицы (хотя их относительно мало) отклоняются на очень большие углы — иногда больше 90°, а согласно Томсону такого быть не должно. Полученные данные неопровержимо свидетельствовали о том, что о «пудинге» не может быть и речи. В мае 1911 года Резерфорд впервые опубликовал свои результаты в статье «Рассеяние α-частиц веществом и строение атома», в которой увидела свет ядерная модель атома и обсуждалось ее резкое противоречие модели атома Томсона. Атом по Резерфорду подобен планетарной системе: тяжелое положительно заряженное ядро (Солнце) и вращающиеся по орбитам вокруг него электроны (планеты).
Зададимся, однако, вопросом: был ли Резерфорд одинок в своем отрицании «пудинговой» модели? Неужели никто больше не видел всей сложности противоречий в вопросе о строении атома и не пытался как-то изменить эту модель? История физики свидетельствует: такие попытки были, и были задолго до 1911 года. Например, французский физик Ж.Перрен еще в 1901 году упоминал в своих лекциях о возможности существования ядерно-планетарной структуры атома. А в 1904 году модель сатурноподобного атома предложил японец Х.Нагаока: центральную положительную частицу окружало в его атоме кольцо электронов, двигавшихся с одной и той же угловой скоростью (чем не Сатурн с кольцами?). Неизвестно точно, встречался ли Резерфорд с Нагаокой (который путешествовал примерно в это время по Европе и был даже в Манчестере), но в указанной статье ссылки на эту модель есть. Еще одна, интересная на наш взгляд, аналогичная модель была предложена английским астрофизиком Дж.Никольсоном примерно в 1911 — 1912 годах — он построил ее для объяснения ряда линий непонятного происхождения в спектрах туманностей.
Список можно было бы и продолжить. Однако вернемся к опытам Резерфорда и его статье. Ряд фраз из нее свидетельствовали о том, что сам исследователь не мог не понимать, что его модель противоречит классической электродинамике Максвелла — поскольку ускоренно движущийся заряд должен непрерывно излучать, электрон (в планетарной модели) должен очень быстро упасть на ядро, всего за 10-8 с. Как же тогда может идти речь об устойчивости атома? Да и спектр излучения по классическим представлениям должен быть непрерывным (а не линейчатым), так как частота обращения должна непрерывно меняться. Ядерно-планетарная модель, таким образом, до предела обостряла противоречие теории с наблюдаемой устойчивостью атома. Ситуация возникла драматическая, и самому Резерфорду не было суждено выпутаться из всех противоречий. А выход, тем не менее, был найден.
Гипотеза Бора
Незаурядность Нильса Бора как ученого проявилась довольно рано. В 1905 году, будучи еще студентом Копенгагенского университета, он исследовал колебания струй жидкости с целью измерения коэффициента поверхностного натяжения и был удостоен за работу золотой медали. Магистерскую диссертацию Бор посвятил электронной теории металлов (1909 г.), а затем приступил к докторской диссертации и доказал принципиальную невозможность создания теории магнитных свойств вещества на основе только классических представлений (1911 г.). После защиты диссертации ученый отправляется в Кембридж на годичную стажировку к Дж. Дж.Томсону, где в октябре 1911 года на Кавендишском обеде знакомится с Резерфордом и получает право поработать у него в Манчестерской лаборатории. В это время (весна- осень 1912 г.) Бор и приходит к мысли о том, что из противоречия ядерно-планетарной модели и классической электродинамики придется выбираться с помощью квантовых представлений Планка.
Вернувшись после стажировки в Копенгаген, Бор интенсивно работает и к марту 1913 года готовит три статьи, в которых содержатся основы всей его теории. В сентябре 1913 года Бор выступает с докладом о своих новых результатах в Бирмингеме на заседании Британской ассоциации развития науки. Аудитория — самая авторитетная и взыскательная: корифеи классической физики Рэлей, Джине, Лоренц, Томсон. Доклад был принят патриархами науки весьма прохладно и иронично (лорд Рэлей ограничился лишь замечанием, что людям, которым за 60, уже нет смысла высказывать суждения о новых идеях). Положение изменилось в благоприятную сторону лишь после публикации ряда статей в научных журналах. Первым поддержал Бора Дж.Джине: «Доктор Бор дал в высшей степени остроумное, плодотворное и — я думаю ... — убедительное объяснение закономерностей в спектральных линиях».
Как уже было сказано, к середине второго десятилетия XX века в физике утвердилась идея Планка о дискретном характере энергии атомов, а также идея Эйнштейна о квантовой структуре атома. Что же сделал Бор? Прежде всего он добавил положение о том, что следует отказаться от важнейшего вывода классической электродинамики о непрерывном характере излучения энергии электроном, движущимся вокруг ядра. Взамен были предложены стационарные состояния атома, в которых излучения нет, и возможность перехода между ними либо с излучением, либо с поглощением энергии. Естественно, чтобы решиться на такой шаг, требовалось большое научное мужество. Бор им обладал.
Впоследствии из принятых Бором допущений остались два известных его постулата и правило квантования орбит. Из выражения для энергии электрона, движущегося по орбите,
и уравнения второго закона Ньютона
а также используя идею квантования момента импульса в стационарном состоянии
легко получить знаменитую боровскую формулу для энергии электрона в атоме:
Эта энергия, как видно, представляет собой квантованную величину (принимает дискретный ряд значений, соответствующих целочисленным n = 1, 2, ...). Сам Бор писал об этом так: «Разным n соответствуют ряд значений Wn, соответствующих различным конфигурациям системы, в которых нет излучения, а потому они будут стационарными, пока система не будет возмущена извне».
Интересно, что еще в начале февраля 1913 года по совету одного из коллег Бор сопоставил свой результат с формулой Бальмера - Ридберга для спектра атома водорода (до этого он о ней ничего не знал) и предположил, что так называемые спектральные термы — величины \(~\dfrac{R}{n^2}\) и \(~\dfrac{R}{m^2}\) — пропорциональны энергии электрона в атоме в разных стационарных состояниях. Следующий шаг — предположение о том, что при переходе атома из одного стационарного состояния в другое излучается один квант энергии, откуда и получается знаменитое правило частот (фактически второй постулат Бора)
Совпадение с формулой Бальмера — Ридберга абсолютное, что говорит о хорошем согласии теории с экспериментом. Сохранилось свидетельство известного физика Д.Хевеши о том, что когда об этом блестящем подтверждении теории Бора узнал Эйнштейн, он был потрясен тем фактом, что частота излучения, оказывается, не зависит от частоты вращения электрона в атоме: «Большие глаза Эйнштейна стали еще больше, и он сказал мне: «Тогда это одно из величайших открытий».
Сам же Бор в введении к статье «Связывание электрона положительным ядром» пишет о той большой роли, которую играет в его теории постоянная Планка: «Только существование кванта действия h препятствует слиянию электронов с ядрами в нейтральную частицу практически бесконечно малого размера... Только оно одно дало полное объяснение замечательным зависимостям между физическими и химическими свойствами элементов — зависимостям, выраженным в периодической таблице Менделеева».
Принцип соответствия
Отрицая классическую электродинамику, Бор тем не менее все время пытается найти связь между новой и старой теориями и в 1912 году формулирует свой знаменитый принцип соответствия. Согласно этому принципу, физическая теория, явившаяся обобщением и развитием некоторой классической теории, в ряде предельных случаев должна давать результаты, совпадающие с классическими.
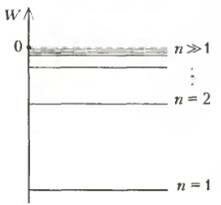
В боровской теории атома это следует понимать так: при больших квантовых числах п выводы теории должны соответствовать классическим представлениям. Для атома водорода, например, при больших квантовых числах «расстояния» между соседними энергетическими уровнями оказываются очень малыми (рис. 2), т.е. уровни становятся квазинепрерывными — это и есть отброшенные классические представления. В работе «О спектре водорода» Бор с помощью этого принципа вычисляет постоянную Ридберга. Попробуйте самостоятельно воспроизвести ход его мыслей.
Теория и эксперимент
Может ли какой-нибудь эксперимент подтвердить результаты теории? Слово А.Эйнштейну: «Опыт никогда не скажет теории «да», но говорит в лучшем случае «может быть», большей частью — просто «нет». Когда опыт согласуется с теорией, для нее это означает «может быть», когда же противоречит ей, объявляется приговор «нет». Таким образом, суждение о том, сколько и каких экспериментов необходимо, чтобы подтвердить истинность теории, не может быть абсолютно безупречным — чем их больше, тем больше у исследователя степень уверенности, что теория достоверна. Но абсолютной уверенности нет никогда — на определенном этапе разработки проблемы может «подвернуться» факт, экспериментальный результат, противоречащий ей, и, если это не случайность, следует серьезно задуматься: всегда ли верна теория (а иногда и о том, верна ли она вообще).
Несмотря на большое число экспериментов, свидетельствовавших в пользу теории Бора, ряд фактов она объяснить не смогла (например, интенсивность спектральных линий, количественный расчет атома гелия, дублетные линии в спектрах и многое другое). В чем же причина? Очевидно, во внутренней противоречивости теории и в попытках соединить несоединимое — классику и квантовые постулаты, и не только в предельных случаях, а во всей области действия.
В 1926-1927 годах Э.Шрёдингер и В.Гейзенберг, опираясь на теорию Бора и многочисленные экспериментальные и теоретические посылки, заложили фундамент последовательной теории строения атома — квантовой механики. А что же теория Бора? Ряд ее результатов, например правила квантования Бора — Зоммерфельда, стали тем предельным случаем, в котором квантовая механика пересеклась с теорией Бора. Некоторые результаты представляют огромный исторический интерес, а идея дискретности микромира — важнейший отправной пункт дальнейших исследований ученых. Теория Бора, по словам Эйнштейна, была «наивысшей музыкальностью в области мысли». Высокую оценку трудов ученого дал и Резерфорд: «Я рассматриваю труды Бора как величайший триумф человеческой мысли».
В 1922 году Бор получил Нобелевскую премию по физике «За заслуги в изучении строения атома».