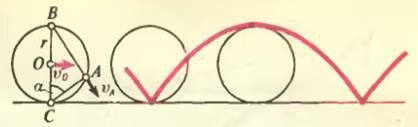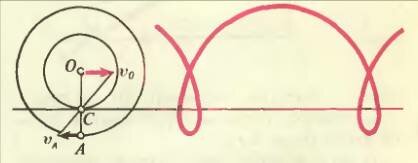Kvant. Плоскопараллельное движение

Фистуль М. Кинематика плоскопараллельного движения //Квант. — 1990. — № 9. — С. 42-44.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Что общего между вращением Земли вокруг своей оси, движением стрелок часов, колес автомобиля на прямолинейном участке пути и т. п.? С точки зрения кинематики, все это примеры так называемого плоскопараллельного движения твердого тела, при котором все точки тела перемещаются в параллельных плоскостях.

Разумеется, в самом общем случае различные точки тела могут двигаться по-разному. Однако принято выделять два частных случая и говорить о двух простейших типах движения — о поступательном движении и о вращении вокруг неподвижной оси. В первом случае все точки тела совершают одинаковые перемещения. Это движение самое простое, и здесь мы его обсуждать не будем. Во втором случае все точки описывают одинаковые траектории — окружности с центрами на оси вращения. Основной характеристикой такого движения является угловая скорость вращения ω.

Давайте вычислим, например, угловые скорости стрелок часов. Так как стрелки вращаются равномерно, то угол поворота φ со временем изменяется по закону φ = ωt (уравнение равномерного вращения). Секундная стрелка делает один оборот за 60 секунд; следовательно, ее угловая скорость равна ω_с = 2π / 60 с = 0,1047 с^-1. Аналогично, скорость часовой стрелки равна ω_ч = 2π / (12·60·60) с = 0,0001455 с^-1.

Рис. 1

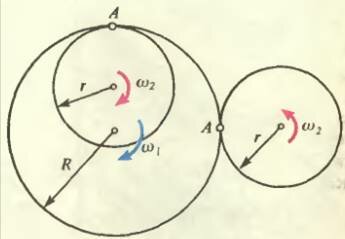
А как добиться того, чтобы секундная и часовая стрелки двигались с различными угловыми скоростями, но синхронно? Оказывается, для этого используется зубчатая передача: два зубчатых колеса могут вращаться вокруг разных осей, но при этом они входят в зацепление друг с другом (рис. 1). Поскольку линейные скорости точки А одинаковы —

\(~\upsilon_A = \omega_1 R = \omega_2 r\) ,

получаем

\(~\frac{\omega_1}{\omega_2} = \frac{r}{R} = \frac{z_1}{z_2}\) ,

где z₁ и z₂ — число зубцов шестеренок.

Кроме того, можно заметить, что при внутреннем зацеплении вращение шестеренок происходит в одном направлении, а при внешнем — в противоположных направлениях. С помощью таких (и более сложных) зубчатых передач осуществляется соединение стрелок в часах, передача усилий в домкрате, изменение величины скорости и «задний ход» у автомобиля.

Теперь рассмотрим более сложное плоскопараллельное движение твердого тела, когда тело вращается, но ось вращения сама поступательно перемещается в пространстве. Скорости такого движения проще всего найти, используя понятие мгновенного центра вращения — так называют точку, скорость которой в данный момент времени равна нулю. Скорости всех остальных точек тела при этом будут такими, как будто тело вращается вокруг неподвижной оси, проходящей через мгновенный центр вращения.

Рис. 2

В качестве примера разберем движение колеса на прямолинейном участке пути без проскальзывания. Так как колесо не проскальзывает, точка С (рис. 2), в которой колесо касается дороги, имеет скорость равную нулю. Значит, точка С и есть мгновенный центр вращения. Найдем, какой будет угловая скорость вращения колеса, если скорость его центра О (скорость поступательного движения колеса) равна υ₀:

\(~\upsilon_0 = \omega r\) , и \(~\omega = {\upsilon_0}{r}\) .

Легко находится и скорость произвольной точки А. Она направлена по линии АВ и равна

\(~\upsilon_A = \omega \cdot CA = 2 \omega r \cos \alpha = 2 \upsilon_0 \cos \alpha\) .

На рисунке 2 изображена также траектория, которую описывает каждая точка обода катящегося колеса. Эта удивительная кривая — циклоида — встретится вам во многих случаях: по такой траектории движутся частицы в «скрещенных» (взаимно перпендикулярных) электрическом и магнитном полях, по циклоиде шарик скатывается за минимальное время и т. д.

Теперь легко ответить на вопрос, который обычно вызывает затруднения: почему, если смотреть на движущегося велосипедиста, то верхние спицы колес сливаются в одно целое, а нижние видны раздельно. Очевидно, это связано с тем, что скорости нижней половины колеса меньше, чем верхней (подумайте, почему, если смотреть на велосипедиста из окна движущегося в ту же сторону автобуса, этот эффект пропадает?).

Рис. 3

А что если мы захотим определить скорость колес вагона движущегося поезда? Мы обнаружим, что на ободе колеса имеются точки, которые движутся назад, в противоположную движению поезда сторону. Это — точки выступающей части колеса, например точка А на рисунке 3. Мгновенный центр вращения (точка С) находится на неподвижном рельсе, по которому колесо катится без проскальзывания. Траектория точки обода колеса еще более любопытна, чем в предыдущем случае,— на траектории имеются возвратные участки движения (петли). Интересно отметить, что аналогичные петлеобразные траектории описывают в своем движении планеты. Их наблюдали еще древнегреческие астрономы, однако объяснить увиденное они не смогли. Сейчас мы знаем, что эти траектории связаны с наложением двух вращений — Земли и наблюдаемой планеты вокруг Солнца.

Всегда ли при плоскопараллельном движении траектории оказываются такими сложными? Попробуйте определить, например, какую траекторию описывают точки обода колеса радиусом r, которое катится по внутренней поверхности неподвижного колеса радиусом 2r.

Рис. 4

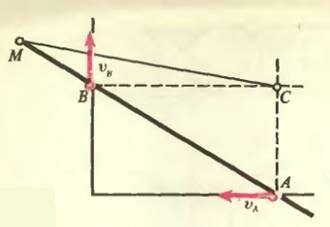
В заключение мы хотим познакомить вас с простым по конструкции, но важным для практики прибором — линейкой-эллипсографом (рис. 4), который служит для вычерчивания эллипсов. Точки А и В такого прибора двигаются по взаимно перпендикулярным направляющим ОА и OB, a точка М при этом описывает эллипс (подумайте, почему). Где находится мгновенный центр вращения в этом случае? Как найти скорость точки М, зная скорости точек А и В?

Рассмотрим жесткий треугольник СВА (точка С лежит на пересечении перпендикуляров к направляющим). Проекции скоростей двух точек твердого тела на линию их соединения всегда равны. Для точек С, А и С, В это возможно, если υ_C, т. е. если точка С — мгновенный центр вращения. Скорость точки М можно определить, зная скорость точки А, например:

\(~\upsilon_A = \omega \cdot CA\) , и \(~\upsilon_M = \upsilon_A \cdot \frac{CM}{CA}\) .

Аналогичным образом, используя понятие мгновенного центра вращения, можно легко находить скорости любых точек механизмов, совершающих плоскопараллельное движение.