Kvant. Правила Кирхгофа

Варламов А.А. Правила Кирхгофа //Квант. — 1985. — № 1. — С. 26-27.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Из учебника «Физика 9» (§ 65) мы узнали о законе Ома для замкнутой цепи, который позволяет находить ток, протекающий в простейшей не- разветвленной электрической цепи, состоящей из источника тока и резистора. Однако на практике чаще приходится иметь дело со сложными, разветвленными цепями типа показанной на рисунке. Они могут содержать несколько источников тока и несколько резисторов. Эти цепи, в свою очередь, могут служить элементами еще более сложной цепи. Для отыскания токов в различных участках таких цепей служат правила Кирхгофа, которые мы и рассмотрим.

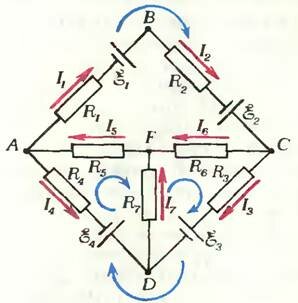
Точки цепи, в которых сходятся три или больше проводов (точки А, В, С, D, F), назовем точками разветвления, или узлами. Ради простоты внутреннее сопротивление каждого источника тока включим в сопротивление резистора в соответствующем участке цепи.

Прежде всего расставим и пронумеруем токи, текущие в каждом участке цепи, произвольно указав их направления. Будем считать ток положительным, если он «втекает» в точку разветвления, и отрицательным в противном случае (о правомерности такого выбора знаков будет сказано ниже). Понятно, что заряд не может ни накапливаться в узле, ни исчезать из него иначе как по подводящим проводам. Следовательно, какой заряд в единицу времени в узел «втекает», такой же заряд должен и «вытечь». Таким образом, мы» пришли к первому правилу Кирхгофа: алгебраическая сумма токов, сходящихся в любой точке разветвления цепи (в узле), равна нулю.

Теперь выделим в нашей сложной схеме какой-либо простой замкнутый контур, например ABCDA, и произвольно выберем направление его обхода — скажем, по часовой стрелке, начиная от точки А. Рассмотрим участок АВ этого контура. Пусть напряжение на нем равно U_AB. В отсутствие источника тока эта величина была бы равна падению напряжения I₁R₁, в резисторе (работа по перемещению заряда из точки А в точку В равна выделяющемуся в резисторе количеству теплоты). Если же на участке есть источник тока, то, в зависимости от его полярности, для переноса заряда из точки А в точку В придется совершить работу, большую или меньшую чем I₁R₁. На данном участке источник тока с ЭДС ε₁, уменьшает разность потенциалов (сторонние силы внутри источника совершают положительную работу), и поэтому можно записать:

\(~U_{AB} = \varphi_A - \varphi_B = I_1 R_1 - \varepsilon_1\) . (1)

На участке ВС все будет точно так же:

\(~U_{BC} = \varphi_B - \varphi_C = I_2 R_2 - \varepsilon_2\) . (2)

В случае же участка CD источник тока имеет противоположную, по сравнению с предыдущими источниками, полярность, и поэтому он не уменьшает, а увеличивает разность потенциалов (сторонние силы внутри источника совершают отрицательную работу):

\(~U_{CD} = \varphi_C - \varphi_D = I_3 R_3 + \varepsilon_3\) . (3)

На последнем участке рассматриваемого контура по нашему предположению ток течет от точки А к точке D, и ситуация полностью соответствует участку АВ:

\(~U_{AD} = I_4 R_4 - \varepsilon_4\) ,

или, учитывая выбранное направление обхода,

\(~U_{DA} = \varphi_D - \varphi_A = U_{AD} = -I_4 R_4 + \varepsilon_4\) . (4)

Складывая почленно равенства (1)—(4), получаем:

\(~I_1 R_1 + I_2 R_2 + I_3 R_3 - I_4 R_4 = \varepsilon_1 + \varepsilon_2 - \varepsilon_3 - \varepsilon_4\) .

Это соотношение выражает второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС.

Правила Кирхгофа не выражают никаких новых свойств электрического поля и поэтому не могут рассматриваться как физические законы. Первое из них, как мы уже говорили, есть следствие закона сохранения заряда, второе — следствие закона сохранения энергии. Однако они оказываются чрезвычайно полезными при отыскании токов в разветвленных цепях.

Вернемся к схеме, изображенной на рисунке, и запишем уравнения, выражающие правила Кирхгофа для узлов А, В, С, F и контуров ABCDA, AFDA, DFCD:

\(~\begin{matrix} I_5 - I_1 - I_4 = 0, \\ I_1 - I_2 = 0, \\ I_2 - I_3 - I_6 = 0, \\ I_6 + I_7 - I_5 = 0, \\ I_1 R_1 + I_2 R_2 + I_3 R_3 - I_4 R_4 = \varepsilon_1 + \varepsilon_2 - \varepsilon_3 - \varepsilon_4, \\ -I_4 R_4 - I_5 R_5 - I_7 R_7 = -\varepsilon_4, \\ I_7 R_7 - I_6 R_6 + I_3 R_3 = -\varepsilon_3. \end{matrix}\)

Еще раз обратим внимание на выбор знаков «плюс» или «минус» при составлении уравнений. Перед падением напряжения на резисторе ставится знак «плюс», если выбранное нами направление тока на этом участке совпадает с выбранным направлением обхода, и знак «минус» — в противном случае. ЭДС источника берется со знаком «плюс», если направление тока, который он мог бы создать в контуре, совпадает с направлением обхода контура, и со знаком «минус» — в противоположном случае.

Истинное же направление токов можно определить лишь после решения системы уравнений: если полученное значение какого-либо тока окажется положительным, то это значит, что направление этого тока было выбрано верно; если же ток получится отрицательным, значит, его истинное направление противоположно выбранному.

Нетрудно показать, что, применяя правила Кирхгофа, всегда можно получить ровно столько независимых уравнений, сколько неизвестных токов, то есть полностью и однозначно решить поставленную задачу.