Kvant. Работа сил трения
Мякишев Г.Я., Кондрашева Л., Крюков С. Работа сил трения //Квант. — 1991. — № 5. — С. 37-39.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Сила трения, как и любая другая сила, совершает работу и соответственно изменяет кинетическую энергию тела при условии, если точка приложения силы перемещается в выбранной системе отсчета. Однако сила трения существенно отличается от других, так называемых консервативных, сил (тяготения и упругости), так как ее работа зависит от формы траектории. Вот почему работу сил трения ни при каких обстоятельствах нельзя представить в виде изменения потенциальной энергии системы. Кроме того, дополнительные сложности при вычислении работы создает специфика силы трения покоя. Здесь существует ряд стереотипов физического мышления, которые хотя и лишены смысла, но очень устойчивы.
Мы рассмотрим несколько вопросов, связанных с не вполне правильным пониманием роли силы трения в изменении энергии системы тел.
О силе трения скольжения
Нередко говорят, что сила трения скольжения всегда совершает отрицательную работу и это приводит к увеличению внутренней (тепловой) энергии системы.
Такое утверждение нуждается в важном уточнении — оно справедливо только в том случае, если речь идет не о работе одной отдельно взятой силы трения скольжения, а о суммарной работе всех таких сил, действующих в системе. Дело в том, что работа любой силы зависит от выбора системы отсчета и может быть отрицательной в одной системе, но положительной в другой. Суммарная же работа всех сил трения, действующих в системе, не зависит от выбора системы отсчета и всегда отрицательна. Вот конкретный пример.
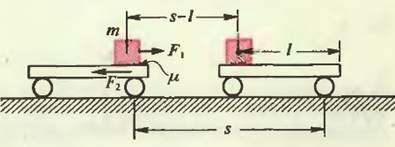
Положим кирпич на движущуюся тележку так, чтобы он начал по ней скользить (рис. 1). В системе отсчета, связанной с землей, сила трения F1, действующая на кирпич до, прекращения скольжения, совершает положительную работу A1. Одновременно сила трения F2, действующая на тележку (и равная по модулю первой силе), совершает отрицательную работу A2, по модулю большую, чем работа A1, так как путь тележки s больше пути кирпича s - l (l — путь кирпича относительно тележки). Таким образом, получаем
и полная работа сил трения
Поэтому кинетическая энергия системы убывает (переходит в тепло):
Этот вывод имеет общее значение. Действительно, работа двух сил (не только сил трения), осуществляющих взаимодействие между телами, не зависит от выбора системы отсчета (докажите это самостоятельно). Всегда можно перейти к системе отсчета, относительно которой одно из тел покоится. В ней работа силы трения, действующей на движущееся тело, всегда отрицательна, так как сила трения направлена против относительной скорости. Но она отрицательна и в любой другой системе отсчета. Следовательно, всегда, при любом количестве тел в системе, Atr < 0. Эта работа и уменьшает механическую энергию системы.
О силе трения покоя
При действии между соприкасающимися телами силы трения покоя ни механическая, ни внутренняя (тепловая) энергия этих тел не изменяется. Значит ли это, что работа силы трения покоя равна нулю? Как и в первом случае, такое утверждение правильно только по отношению к полной работе сил трения покоя над всеми взаимодействующими телами. Одна же отдельно взятая сила трения покоя может совершать работу, причем как отрицательную, так и положительную.
Рассмотрим, например, книгу, лежащую на столе в набирающем скорость поезде. Именно сила трения покоя сообщает книге такую же скорость, как у поезда, т. е. увеличивает ее кинетическую энергию, совершая определенную работу при этом. Другое дело, что такая же по модулю, но противоположная по направлению сила действует со стороны книги на стол, а значит, и на поезд в целом. Эта сила совершает точно такую же работу, но только отрицательную. В результате получается, что полная работа двух сил трения покоя равна нулю, и механическая энергия системы тел не меняется.
О движении автомобиля без проскальзывания колес
Самое устойчивое заблуждение связано именно с этим вопросом.
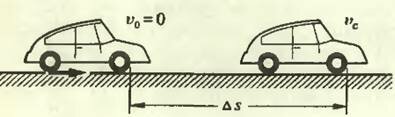
Пусть автомобиль вначале покоится, а затем начинает разгоняться (рис. 2). Единственной внешней силой, сообщающей автомобилю ускорение, является сила трения покоя Ftr действующая на ведущие колеса (мы пренебрегаем силой сопротивления воздуха и силой трения качения). Согласно теореме о движении центра масс, импульс силы трения равен изменению импульса автомобиля:
если скорость центра масс в начале движения равнялась нулю, а в конце υc. Приобретая импульс, т. е. увеличивая свою скорость, автомобиль одновременно получает и определенную порцию кинетической энергии. А поскольку импульс сообщается силой трения, естественно считать, что и увеличение кинетической энергии определяется работой этой же силы. Вот это-то утверждение оказывается совершенно неверным. Сила трения ускоряет автомобиль, но работы при этом не совершает. Как же так?
Вообще говоря, ничего парадоксального в этой ситуации нет. В качестве примера достаточно рассмотреть совсем простую модель — гладкий кубик с прикрепленной сбоку пружинкой (рис. 3). Кубик, придвигают к стене, сжимая пружинку, а затем отпускают. «Отталкиваясь» от стены, наша система (кубик с пружинкой) приобретает определенные импульс и кинетическую энергию. Единственной внешней силой, действующей по горизонтали на систему, является, очевидно, сила реакции стены Fp. Именно она и сообщает системе ускорение. Однако никакой работы при этом, конечно, не совершается — ведь точка приложения этой силы неподвижна (в системе координат, связанной с землей), хотя сила действует некоторое конечное время Δt.
Аналогичная ситуация возникает и при разгоне автомобиля без проскальзывания. Точка приложения силы трения, действующей на ведущее колесо автомобиля, т. е. точка соприкосновения колеса с дорогой, в любой момент покоится относительно дороги (в системе отсчета, связанной с дорогой). При движении автомобиля она исчезает в одной точке и сразу же появляется в соседней.
Не противоречит ли сказанное закону сохранения механической энергии? Конечно же, нет. В нашем случае с автомобилем изменение кинетической энергии системы происходит за счет ее внутренней энергии, выделяющейся при сгорании топлива.
Для простоты рассмотрим чисто механическую систему: игрушечный автомобиль с пружинным заводом. Двигатель такого автомобиля использует не внутреннюю энергию топлива, а потенциальную энергию сжатой пружины. Вначале пружина заведена, и ее потенциальная энергия Ep1 отлична от нуля. Если двигатель игрушки — просто растянутая пружина, то \(~E_{p1} = \frac{k (\Delta l)^2}{2}\). Кинетическая энергия равна нулю, и полная начальная энергия автомобиля E1 = Ep1. В конечном состоянии, когда деформация пружины исчезнет, потенциальная энергия равна нулю, а кинетическая энергия \(~E_{k2} = \frac{M \upsilon_c^2}{2}\). Полная энергия E2 = Ek2. Согласно закону сохранения энергии (трением мы пренебрегаем),
В случае реального автомобиля
где ΔU — энергия, полученная при сгорании топлива.
Если колеса автомобиля проскальзывают, то Atr<0, так как точка соприкосновения колес с дорогой движется против направления силы трения. Следовательно,
Видно, что кинетическая энергия автомобиля в конечном состоянии оказывается меньше, чем в отсутствие проскальзывания.