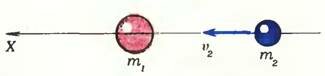Kvant. Столкновения тел

Асламазов Л.Г. Столкновения тел //Квант. — 1984. — № 4. — С. 23-24.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

В учебнике «Физика 8» сказано, что законы сохранения позволяют решать некоторые задачи механики даже тогда, когда не известны действующие на тело силы. К такому случаю относится, например, задача об упругом столкновении шаров.

Рис. 1

Для простоты мы рассмотрим удар двух шаров с массами m₁ и m₂, из которых первоначально один покоится (υ₁ = 0), а второй движется по направлению к первому со скоростью \(~\vec \upsilon_2\) (рис. 1). При столкновении происходит так называемый центральный (или лобовой) упругий удар. Каковы скорости обоих шаров после столкновения?

Чтобы ответить на этот вопрос, попытаемся воспользоваться законами сохранения энергии и импульса, о которых рассказывается в «Физике 8». Начнем с импульса.

До столкновения импульс первого шара равен нулю, а импульс второго равен \(~m_2 \vec \upsilon_2\). Следовательно, общий импульс двух шаров был равен \(~m_2 \vec \upsilon_2\). После столкновения импульсы обоих шаров изменились и стали равными \(~m_1 \vec u_1\) и \(~m_2 \vec u_2\) соответственно. Общий импульс теперь равен \(~m_1 \vec u_1 + m_2 \vec u_2\).

По закону сохранения импульса общий импульс шаров (можно считать, что они образуют замкнутую систему тел) измениться не может. Поэтому мы должны написать

\(~m_2 \vec \upsilon_2 = m_1 \vec u_1 + m_2 \vec u_2\) .

Геометрическое сложение импульсов можно заменить алгебраическим сложением их проекций. Направим координатную ось вдоль линии, соединяющей центры шаров, в направлении скорости \(~\vec \upsilon_2\). Тогда для проекций импульсов на эту ось имеем

\(~m_2 \upsilon_{2x} = m_1 u_{1x} + m_2 u_{2x}\) .

При выбранном направлении оси

\(~\upsilon_{2x} = \upsilon_2, |u_{1x}| = u_1, |u_{2x}| = u_2\) ,

но знаки проекций u_1x и u_2x могут быть как положительными, так и отрицательными.

Из одного этого равенства мы, конечно, не можем найти две неизвестные проекции скоростей u_1x и u_2x. Необходимо еще одно уравнение.

Рис. 2

Будем считать, что сила взаимодействия F шаров при столкновении (рис. 2) — сила упругости (именно в таком случае удар называют упругим). Тогда справедлив закон сохранения механической энергии

\(~\frac{m_2 \upsilon^2_2}{2} = \frac{m_1 u^2_1}{2} + \frac{m_2 u^2_2}{2}\) ,

ИЛИ

\(~\frac{m_2 \upsilon^2_2}{2} = \frac{m_1 u^2_{1x}}{2} + \frac{m_2 u^2_{2x}}{2}\) .

Теперь мы имеем систему двух уравнении

\(~\left\{\begin{matrix} m_2 \upsilon_{2x} = m_1 u_{1x} + m_2 u_{2x} \\ \frac{m_2 \upsilon^2_2}{2} = \frac{m_1 u^2_{1x}}{2} + \frac{m_2 u^2_{2x}}{2} \end{matrix}\right.\)

из которой можно найти проекции u_1x и u_2x скоростей шаров после столкновения. Предлагаем читателям самостоятельно решить эту систему и показать, что первый, покоившийся до столкновения шар получит скорость, проекция которой

\(~u_{1x} = \frac{2 m_2 \upsilon_2}{m_1 + m_2}\) ,

а проекция второго шара

\(~u_{2x} = \frac{m_2 - m_1}{m_1 + m_2} \upsilon_2\) .

Рис. 3

Легко видеть, что проекция скорости первого шара всегда положительная, а проекция второго может быть как положительной, так и отрицательной. Если масса налетающего шара меньше массы покоящегося (m₂ < m₁), то u_2x отрицательна. Это означает, что шар после столкновения изменяет направление своей скорости (отскакивает от покоившегося шара, как показано на рисунке 3). При обратном соотношении масс (m₂ > m₁) проекция u_2x > 0, и направление движения налетающего шара после столкновения не меняется (отскакивает покоившийся шар). Если же массы обоих шаров равны (m₁ = m₂), то u_1x = υ₂, а u_2x = 0. Это значит, что второй шар, столкнувшись с первым, передал ему свой импульс, а сам остановился.

Таким образом, пользуясь законами сохранения энергии и импульса, можно, зная скорости тел до столкновения, определить их скорости после столкновения. А как обстояло дело во время столкновения, когда шары уже соприкоснулись друг с другом, но еще не разошлись?

При столкновении шары деформируются. Сначала их деформация растет, затем уменьшается. В момент наибольшей деформации шары движутся вместе с одной и той же скоростью. Рассмотрим этот момент подробнее. Обозначим скорость их совместного движения через \(~\vec u\) и будем считать, для простоты, массы шаров одинаковыми (m₁ = m₂ = m). По закону сохранения импульса

\(~m \vec \upsilon_2 = 2 m u_x\) .

Отсюда следует, что \(~u_x = u = \frac{\upsilon_2}{2}\). Таким образом, скорость обоих шаров при их совместном движении равна половине скорости одного из них до столкновения.

Что касается кинетической энергии шаров, то в момент их движения с одной и той же скоростью она равна \(~2 \frac{mu^2}{2} = mu^2 = \frac{m \upsilon^2_2}{4}\). А до столкновения общая энергия шаров была равна \(~\frac{m \upsilon^2_2}{2}\). Следовательно, кинетическая энергия, уменьшилась вдвое. Куда же она исчезла? Не происходит ли здесь нарушения закона сохранения энергии, как это может показаться на первый взгляд?

Энергия, конечно же, осталась прежней. Все дело в том, что во время столкновения оба шара были деформированы, и поэтому они обладали потенциальной энергией упругого взаимодействия. Именно на величину этой потенциальной энергии и уменьшилась кинетическая энергия шаров. Вначале, когда деформация росла, потенциальная энергия увеличивалась и в момент совместного движения шаров она достигла своего максимального значения (в нашем случае равного половине общего запаса энергии). Затем деформация уменьшилась, а запасенная потенциальная энергия перешла обратно в кинетическую.