Kvant. Стрельба

Стасенко А.Л. Не стреляйте в белых лебедей //Квант. — 1998. — № 5. — С. 34-35.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Известно, что на тело, движущееся в воздухе, действует сила сопротивления \(~\vec F\). Почти очевидно, что эта сила зависит от скорости движения \(~\vec \upsilon\) и размеров тела, например площади поперечного сечения S, причем эта зависимость типа «чем больше υ и S, тем больше F». Можно еще уточнить вид этой зависимости, исходя из соображений размерностей (единиц измерения). Действительно, сила измеряется в ньютонах ([F] = Н), а Н = кг·м/с². Видно, что секунда в квадрате входит в знаменатель. Отсюда сразу ясно, что сила должна быть пропорциональна квадрату скорости тела ([υ²] = м²/с²) и плотности ([ρ] = кг/м³) - конечно, той среды, в которой движется тело. Итак,

\(~F \sim \rho S \upsilon^2\) .

А чтобы подчеркнуть, что эта сила направлена против вектора скорости, можно записать так:

\(~\vec F \sim -\rho S \upsilon \vec \upsilon\) .

Мы узнали уже очень много, но это еще не все. Наверняка сила сопротивления (аэродинамическая сила) зависит и от формы тела - не случайно ведь летательные аппараты делаются «хорошо обтекаемыми». Чтобы учесть и эту предполагаемую зависимость, можно в полученное выше соотношение (пропорциональность) ввести безразмерный множитель, который не нарушит равенства размерностей в обеих частях этого соотношения, но превратит его в равенство:

\(~\vec F = - \alpha \rho S \upsilon \vec \upsilon\) .

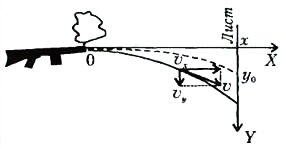
Представим себе шарик, движущийся в воздухе, - например дробинку, горизонтально вылетевшую с начальной скоростью \(~\vec \upsilon_0\) - Если бы не было сопротивления воздуха (в школьных задачах обычно так и говорится: «сопротивлением воздуха пренебречь»), то на расстоянии х за время \(~t_0 = \frac{x}{\upsilon_0}\) дробинка сместилась бы по вертикали вниз на

\(~y_0 = \frac{gt^2_0}{2} = \frac g2 \left( \frac{x}{\upsilon_0} \right)^2\) . (1)

Соответствующая кривая (парабола) изображена на рисунке 1 штриховой линией (заметим, что ось Y направлена вниз). Но из-за действия силы сопротивления (направленной против вектора скорости) время полета дробинки до вертикальной плоскости х будет больше t₀. Следовательно, сила тяжести \(~m \vec g\) дольше будет действовать на дробинку, так что она опустится ниже y₀.

Рис. 1

И вообще, дробинка будет двигаться по другой кривой (сплошная линия на рисунке 1), уже не являющейся параболой (ее называют баллистической траекторией).

И тут наше успешное продвижение в познании силы сопротивления резко замедляется. Соображения размерности уже бесполезны: ведь α - безразмерный множитель. Чтобы узнать его для тела конкретной формы, нужны либо численные решения уравнений газодинамики (описывающих движение воздуха вокруг этого тела), либо экспериментальные исследования (есть наука, которая так и называется: экспериментальная аэрогазодинамика).

Что можно сказать об этой кривой? Если были бы известны начальная скорость дробинки υ₀ и коэффициент α в силе сопротивления, то нужно было бы написать уравнение второго закона Ньютона и решить его. Это - дело математики, но кто даст математикам эти величины? Попробуем справиться сами.

Примем такой план действий:

1. Постараемся как можно подробнее (при наших скромных математических знаниях) описать движение дробинки для любых значений α и υ₀.
2. Экспериментально измерим вертикальные смещения дробинки, например, при помощи вертикального листа бумаги, помещенного на известном расстоянии х от ружья.
3. Сравнивая теорию и эксперимент, получим α и υ₀.

Итак, прежде всего запишем уравнение движения дробинки под действием силы тяжести \(~m \vec g\) и силы сопротивления воздуха \(~\vec F\), определенной выше:

\(~m \vec a = m \vec g - \alpha \rho S \upsilon \vec \upsilon\) .

Разделим обе части этого уравнения на массу дробинки m. Очевидно, что тогда последнее слагаемое будет обратно пропорционально радиусу дробинки: действительно, площадь поперечного сечения шарика пропорциональна квадрату радиуса, а объем (и, значит, масса) - кубу радиуса. Если считать, что α не зависит от размеров шарика, то эту величину и плотность воздуха можно «спрятать» в новую постоянную β, так что получим

\(~\vec a = \vec g - \frac{\beta}{r} \upsilon \vec \upsilon\) . (2)

Заметим, что в отсутствие сопротивления (когда α и β равны нулю) траектории всех дробинок одинаковы и все они попадут в точку y₀. А вот сопротивление воздуха как раз и позволяет «рассортировать» их по размерам. (Это же «сортирующее свойство» используется в сельском хозяйстве, на току, когда боковой ветер отделяет легкую шелуху от полновесных зерен.) Из уравнения (2) видно, что чем меньше дробинка, тем сильнее влияет на ее движение воздух (радиус входит в знаменатель). И наоборот, чем массивнее тело, тем с большей точностью можно пренебречь сопротивлением, так что останется только сила тяжести (\(~\vec a_0 = \vec g\)). Только в этом предельном случае и верен вывод из экспериментов Галилея, бросавшего пушечные ядра и мушкетные пули с башни: «скорость падающих тел одинакова, независимо от их веса». Но мы здесь как раз и хотим использовать «сортирующее свойство» силы сопротивления воздуха. Поэтому подробнее исследуем уравнение (2).

Модуль скорости связан с горизонтальной и вертикальной составляющими соотношением \(~\upsilon = \sqrt{\upsilon^2_x + \upsilon^2_y}\) . И тут сделаем первое упрощающее предположение. Интуитивно ясно, что вначале скорость вертикального падения дробинки много меньше скорости горизонтального движения (если не очень удаляться от ружья), а уж их квадраты и подавно сильно отличаются друг от друга. Значит, можно приближенно считать, что υ ≈ υ_x.

Теперь сделаем второе упрощающее предположение. Будем считать, что сила сопротивления воздуха при вертикальном перемещении дробинки мала по сравнению с силой тяжести (в начальный момент времени она вообше равна нулю). Можно короче сформулировать это предположение так: будем считать, что дробинка перемещается в горизонтальном направлении с большой скоростью и заметно тормозится при этом (ведь сила сопротивления пропорциональна квадрату скорости), а в вертикальном направлении она перемещается как свободно падающее (без сопротивления) тело по тому же закону (1):

\(~y = \frac{gt^2}{2} = \frac g2 \left( \frac{x}{\upsilon_{x\ cp}} \right)^2\) , (3)

в который, однако, входит средняя горизонтальная скорость υ_{x cp} на отрезке, Ox.

В этих предположениях уравнение (2) для горизонтального и вертикального движений примет вид

\(~\begin{matrix} a_x = - \frac{\beta}{r} \upsilon^2_x \\ a_y = g \end{matrix}\) . (4)

Решение второго уравнения уже найдено: это равноускоренное падение (3). Рассмотрим первое уравнение. Ускорение равно отношению изменения скорости Δυ_x ко времени Δt, которое, в свою очередь, можно выразить через скорость υ_x, а именно\[~\Delta t = \frac{\Delta x}{\upsilon_x}\]. Итак,

\(~a_x = \frac{\Delta \upsilon_x}{\Delta t} = \upsilon_x \frac{\Delta \upsilon_x}{\Delta x}\) ,

и тогда первое уравнение можно сократить на υ_x и получить

\(~\Delta \upsilon_x = - \frac{\beta}{r} \upsilon_x \Delta x\) . (5)

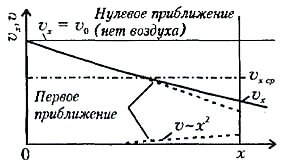
Это так называемое релаксационное уравнение: изменение искомой величины (в данном случае - горизонтальной составляющей скорости) пропорционально самой величине. И решение этого уравнения известно - это экспонента. Но чтобы не пугать себя словами, посмотрим на рисунок 2 и заметим, что на начальном участке изменение величины υ_x очень похоже на прямую (пунктир).

Рис. 2

Попробуем оценить изменение горизонтальной скорости, не решая уравнение (5) точно. Когда физики не могут (или не хотят) решать точно, они применяют метод последовательных приближений. Он «работает» так.

Если пренебречь сопротивлением воздуха, то решение известно: υ_x = υ₀ - горизонтальная составляющая скорости не изменяется. Подставим это так называемое нулевое приближение в уравнение (5):,

\(~\Delta \upsilon_x \approx - \frac{\beta}{r} \upsilon_0 \Delta x\)

и получим уравнение для первого приближения. Видно, что в этом приближении скорость линейно уменьшается со временем:

\(~\upsilon_x = \upsilon_0 \left(1 - \frac{\beta}{r} x \right)\) . (6)

Это и есть пунктирная прямая на рисунке 2. Средняя скорость на участке Ox в этом приближении равна (штрих-пунктир на рисунке)

\(~\upsilon_{x\ cp} = \upsilon_0 \left(1 - \frac{\beta}{2r} x \right)\) .

Подставив это значение в (3), найдем уравнение баллистической кривой в первом приближении:

\(~y = \frac{gx^2}{2 \upsilon_0} \frac{1}{1 - \frac{\beta}{2r} x}\) .

Предположим, что из ружья вылетели две дробинки радиусами r₁ и r₂, которые пробили вертикальный лист бумаги, расположенный на расстоянии х = l, в точках y₁ и y₂. Тогда из последнего соотношения получим два уравнения с двумя неизвестными, из которых найдем и начальную скорость вылета, и коэффициент сопротивления дробинок:

\(~\upsilon_0 = l \sqrt{\frac{g}{2y_1}} \frac{1}{1 - \frac{1 - \sqrt{\frac{y_1}{y_2}}}{r_1 \left( \frac{1}{r_2} - \frac{\sqrt{\frac{y_1}{y_2}}}{r_1} \right)}}\) , \(~\beta = \frac{1 - \sqrt{\frac{y_1}{y_2}}}{\frac l2 \left( \frac{1}{r_2} - \frac{\sqrt{\frac{y_1}{y_2}}}{r_1} \right)}\) .

Можно ограничиться этим приближением, а можно пойти дальше. Подставив первое приближение (6) в правую часть уравнения (5), найдем второе приближение для скорости, и так далее. Все эти приближения сойдутся (как говорят математики) к точному решению для баллистической кривой:

\(~y = \frac g2 \left(\frac{x}{\upsilon_0}\right)^2 \left(\frac{r}{2 \beta x} e^{\frac{2 \beta x}{r}} - \frac 1x \right)\) ,

где первый сомножитель есть y₀(х) (см. (1)).

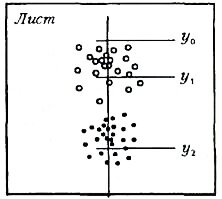
И тут пора начать сомневаться. Ведь даже если эти две дробинки выталкиваются одним пыжом - все равно они могут приобрести какие-то начальные вертикальные скорости. А если взять не две дробинки, а много дробинок двух сортов (с теми же радиусами r₁ и r₂), то они в процессе движения могут сталкиваться друг с другом или взаимодействовать через те возмущения, которые они производят в воздухе. И сами дробинки могут быть не строго шаровыми, что приведет к появлению «подъемной» силы (вверх или вниз) или боковых сил, или к вращению дробинок, или... И тогда мы получим на листе бумаги разброс точек, качественно показанный на рисунке 3, в котором y₁ и y₂ — это «центры тяжести» точек попадания частиц двух сортов. И, значит, траектория дробинки приобретет вероятностный смысл, а в обработке эксперимента придется использовать теорию ошибок. И тогда ...

Рис. 3

Но это уже предмет будущих исследований наших читателей.