Kvant. Траектория, путь

Кикоин А.К. Траектория, путь, перемещение //Квант. — 1984. — № 9. — С. 19-20.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Три слова в заглавии этой заметки связаны с движением тел (материальных точек). Первые два широко употребляются в житейском обиходе, третьим пользуются, главным образом, в науке о движении тел — механике.

Траектория — это непрерывная линия, которую описывает движущаяся точка. Она может быть прямой линией. Отеле (точке), движущемся по такой траектории, говорят, что оно совершает прямолинейное движение. Траектория может представлять собой и кривую линию любой формы. Тело, движущееся по такой траектории, совершает криволинейное движение. Например, траектория свободно падающего тела по отношению к Земле (если пренебречь ее вращением) — вертикальная прямая, а траектория искусственного спутника Земли — кривая (окружность или эллипс).

Если траектория известна заранее, то задачей механики может быть, скажем, определение точки на траектории, где находится движущееся тело в тот или иной момент времени. Траектория может быть и неизвестной, тогда задача состоит в том, чтобы найти вид траектории. Законы движения позволяют решать и ту, и другую задачи.

Путь, пройденный телом (точкой),— это длина его траектории (измеренная в метрах, километрах и т. д.). Его можно определить, например, по счетчику километров в автомобиле.

Для решения задач механики знать пройденный путь обычно недостаточно и вот почему. Явление движения тела состоит в том, что с течением времени изменяются координаты тела. Путь же с изменением координат связан не всегда. Может даже случиться и так, что пройденный путь не равен нулю, а изменение координат равно нулю (тело прошло по замкнутой траектории). Вот поэтому путь, как правило, в уравнения механики не входит.

Для описания движения тела (точки) в механике (точнее — в кинематике) используется другая физическая величина — перемещение. Напомним, что перемещение — это направленный отрезок прямой (вектор), соединяющий некоторое начальное положение движущейся точки с каким-то последующим ее положением («Физика 8», §3). Важность для механики именно этой величины вытекает из того, что проекции вектора перемещения на оси координат равны изменениям соответствующих координат («Физика 8», §5). А это значит, что, если известен вектор перемещения, можно найти и координаты тела. Правда, для этого нужно знать еще начальные координаты.

Рис. 1

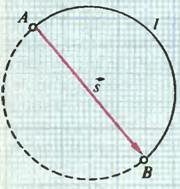
Возникает вопрос: не равны ли друг другу модуль вектора перемещения и пройденный путь (и то и другое — скаляры)? Оказывается, что в общем случае — нет, не равны. Например, если тело из точки А пришло в точку В по траектории, представляющей собой половину окружности радиуса R, то пройденный телом путь l = πR, а модуль перемещения \(~|\vec s| = 2R\) (рис. 1). Если бы тело прошло не половину окружности, а сделало полный оборот (вторая половина траектории показана на рисунке 1 штриховой линией), то путь был бы равен 2πR, а модуль перемещения — нулю. Только в одном случае, когда траектория движения тела — прямая линия и тело движется по такой траектории в одном направлении, модуль перемещения и пройденный путь равны друг другу.

Рис. 2

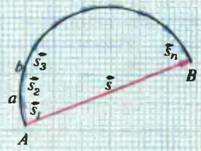
Существует простая связь между величинами перемещения и пройденного пути. Поясним ее на уже рассмотренном примере движения тела по полуокружности. Разобьем эту траекторию на малые участки 1, 2, 3 и т. д. (рис. 2). На участке 1 путь тела — это длина дуги Аа, а перемещение \(~\vec s_1\) по модулю равно длине хорды Аа. На участке 2 путь тела — это длина дуги ab, а модуль перемещения \(~\vec s_2\) — длина хорды ab и т. д. Можно сделать участки, на которые мы разбили траекторию, такими малыми, чтобы дуга участка мало отличалась от хорды. Тогда, как это видно из рисунка 2, вектор полного перемещения \(~\vec s\) равен сумме векторов элементарных перемещений \(~\vec s_1\), \(~\vec s_2\), \(~\vec s_3\) и т. д.:

\(~\vec s = \vec s_1 + \vec s_2 + \vec s_3 + \ldots + \vec s_n\) ,

а длина пути l равна алгебраической сумме модулей \(~|\vec s_1|\), \(~|\vec s_2|\), \(~|\vec s_3|\) и т. д. элементарных перемещений:

\(~l = |\vec s_1| + |\vec s_2| + |\vec s_3| + \ldots + |\vec s_n|\) .