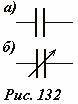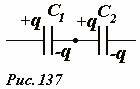Слободянюк А.И. Физика 10/16.1

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

В многочисленных электротехнических устройствах происходят постоянные переходы энергии из одной формы в другую. В данном параграфе мы рассмотрим некоторые примеры таких превращений и покажем, что во многих случаях эти переходы связаны с преобразованиями электрических и магнитных полей. Начнем обсуждение этих проблем с устройств, способных накапливать электрический заряд, сохранять его и создаваемое ими электрическое поле в течение длительного промежутка времени.

16.1 Электроемкость.

16.1.1 Электроемкость уединенного проводника.

Любое тело способно накапливать электрический заряд. На первый взгляд, кажется, что любому телу можно сообщить сколь угодно большой заряд. Однако существует ряд причин, которые ограничивают величину максимального заряда. С ростом электрического заряда возрастает напряженность поля, создаваемого телом. Если тело находится в воздухе или другой среде, то может начаться электрический разряд, посредством которого заряд начнет стекать с тела. Даже если рассматриваемое тело находится в вакууме, то электростатическое взаимодействие заряженных частиц внутри вещества приведет к испусканию, эмиссии частиц (чаще всего электронов), что тоже приведет к уменьшению заряда тела. Поэтому необходимо ввести некоторую характеристику тела, описывающую его возможность накапливать электрический заряд. Такой характеристикой является электроемкость тела C : отношение заряда тела к его потенциалу

\(~C = \frac{Q}{\varphi}\) . (1)

В этом определении необходимо оговорить, относительно какой точки определяется потенциал. Как правило, для уединенного тела его потенциал отсчитывается относительно бесконечности. Можно дать и несколько иное определение, свободное от указанной неопределенности значения потенциала: электроемкость тела равна заряду, который необходимо сообщить телу, чтобы увеличить его потенциал на единицу

\(~C = \frac{\Delta Q}{\Delta \varphi}\) . (2)

Вспомним другую «емкость»: теплоемкость тела равна количеству теплоты, которое необходимо сообщить телу, чтобы увеличить его температуру на один градус \(~C = \frac{\Delta Q}{\Delta t^\circ}\). Как видите, определение электроемкости полностью аналогично.

Можно дать аналогичное определение емкости сосуда: объем жидкости, который необходимо влить в сосуд, чтобы увеличит высоту его уровня на единицу, то придется признать, что емкость цилиндрического сосуда равна площади его дна \(~C = \frac{\Delta V}{\Delta h}\). В этом примере аналогом электрического заряда является объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости.

Электроемкость является размерной физической величиной. В системе единиц СИ единицей электроемкости является фарад (сокращенно Ф). Емкостью в 1 фарад обладает тело, потенциал которого возрастает на 1 вольт при увеличении его заряда на 1 кулон. Один фарад очень большая емкость, поэтому чаще используются дольные единицы: микрофарад (мкФ, 1 мкФ = 10^-6 Ф), нанофарад (нФ, 1 нФ = 10^-9 Ф), пикофарад (пФ, 1 пФ = 10^-12 Ф).

Для расчета электроемкости следует задать электрический заряд тела и рассчитать его потенциал, после чего вычислить их отношение. Так потенциал тела всегда пропорционален его заряду, то емкость тела не зависит от его заряда, а полностью определяется его размерами, формой и диэлектрическими свойствами среды, в которой находится тело.

Для примера найдем электрическую емкость уединенного шара радиуса R, находящегося в вакууме. Если заряд шара равен Q, то его потенциал (относительно бесконечности) равен

\(~\varphi = \frac{Q}{4 \pi \varepsilon_0 R}\) .

Следовательно, электрическая емкость шара равна

\(~C = \frac{Q}{\varphi} = 4 \pi \varepsilon_0 R\) . (3)

Так электрическая емкость земного шара (R ≈ 6350 км) равна С ≈ 7·10^-4 Ф - действительно 1 фарад очень большая емкость.

Если поместить шар в бесконечную среду из однородного диэлектрика с проницаемостью ε, то напряженность поля уменьшится в ε раз, потенциал шара также уменьшится, поэтому его емкость возрастет в ε раз:

\(~C = 4 \pi \varepsilon_0 \varepsilon R\) . (4)

16.1.2 Конденсаторы.

Мы показали, что уединенные тела малопригодны как накопители электрического заряда. Еще в середине XVIII века было изобретено устройство, способное накапливать и длительное время сохранять большие электрические заряды – конденсатор.

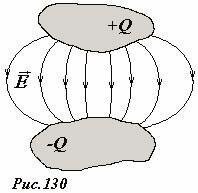
Конденсатор представляет собой два проводника (которые называются обкладками), разделенными диэлектриком (Рис. 130). Как правило, на обкладки подают разноименные электрические заряды, равные по величине. В этом случае электрическое поле практически полностью локализуется в пространстве между обкладками. Емкостью конденсатора называется отношение заряда одной из обкладок к разности потенциалов между обкладками

\(~C = \frac{\Delta Q}{\Delta \varphi}\) . (5)

В этом определении фигурирует разность потенциалов, которая не зависит от выбора нулевого уровня потенциала, поэтому нет необходимости в дополнительных оговорках. Часто зарядом конденсатора называют заряд одной из его обкладок (ясно, что полный заряд конденсатора на двух обкладках равен нулю), вместо разности потенциалов между обкладками чаще говорят о напряжении конденсатора U, которое, конечно, равно разности потенциалов U = Δϕ, так в пространстве между обкладками не действуют сторонние силы.

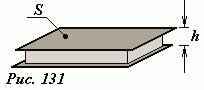
Простейший конденсатор состоит из двух проводящих параллельных пластин, разделенных слоем диэлектрика, причем расстояние между пластинами значительно меньше их размеров – такой конденсатор называется плоским (Рис. 131). Найдем емкость такого конденсатора. Будем считать, что на обкладки конденсатора (проводящие пластины) поданы разноименные электрические заряды, модули которых равны Q. Если площадь каждой пластины равна S , то поверхностная плотность заряда на них равна \(~\sigma = \frac{Q}{S}\). Эти заряды создают в пространстве между пластинами электрическое поле напряженности \(~E = \frac{\sigma}{\varepsilon \varepsilon_0} = \frac{Q}{\varepsilon \varepsilon_0 S}\), где ε - диэлектрическая проницаемость вещества между пластинами. Разность потенциалов между обкладками конденсатора равна \(~\Delta \varphi = Eh = \frac{Qh}{\varepsilon \varepsilon_0 S}\). По определению емкость плоского конденсатора рассчитывается по формуле

\(~C = \frac{Q}{\Delta \varphi} = \frac{\varepsilon \varepsilon_0 S}{h}\) . (6)

Таким образом, емкость конденсатора пропорциональна проницаемости диэлектрика, площади пластин и обратно пропорциональна расстоянию между ними. Если расстояние между пластинами сделать малым, а площади пластин большими, то такой конденсатор может иметь большую емкость (даже превосходящую емкость земного шара).

Конденсаторы широко используются не только для накопления электрического заряда, но и в цепях переменного электрического тока (эти вопросы мы рассмотрим позднее). На электрических схемах конденсаторы изображаются в виде двух параллельных отрезков (Рис. 132).

Промышленностью выпускаются конденсаторы различных типов, которые различаются своей конструкцией. Емкости промышленно выпускаемых конденсаторов изменяются в широких пределах от нескольких пикофарад, до единиц фарад. Часто пластины таких конденсаторов изготавливают из тонкой металлической фольги, которую скручивают в рулоны и помещают в корпус. В качестве диэлектрика используется воздух (в этом случае с высокой точностью можно считать ε = 1), слюда, сухая бумага, и другие материалы.

Большой электрической емкостью обладают электролитические конденсаторы. Одной обкладкой такого конденсатора служит тонкая полоска фольги большой площади, покрытая слоем окисла (который играет роль диэлектрика), второй обкладкой является раствор электролита. Так как толщина оксидного слоя может быть малой (порядка нескольких микрон), то емкость такого конденсатора весьма велика. При использовании таких конденсаторов следует внимательно следить за полярностью их включения в электрическую цепь, так как при ошибочном подключении оксидный слой быстро разрушается, что приводит к выходу конденсатора из строя.

Широко используются также конденсаторы переменной емкости, в котором наборы пластин могут двигаться друг относительно друга, при этом изменяется площадь их перекрытия, вследствие чего изменяется и емкость конденсатора. На схемах переменные конденсаторы отмечаются стрелкой (Рис. 132б).

16.1.3 Соединение конденсаторов.

Установим правила для расчета электроемкости системы конденсаторов, подобно правилам расчета сопротивлений соединенных резисторов.

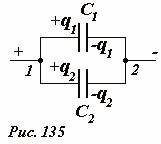
При параллельном соединении конденсаторов (Рис. 135) емкости которых равны C₁ и C₂ напряжения на обоих конденсаторах одинаковы и равны разности потенциалов между точками соединения U₁ = U₂ = Δϕ, что является следствием потенциальности электростатического поля. Суммарный заряд конденсатора равен сумме зарядов конденсаторов q = q₁ + q₂.

По определению емкость такого составного конденсатора равна отношению его суммарного заряда к напряжению, следовательно,

\(~C = \frac{q_1 + q_2}{U} = \frac{q_1}{U} + \frac{q_2}{U} = C_1 + C_2\) . (1)

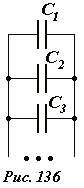
Это правило легко обобщается: общая емкость системы параллельно соединенных конденсаторов (Рис. 136) равна сумме емкостей всех конденсаторов

\(~C_o = C_1 + C_2 + C_3 + \ldots = \sum_k C_k\) . (2)

В частном случае плоских конденсаторов с одинаковыми расстояниями между пластинами установленное правило утверждает, что суммарная площадь пластин равна сумме площадей отдельных обкладок

\(~S_o = S_1 + S_2 + S_3 + \ldots\) .

При последовательном соединении конденсаторов (Рис. 137) суммарное напряжение на батарее конденсаторов равно сумме напряжений на отдельных конденсаторах

\(~U_o = U_1 + U_2\) . (3)

Электрические заряды на всех конденсаторах одинаковы

\(~q_o = q_1 = q_2\) .

Для доказательства этого утверждения достаточно рассмотреть две соединенных внутренних обкладки, которые изолированы от внешних источников – их суммарный заряд остается равным нулю. Поэтому если на обкладке первого конденсатора индуцируется заряд − q, то на соединенной с ней обкладке второго конденсатора возникнет такой же по модулю заряд противоположного знака.

Выразим напряжения на конденсаторах через их заряды и емкости \(~U = \frac{q}{C}\) и подставим их в уравнение (3)

\(~\frac{q_o}{C_o} = \frac{q_1}{C_1} + \frac{q_2}{C_2}\) ,

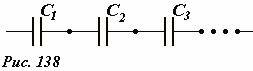
принимая во внимание равенство всех зарядов, получим правило расчета емкости последовательно соединенных конденсаторов (Рис. 138):

величина обратная емкости батареи последовательно соединенных конденсаторов равна сумме величин, обратных емкости каждого конденсатора,

\(~\frac{1}{C_o} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots = \sum_k \frac{1}{C_k}\) . (4)

Для плоских конденсаторов с одинаковыми площадями пластин это правило утверждает, что суммарное расстояние между пластинами равно сумме этих расстояний всех конденсаторов.

Интересно отметить, что правила расчетов емкости батареи конденсаторов противоположны правилам расчета сопротивлений соединений резисторов: при последовательном соединении складываются сопротивления; при параллельном – складываются величины обратные сопротивлениям (проводимости), а для конденсаторов наоборот: при параллельном соединении складываются емкости, а при последовательном – складываются обратные величины.

Примечания

Следующая страница