Слободянюк А.И. Физика 10/16.2
§16. Превращение энергии в электрических и магнитных явлениях
16.2 Математическое отступление.
Многие физические величины математически описываются как функции, которые могут зависеть от времени, координат и т.д. Большинство физических законов формулируются в виде уравнений, описывающих скорости изменения этих функций. Например, уравнение второго закона Ньютона описывает изменение скорости тела под действием внешних сил. К удовольствию физиков, различные физические процессы могут описываться одинаковыми уравнениями. Понятно, что одинаковые уравнения имеют одинаковые решения, что позволяет решения, полученные в одной области физики переносить на другие области. С математической точки зрения можно рассматривать решение этих уравнений, не оговаривая физический смысл входящих в него величин и параметров[1]. Сейчас мы познакомимся с одним из таких уравнений, очень часто встречающихся в различных областях физики.
Пусть скорость изменения некоторой физической величины, описываемой функцией X(t), пропорциональна самой величине, то есть подчиняется уравнению
где a - некоторая постоянная величина.
Параллельно с общим уравнением будем рассматривать конкретный физический пример. Пусть лодка массой m движется по поверхности воды, со стороны которой на тело действует тормозящая сила, пропорциональная скорости тела \(F = −\beta \upsilon\). В этом случае на основании второго закона Ньютона можно записать уравнение
Для однозначного определения функции X(t) уравнение (1) необходимо дополнить уравнение (1) начальным условием: значением функции X0 (для определенности будем считать, что X0 > 0) в момент времени t0 = 0.
В рассматриваемом физическом примере следует задать начальную скорость υ0.
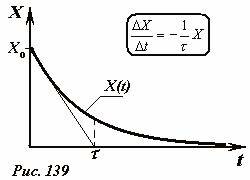
Качественно решение этого уравнения описывается следующим образом (Рис. 139): при t = 0 значение функции задается начальным условием X0, затем функция начинает убывать, причем сначала скорость убывания равна \(~\left (\frac{\Delta X}{\Delta t} \right )_{t = 0} = -a X_0\), по мере уменьшения значения функции X скорость ее убывания падает. Поэтому графиком этой функции будет монотонно убывающая кривая. Характерное время убывания функции оценивается как время, за которое функция стала бы равной нулю, если скорость ее убывания остается такой же, как в начальный момент времени
Таким образом, величина обратная коэффициенту пропорциональности в уравнении (1) имеет смысл характерного времени затухания, поэтому имеет смысл записать это уравнение в виде, явно включающем этот параметр
Теперь для определения характерного времени затухания, достаточно привести уравнение изменения к стандартному виду (3), в котором коэффициент пропорциональности имеет смысл величины, обратной времени затухания.
Точный смысл величины τ следующий[2]: за это время функция X убывает в e = 2,71828... раз.
Так непосредственно из вида уравнения (1а) следует, что характерное время движения лодки до остановки равно \(~\tau = \frac{m}{\beta}\).
Часто возникает необходимость в вычислении различных суммарных характеристик, описывающих весь процесс изменения X(t).
Вычислим некоторые из них.
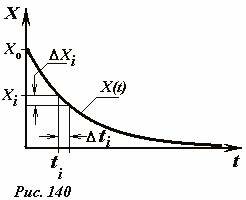
Пусть в некоторый момент времени ti значение рассматриваемой величины равно Xi , за последующий малый промежуток времени Δti величина X изменилась на малую величину ΔXi (Рис. 140).
Для вычисления суммы \(~\sum_i X_i \Delta t_i\) выразим значение функции через скорость ее изменения, после чего суммирование проводится элементарно
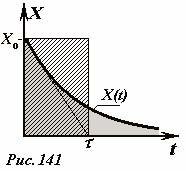
Полученная формула имеет наглядную геометрическую интерпретацию (Рис. 141): площадь под кривой затухания равна площади прямоугольника со сторонами X0 и τ.
Так применяя формулу (4) к движению лодки, получим, что сумма, имеющая смысл пути, пройденного до остановки, равна
Достаточно часто возникает необходимость в вычислении сумм вида \(~\sum_i X^2_i \Delta t_i\).
Выразим опять из уравнения (4) значение функции через скорость ее изменения \(~X_i = - \tau \frac{\Delta X_i}{\Delta t_i}\) и проведем суммирование
где Xk - значения величины в конце рассматриваемого промежутка времени. При выводе использовано соотношение, справедливое для малых изменений \(~\Delta (X^2) = 2 X \Delta X\) . Если суммирование проводится по всему процессу изменения величины X , то Xk = 0 и тогда
Работа сил сопротивления, действующих на лодку, за малый промежуток времени равна \(~\delta A = F \Delta x = - \beta \upsilon \cdot \upsilon \Delta t = - \beta \upsilon^2 \Delta t\). Для вычисления этой работы за все время торможения следует воспользоваться полученной формулой (5), тогда
Таким образом, ее модуль равен начальной кинетической энергии лодки, что является следствием закона сохранения энергии.
Теперь легко можно вычислить сумму \(~\sum_i \left (\frac{\Delta X_i}{\Delta t_i} \right )^2 \Delta t_i\) (с использованием уравнения (3)):
Обозначим, величину \(~\frac{\Delta X}{\Delta t} = V\) и получим уравнение для ее изменения. Для этого из уравнения (3), которое с учетом введенного обозначения, имеет вид \(~V = -\frac{1}{\tau} X\), перейдем к уравнению для малых изменений \(~\Delta V = -\frac{1}{\tau} \Delta X\) и разделим его на интервал времени \(~\frac{\Delta V}{\Delta t} = -\frac{1}{\tau} \frac{\Delta X}{\Delta t}\). Таким образом, мы получаем интересный результат: если некоторая величина X подчиняется уравнению (3), то скорость ее изменения подчиняется такому же уравнению
Из этого уравнения запишем \(~\Delta V = -\frac{1}{\tau} V \Delta t = -\frac{1}{\tau} \Delta X\). Из этого соотношения следует, что отношение изменения скорости к изменению самой величина есть величина постоянная
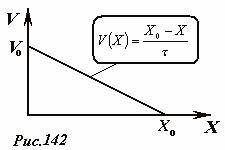
поэтому зависимость скорости от самой величины линейна
есть отрезок прямой линии (Рис. 142).
Рассмотрим теперь поведение функции X(t), изменение которой подчиняется уравнению
Преобразуем это уравнение к виду
Если функция \(~X = \overline{X} = \frac{b}{a}\), то скорость ее изменения равна нулю, поэтому это значение не будет изменяться с течением времени, оно является стационарным. Обозначим отклонение функции от ее стационарного значения \(~\left ( X - \frac{b}{a} \right ) = Y\). Для этого отклонения справедливо уравнение
только что изученное нами. Для него справедливы все полученные выводы.
Уравнение (10) лучше переписать в виде
в котором все параметры имеют явный смысл\[~\overline{X} = \frac{b}{a}\] - стационарное (равновесное) значение функции, к которому стремится решение уравнения (12) не зависимо от начального значения; \(~\tau = \frac{1}{a}\) - характерное время перехода к стационарному значению.
Задание для самостоятельной работы.
- Рассмотрите движение лодки под действием постоянной силы тяги и силы сопротивления, пропорциональной скорости. Покажите, что это движение описывается уравнением вида (12), определите параметры этого уравнения. Качественно проанализируйте решение этого уравнения.