Решение. Сила упругости. B16

Условие

B16. Постройте график зависимости силы упругости, возникающей в деформированной пружине F_упр = f(Δl), от ее удлинения, если жесткость пружины 200 Н/м.

Решение

Уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения F_упр = k∙Δl, где k = 200 Н/м. Тогда уравнение примет вид F_упр = 200∙Δl. Это линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.

Таблица значений данной функции имеет вид:

Fупр, Н	0
Δl, см	0

Для заполнения таблицы выбираем произвольные значения удлинения. Пусть, например, Δl = 5 см = 5∙10^-2 м. Получаем F_упр(5∙10^-2 м) = 200 ∙ 5∙10^-2 = 10 (Н). Подставляем эти значения в таблицу:

Fупр, Н	0	10
Δl, см	0	5

По оси ординат откладывают значения функции (F_упр), по оси абсцисс – аргумента (Δl). На осях укажем обозначения и через запятую единицы соответствующих физических величин.

Масштаб графика определяется абсолютными погрешностями тех величин, которые откладываются по осям. Так как в нашем случае погрешность не определена, то при выборе масштаба будем следить, чтобы наши значения не вышли за границы осей, а с другой стороны, график не должен быть очень мелким. Можно сделать так, максимальное значение на графике сделать равным максимальному значению величин в таблицах.

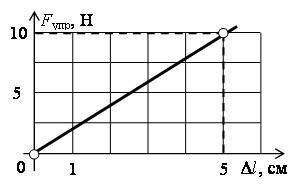
Отметим полученные точки и соедините их прямой линией. Полученный график изображен на рис. 1.

Рис. 1