Слободянюк А.И. Физика 10/12.2
§12. Постоянное магнитное поле
12.2 Вектор индукции магнитного поля.
Прежде чем дать строгое определение характеристик магнитного поля нам необходимо сделать небольшое физико-математическое отступление, что бы познакомиться с еще одной операцией над векторами – векторным произведением.
12.2.1 Вектор угловой скорости; векторное произведение.
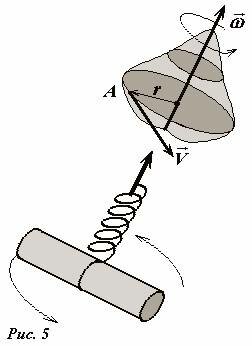
Рассмотрим еще раз вращательное движение твердого тела. Чтобы однозначно задать кинематические характеристики такого движения необходимо указать ось вращения и величину угловой скорости (Рис.5). Фактически, как и в случае поступательного движения, необходимо указать величину и направление, что удобно сделать в единой векторной форме. Определим [1] угловую скорость как вектор, величина которого численно равна угловой скорости, b направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось [2], что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен.
Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») - если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.
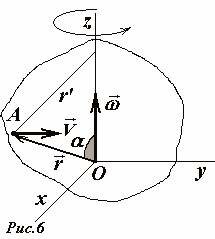
Посмотрим, как можно теперь найти линейную скорость произвольной точки A вращающегося тела, находящейся на расстоянии r от оси вращения. Тогда модуль скорости точки A будет равен \(V_A = \omega r\). Направлен этот вектор перпендикулярно плоскости, проходящей через ось вращения и рассматриваемую точку.
Введем теперь систему координат, начало которой, точка O, находится на оси вращения (Рис.6). Тогда положение произвольной точки A задается радиус-вектором \(~\vec r\) , соединяющим начало отсчета с выбранной точкой. Модуль скорости этой точки можно рассчитать по формуле
где \(r' = r \sin \alpha\) - расстояние до оси вращения, α - угол между векторами \(~\vec \omega\) и \(~\vec r\). Направлен вектор скорости \(~\vec V\) перпендикулярно плоскости, проходящей через векторы \(~\vec \omega\) и \(~\vec r\). Так давайте, определим новую математическую операцию над векторами \(~\vec \omega\) и \(~\vec r\), такую, чтобы ее результатом был вектор \(~\vec V\).
Естественно, что такая операция была придумана до нас и называется она векторным произведением
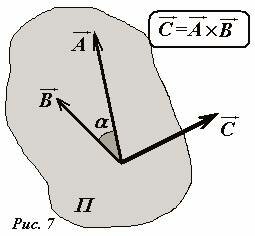
Определение. Векторным произведением двух векторов \(~\vec A\) и \(~\vec B\), называется вектор \(~\vec C = \vec A \times \vec B\) , модуль которого равен
где α - угол между векторами-сомножителями \(~\vec A\) и \(~\vec B\), отсчитываемый от первого сомножителя ко второму; направлен вектор произведения перпендикулярно каждому из векторов-сомножителей в такую сторону, чтобы кратчайший поворот, от первого сомножителя \(~\vec A\) ко второму \(~\vec B\) проходил против часовой стрелки, если смотреть с конца вектора \(~\vec C\).
Отметим, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах-сомножителях.
Для того чтобы найти результат векторного произведения \(~\vec C = \vec A \times \vec B\) произвольных векторов \(~\vec A\) и \(~\vec B\) по определению необходимо проделать следующее (Рис. 7):
- построить плоскость, проходящую через векторы сомножители \(~\vec A\) и \(~\vec B\);
- восстановить перпендикуляр к этой плоскости (вектор произведения направлен вдоль этого перпендикуляра);
- Выбрать такое направление вектора \(~\vec C\), чтобы ближайший поворот от первого сомножителя \(~\vec A\) ко второму \(~\vec B\) проходил против часовой стрелки;
- Рассчитать длину (модуль) вектора произведения по формуле (3).
Направление вектора произведения также можно определять по правилу правого винта: если вращать ручку буравчика от первого сомножителя ко второму, то направление его движения укажет направление вектора произведения.
Задание для самостоятельной работы.
- Проверьте, пользуясь определением векторного произведения, справедливость формулы (2), связывающей линейную и угловую скорости точки.
Укажем также некоторые свойства векторного произведения, которые легко доказать, исходя из определения.
- При изменении порядка сомножителей направление произведения изменяется на противоположное \(~\vec A \times \vec B = -\vec B \times \vec A\) .
- Обратите на это свойство особое внимание, наверно, вы впервые вы встречаетесь с ситуацией, когда «от перемены мест сомножителей произведение… меняется!», поэтому при выполнении операций, включающих векторное произведение, необходимо тщательно следить за порядком следования сомножителей. Можно также сказать, что для векторного произведения не выполняется коммутативный закон.
- Для векторного произведения справедлив ассоциативный закон
-
\(~\vec A \times (\vec B + \vec C) = \vec A \times \vec B + \vec A \times \vec C\) . (4)
-
12.2.2 Вектор момента силы - векторное произведение.
Рассмотрим теперь понятие вектора момента силы. Ранее мы определили момент силы, как произведение момента силы на ее плечо. Покажем, что момент силы может быть описан как вектор и представлен в виде векторного произведения.
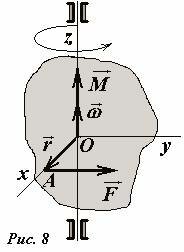
Пусть произвольное твердое тело может вращаться вокруг фиксированной оси, с которой совместим ось Oz декартовой системы координат (Рис.8). Пусть сила \(~\vec F\) приложена к точке A, расположенной на оси Ox, на расстоянии r от оси вращения (положение этой точки задается радиус-вектором \(~\vec r\)) и направлена перпендикулярно оси Ox. Действие этой силы приведет к вращению тела вокруг оси, которое может быть описано вектором угловой скорости \(~\vec \omega\), направленным вдоль оси вращения. Разумно определить вектор момента силы так, чтобы он был направлен тоже вдоль оси вращения [3]. В нашем случае модуль вектора момента силы равен произведению \(M = rF\), можно заметить, «правильное» направление этого вектора будет задано, если определить его как векторное произведение
Эта формула дает самое строгое определение вектора момента силы. Проверьте самостоятельно, что для произвольного вектора силы, лежащего в плоскости xOy, формула (5) дает вектор момента силы, направленный вдоль оси вращения, модуль которого соответствует данному ранее определению.
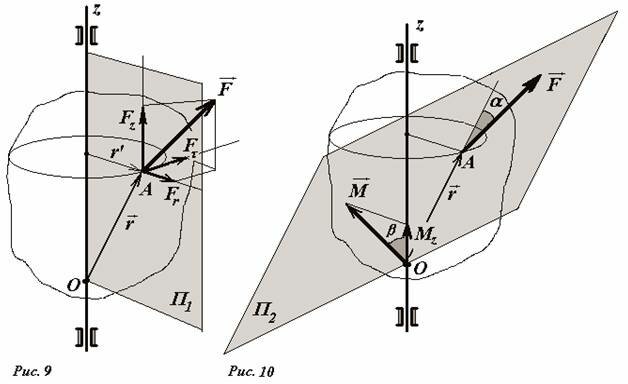
Наконец, рассмотрим более общий случай: пусть произвольное тело может вращаться вокруг фиксированной оси Oz, приложенная сила \(~\vec F\) направлена произвольно и приложена к произвольной точке A с радиус-вектором \(~\vec r\) (Рис.9).
Если ось вращения фиксирована, то тело может вращаться только вокруг этой оси. Проведем через точку приложения силы A окружность с центром на оси вращения, плоскость которой перпендикулярна этой оси. Разложим вектор силы на следующие составляющие: осевую Fz - вдоль оси вращения; радиальную Fr - вдоль радиуса построенной окружности; тангенциальную Fτ - вдоль касательной к построенной окружности. Каждая из этих составляющих имеет наглядный и очевидный физический смысл: Осевая составляющая стремится сдвинуть тело вдоль оси, если тело закреплено, она должна быть уравновешена силами реакции в опорах оси; радиальная составляющая стремится сдвинуть тело в перпендикулярном направлении (или изогнуть ось), она также компенсируется силами реакции; и только тангенциальная составляющая способна придать вращение телу. Поэтому момент силы, который приводит к вращению тела, определяется как произведение тангенциальной составляющей силы на расстояние от оси вращения до точки приложения силы
Найдем теперь вектор момента силы по данному выше определению (5). В соответствии с определением операции векторного произведения построим плоскость (Рис. 10), проходящую через векторы \(~\vec r\) и \(~\vec F\), и восстановим перпендикуляр к ней, который (с учетом правила буравчика) укажет направление вектора \(~\vec M = \vec r \times \vec F\). Модуль этого вектора равен \(~|\vec M| = r F \sin \alpha\) , где α - угол между векторами \(~\vec r\) и \(~\vec F\). В общем случае направление вектора момента силы не совпадает с направлением оси вращения.
Однако не следует забывать, что на тело помимо рассматриваемой силы \(~\vec F\), действуют силы реакции в опорах оси, моменты которых отличны от нуля [4]. Поэтому при рассмотрении вращения тела вокруг фиксированной оси нас интересует только проекция вектора \(~\vec M = \vec r \times \vec F\) на ось вращения. Следовательно, можно утверждать, что момент силы, приводящий к вращению тела, рассчитывается по формуле
где β - угол между вектором момента силы и осью вращения.
Остальные проекции вектора момента силы компенсируются моментами сил реакции.
Для расчета вектора момента силы можно также воспользоваться разложением вектора силы на составляющие
В этом выражение первые два слагаемых являются векторами, перпендикулярными оси вращения, поэтому не могут привести к вращению тела, и только последнее слагаемое имеет составляющую, направленную вдоль оси вращения.
Задание для самостоятельной работы.
- В качестве хорошего упражнения по стереометрии докажите, что формулы (6) и (7) эквивалентны.
12.2.3 Вектор индукции магнитного поля.
Вспомним, электрическое поле действует с некоторой силой \(~\vec F\) на неподвижный электрический заряд, величина этой силы пропорциональна величине заряда q, поэтому отношение силы, действующей на электрический заряд к его величине, не зависит от свойств заряда, следовательно, является характеристикой, электрического поля – его напряженностью \(~\vec E = \frac{\vec F}{q}\) . В этом случае пробный заряд фактически выступает в роли прибора для обнаружения поля и измерения его характеристик.
Магнитное поле действует на движущиеся заряды, следовательно, и характеристика этого поля должна быть связана с этой силой. Но движущийся заряд описывается не только величиной заряда, но и вектором скорости, следовательно, и сила, действующая на этот заряд, зависит также от вектора его скорости. Поэтому движущийся пробный заряд, как прибор для обнаружения магнитного поля не обладает сферической симметрией (как неподвижный точечный заряд), следовательно, характеристика магнитного поля не может быть определена так же просто как напряженность электрического поля [5].
Практически более удобно в качестве «пробного» прибора для изучения магнитного поля использовать малый проводящий контур с электрическим током [6], поведение которого в магнитном поле аналогично поведению намагниченной стрелки.
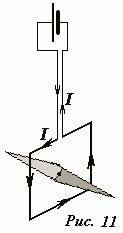
Вспомним, что для создания постоянного тока в замкнутом контуре необходим источник ЭДС, тем не менее, можно реально создать малый контур с постоянным током. Для этого достаточно подвесить проводящую рамку на двух тонких проводах, подключенных к источнику (рис.11). Так как в подводящих проводах токи текут в противоположных направлениях, то суммарный ток равен нулю. Как было установлено Эрстедом и подтверждено А. Ампером в магнитном поле контур с током стремится занять определенную ориентацию в пространстве, стремится повернуться, следовательно, со стороны магнитного поля на контур (как и на стрелку) действует вращающий момент сил. Момент сил (а не сила, как в случае электрического поля), действующих на контур, служит для определения характеристики магнитного поля.
Опыт показывает, что момент сил, действующих на контур, зависит от его ориентации в пространстве, следовательно, физическая величина, описывающее магнитное поле, должна быть векторной. В общем случае этот вектор может изменяться от точки к точке, поэтому магнитное поле должно описываться математически как уже знакомое нам векторной поле.
Так как мы хотим определить «точечную» характеристику магнитного поля, то такой контур (или магнитную стрелку) следует считать бесконечно малым.
В очередной раз мы должны сделать традиционную оговорку – бесконечно малый контур физически нереализуем – даже провода имеют конечную толщину, поэтому переход к бесконечно малому контуру следует понимать в физическом смысле – мал, настолько, что с математической точки можно считать бесконечно малым, но реально реализуемым.
Чтобы избавиться от неоднозначности измеряемого момента сил, связанной с ориентацией контура, выберем такое положение контура, при котором модель момента сил максимален Mmax. Наконец, учтем еще один экспериментальный факт – момент сил, действующих на контур, пропорционален силе тока в контуре I и площади контура S.
Следовательно, отношение момента сил к произведению силы тока в контуре на его площадь является величиной, не зависящей от свойств контура, поэтому является характеристикой поля, которая называется индукцией магнитного поля
Теперь необходимо определиться с направлением вектора индукции магнитного поля. Наиболее наглядно направление этого вектора в данной точке указывает северный полюс магнитной стрелки в состоянии устойчивого равновесия. Свяжем теперь это направление с ориентацией контура с током, который мы выбрали в качестве индикатора поля. Для этого введем еще одну характеристику контура – его магнитный момент [7].
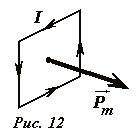
Магнитными моментом контура (рис. 12) называется вектор направленный перпендикулярно плоскости контура, модуль которого равен произведению силы тока в контуре на его площадь \(p_m = IS\) . Направление этого вектора определяется по правилу правого винта – если направление тока совпадает с направлением вращения винта, то направление движения последнего совпадает с направлением вектора магнитного момента. Если смотреть с конца вектора момента, то направление обхода контура по направлению тока положительной, то есть против часовой стрелки.
Таким образом, направление вектора индукции магнитного поля совпадает с направлением вектора магнитного момента контура, помещенного в данную точку поля и находящегося в положении устойчивого равновесия.
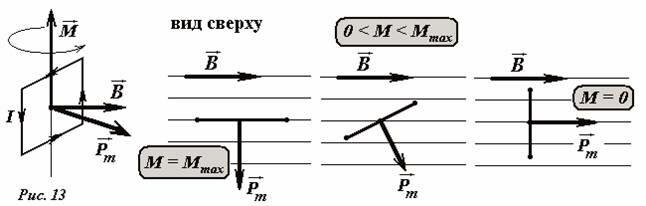
Еще раз рассмотрим ориентации векторов, которые задействованы в определении вектора индукции магнитного поля. Пусть в некоторой области пространства магнитное поле можно считать однородным (то есть вектор индукции во всех точках постоянен, как по величине, так и по направлению). Будем также считать, что ось вращения контура перпендикулярна направлению вектора индукции магнитного поля (Рис.13). Вектор момента сил \(~\vec M\) перпендикулярен вектору магнитной индукции \(~\vec B\) и вектору магнитного момента контура \(~\vec p_m\). На контур будет действовать со стороны магнитного поля максимальный момент сил в том случае, когда эти векторы перпендикулярны (то есть вектор индукции поля лежит в плоскости контура), а в положении равновесия вектор индукции перпендикулярен плоскости контура.
Наконец, запишем общее выражение для момента силы, действующего на контур с током со стороны магнитного поля, воспользовавшись операцией векторного произведения
Простота этой формулы оправдывает все наши долгие рассуждения по определению характеристики магнитного поля. Фактически эта формула может рассматриваться как определение вектора индукции магнитного поля.
Сравните с выражением для силы, действующей со стороны электрического поля на точечный заряд \(~\vec F = q \vec E\) . Похоже: q - характеристика индикатора электрического поля, \(~\vec p_m\) - характеристика индикатора магнитного поля; \(~\vec E\) - основная характеристика электрического поля, \(~\vec B\) - основная характеристика магнитного поля; \(~\vec F\) - результат воздействия электрического поля на точечный заряд, \(~\vec M\) - результат воздействия магнитного поля на контур.
Индукция магнитного поля является размерной физической величиной. В системе СИ единицей измерения индукции является Тесла (сокращенно Тл), названная в честь американского (югославского происхождения) физика и инженера Николы Тесла. Эта единица является производной, она может быть выражена через другие единицы с помощью формулы (8):
Примечания
- ↑ Именно дадим определение, потому, что все физические величины «придуманы» человеком, реально же существует движущееся тело, а как мы его описываем – дело нашего воображения. Раньше мы обходились без векторного описания, да и векторное исчисление придумано значительно позже, чем была создана механика, даже Дж. К. Максвелл «не знал» векторов!
- ↑ Может, в те времена часы ходили в другую сторону?
- ↑ Данное высказывание не совсем точно: более строго следует говорить, что вектор момента силы указывает направление изменения вектора угловой скорости, то есть совпадает с направлением вектора угловой скорости. Однако, в рассматриваемом здесь случае все три вектора момента силы, угловой скорости и углового ускорения направлены вдоль одной оси - фиксированной оси вращения.
- ↑ Обратите внимание: чуть выше мы говорили, что некоторые компоненты вектора силы компенсируются силами реакции; сейчас утверждаем, что некоторые компоненты вектора момента силы компенсируются моментами сил реакций. Эти высказывания не противоречат друг другу: кому-то больше нравятся силы, а кому-то их моменты – реально же вращение тела вокруг закрепленной оси, а описывать его можно по-разному.
- ↑ Хотя бы потому, что операция деления вектора на вектор не определена.
- ↑ Может быть, магнитная стрелка в качестве пробного прибора и более наглядна, но физические характеристики контура с током легче задать и определить.
- ↑ В некотором смысле она аналогична дипольному моменту в электростатике. Магнитная стрелка компаса, некоторые атомы и молекулы, такие элементарные частицы как электрон, протон, нейтрон обладают собственными магнитными моментами, хотя говорить об их площади, или силе тока говорить не приходится.