Слободянюк А.И. Физика 10/13.6
§13. Взаимодействие магнитного поля с веществом
13.6 Взаимодействие магнетиков с постоянным магнитным полем.
Под действием внешнего магнитного поля любое вещество намагничивается. Как мы показали, намагничивание тела может быть заменено эквивалентной системой токов. Поэтому расчет силы, действующей на произвольное тело со стороны внешнего магнитного поля, может быть проведен по методике, аналогичной расчету сил взаимодействия постоянных магнитов, которую следует дополнить расчетом индуцированного магнитного момента тела.
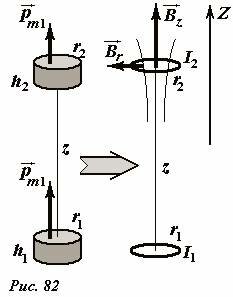
Проиллюстрируем эти расчеты на простейшем примере: в рассмотренной выше задаче заменим второй постоянный магнит цилиндром из первоначально не намагниченного материала (Рис. 82). Если размеры этого тела малы, то при расчете его намагниченности можно пренебречь неоднородностью внешнего магнитного поля, создаваемого постоянным магнитом, то есть считать, что намагниченность полностью определяется осевой составляющей поля. Поэтому для неферромагнитных материалов[1] намагниченность цилиндра равна
здесь (μ −1)= χ - магнитная восприимчивость вещества цилиндра, поэтому его индуцированный магнитный момент равен
Положительным направлением магнита здесь, как и ранее принято направление магнитного момента постоянного магнита, или направление внешнего магнитного поля, в котором находится рассматриваемое тело. Формула (2) явно указывает, что парамагнетики (μ > 1) намагничиваются «по полю» - для них магнитный момент положительный, а диамагнетики (μ < 1) намагничиваются «против поля», их магнитный момент отрицательный. Используя формулы (1)-(4) из предыдущего раздела, получим выражение для силы, действующей на цилиндр
Эта формула справедлива для любого осесимметричного внешнего поля, так как мы нигде не использовали конкретных формул для индукции этого поля. Как и в случае постоянного магнита, сила, действующая на тело со стороны магнитного поля, зависит от скорости изменения этого поля \(~\frac{\Delta B_z}{\Delta z}\), следовательно, в однородном поле эта сила равна нулю. Преобразуем формулу (3) с учетом равенства, которое мы неоднократно использовали ранее \(~B_z \Delta B_z = \Delta \left (\frac{B^2_z}{2} \right )\) :
Эта формула показывает, что направление силы, действующей на магнетик со стороны магнитного поля, определяется не правлением вектора индукции, а направлением изменения его квадрата, а модуль этой силы пропорционален скорости изменения квадрата индукции поля. Хорошо известно и легко показать, что северный полюс постоянного магнита притягивает кусочек не намагниченного железа точно также как и его южный полюс. Таким образом, парамагнетики (μ > 1) втягиваются в ту область, где модуль напряженности больше, а диамагнетики (μ < 1) выталкиваются из области более сильного поля. Если необходимо увеличить силу, действующую на тело (как, например, в кранах с электромагнитом), необходимо не только увеличивать индукцию поля, но и стремиться сделать его более неоднородным.
Перепишем еще раз формулу (4), представив ее в виде
в дальнейшем мы покажем, что величина \(~\frac{B^2_z}{2 \mu_0}\) является плотностью энергии магнитного поля, поэтому направление силы определяется направлением изменения плотности энергии магнитного поля.
Закончим расчет силы взаимодействия постоянного магнита и не намагниченного цилиндра, для чего в формулу (3) подставим выражения для осевой и радиальной составляющих индукции поля постоянного магнита
В данном случае сила взаимодействия убывает очень резко с возрастанием расстояния между взаимодействующими телами – обратно пропорционально седьмой степени расстояния, то есть при увеличении расстояния в 2 раза сила взаимодействия уменьшается в 128 раз.
Напомним, что формула (5) применима в случае, когда расстояние между взаимодействующими телами значительно превышает их размеры. В общем случае расчет силы взаимодействия значительно усложняется, хотя основной качественный вывод остается справедливым: сила взаимодействия пропорциональна магнитной восприимчивости вещества и зависит не только от величины индукции поля, но и от скорости ее изменения в пространстве.
Примечания
- ↑ эти рассуждения применимы и для ферромагнетиков намагниченность которых далека от насыщения.